计算机系统与云计算(转载) 浮点数
http://cenalulu.github.io/linux/about-denormalized-float-number/
一个有趣的实验
本文从一个有趣而诡异的实验开始。最早这个例子博主是从 Stackoverflow上的一个问题中看到的。为了提高可读性,博主这里做了改写,简化成了以下两段代码:
#include <iostream>
#include <string>
using namespace std;
int main() {
const float x=1.1;
const float z=1.123;
float y=x;
for(int j=0;j<90000000;j++)
{
y*=x;
y/=z;
y+=0.1f;
y-=0.1f;
}
return 0;
}#include <iostream>
#include <string>
using namespace std;
int main() {
const float x=1.1;
const float z=1.123;
float y=x;
for(int j=0;j<90000000;j++)
{
y*=x;
y/=z;
y+=0;
y-=0;
}
return 0;
}上面两段代码的唯一差别就是第一段代码中y+=0.1f,而第二段代码中是y+=0。由于y会先加后减同样一个数值,照理说这两段代码的作用和效率应该是完全一样的,当然也是没有任何逻辑意义的。假设现在我告诉你:其中一段代码的效率要比另一段慢7倍。想必读者会认为一定是y+=0.1f的那段慢,毕竟它和y+=0相比看上去要多一些运算。但是,实验结果,却出乎意料, y+=0的那段代码比y+=0.1f足足慢了7倍。{: style="color: red" } 。世界观被颠覆了有木有?博主是在自己的Macbook Pro上进行的测试,有兴趣的读者也可以在自己的笔记本上试试。(只要是支持SSE2指令集的CPU都会有相似的结果)。
shell> g++ code1.c -o test1
shell> g++ code2.c -o test2
shell> time ./test1
real 0m1.490s
user 0m1.483s
sys 0m0.003s
shell> time ./test2
real 0m9.895s
user 0m9.871s
sys 0m0.009s
当然 原文中的投票最高的回答解释的非常好,但博主第一次看的时候是一头雾水,因为大部分基础知识已经还给大学老师了。所以,本着知其然还要知其所以然的态度,博主做了一个详尽的分析和思路整理过程。也希望读者能够从0开始解释这个诡异现象的原因。
复习浮点数的二进制转换
现在让我们复习大学计算机基础课程。如果你熟练掌握了浮点数向二进制表达式转换的方法,那么你可以跳过这节。
我们先来看下浮点数二进制表达的三个组成部分。
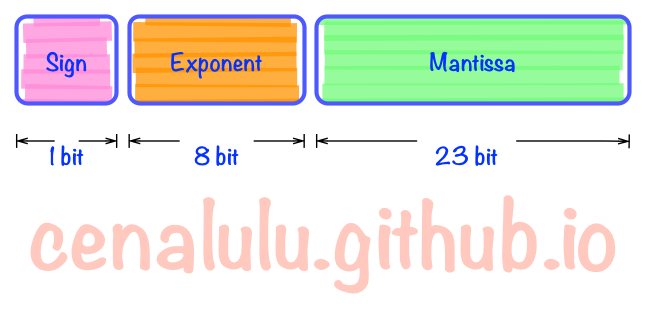
三个主要成分是:
- Sign(1bit):表示浮点数是正数还是负数。0表示正数,1表示负数
- Exponent(8bits):指数部分。类似于科学技术法中的
M*10^N中的N,只不过这里是以2为底数而不是10。需要注意的是,这部分中是以2^7-1即127,也即01111111代表2^0,转换时需要根据127作偏移调整。 - Mantissa(23bits):基数部分。浮点数具体数值的实际表示。
下面我们来看个实际例子来解释下转换过程。
Step 1 改写整数部分
以数值5.2为例。先不考虑指数部分,我们先单纯的将十进制数改写成二进制。
整数部分很简单,5.即101.。
Step 2 改写小数部分
小数部分我们相当于拆成是2^-1一直到2^-N的和。例如:0.2 = 0.125+0.0625+0.007825+0.00390625即2^-3+2^-4+2^-7+2^-8....,也即.00110011001100110011
Step 3 规格化
现在我们已经有了这么一串二进制101.00110011001100110011。然后我们要将它规格化,也叫Normalize。其实原理很简单就是保证小数点前只有一个bit。于是我们就得到了以下表示:1.0100110011001100110011 * 2^2。到此为止我们已经把改写工作完成,接下来就是要把bit填充到三个组成部分中去了。
Step 4 填充
指数部分(Exponent):之前说过需要以127作为偏移量调整。因此2的2次方,指数部分偏移成2+127即129,表示成10000001填入。
整数部分(Mantissa):除了简单的填入外,需要特别解释的地方是1.010011中的整数部分1在填充时被舍去了。因为规格化后的数值整部部分总是为1。那大家可能有疑问了,省略整数部分后岂不是1.010011和0.010011就混淆了么?其实并不会,如果你仔细看下后者:会发现他并不是一个规格化的二进制,可以改写成1.0011 * 2^-2。所以省略小数点前的一个bit不会造成任何两个浮点数的混淆。
具体填充后的结果见下图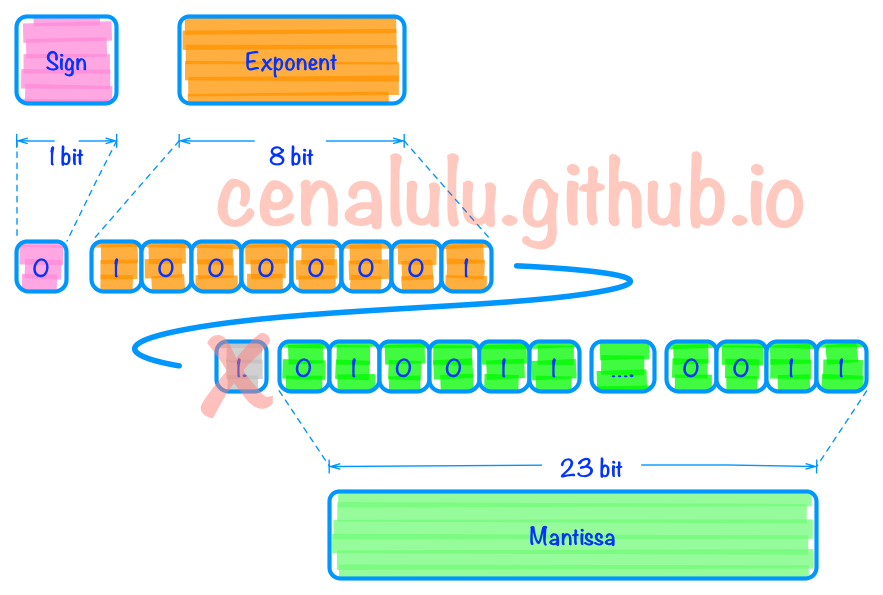
练习:如果想考验自己是否充分理解这节内容的话,可以随便写一个浮点数尝试转换。通过 浮点二进制转换工具可以验证答案。
什么是Denormalized Number
了解完浮点数的表达以后,不难看出浮点数的精度和指数范围有很大关系。最低不能低过2^-7-1最高不能高过2^8-1(其中剔除了指数部分全0喝全1的特殊情况)。那么当我们要表示一个例如:1.00001111*2^-7这样的超小数值的时候就无法用规格化数值表示,只能用0来代替。那么,这样做有什么问题呢?最容易理解的一种副作用就是:当多次做低精度浮点数舍弃的时候,就会出现除数为0的exception,导致异常。
于是乎就出现了Denormalized Number(后称非规格化浮点)。他和规格浮点的区别在于,规格浮点约定小数点前一位默认是1。而非规格浮点约定小数点前一位可以为0,这样小数精度就相当于多了最多2^22范围。
但是,精度的提升是有代价的。由于CPU硬件只支持,或者默认对一个32bit的二进制使用规格化解码。因此需要支持32bit非规格数值的转码和计算的话,需要额外的编码标识,也就是需要额外的硬件或者软件层面的支持。以下是wiki上的两端摘抄,说明了非规格化计算的效率非常低。> 一般来说,由软件对非规格化浮点数进行处理将带来极大的性能损失,而由硬件处理的情况会稍好一些,但在多数现代处理器上这样的操作仍是缓慢的。极端情况下,规格化浮点数操作可能比硬件支持的非规格化浮点数操作快100倍。
For example when using NVIDIA's CUDA platform, on gaming cards, calculations with double precision take 3 to 24 times longer to complete than calculations using single precision.
如果要解释为什么有如此大的性能损耗,那就要需要涉及电路设计了,超出了博主的知识范围。当然万能的wiki也是有答案的,有兴趣的读者可以自行查阅。
回到实验
总上面的分析中我们得出了以下结论:
- 浮点数表示范围有限,精度受限于指数和底数部分的长度,超过精度的小数部分将会被舍弃(underflow)
- 为了表示更高精度的浮点数,出现了非规格化浮点数,但是他的计算成本非常高。
于是我们就可以发现通过几十上百次的循环后,y中存放的数值无限接近于零。CPU将他表示为精度更高的非规格化浮点。而当y+0.1f时为了保留跟重要的底数部分,之后无限接近0(也即y之前存的数值)被舍弃,当y-0.1f后,y又退化为了规格化浮点数。并且之后的每次y*x和y/z时,CPU都执行的是规划化浮点运算。
而当y+0,由于加上0值后的y仍然可以被表示为非规格化浮点,因此整个循环的四次运算中CPU都会使用非规格浮点计算,效率就大大降低了。
其他
当然,也有在程序内部也是有办法控制非规范化浮点的使用的。在相关程序的上下文中加上fesetenv(FE_DFL_DISABLE_SSE_DENORMS_ENV);就可以迫使CPU放弃使用非规范化浮点计算,提高性能。我们用这种办法修改上面实验中的代码后,y+=0的效率就和y+=0.1f就一样了。甚至还比y+=0.1f更快了些,世界观又端正了不是么:) 修改后的代码如下
#include <iostream>
#include <string>
#include <fenv.h>
using namespace std;
int main() {
fesetenv(FE_DFL_DISABLE_SSE_DENORMS_ENV);
const float x=1.1;
const float z=1.123;
float y=x;
for(int j=0;j<90000000;j++)
{
y*=x;
y/=z;
y+=0;
y-=0;
}
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号