[机房测试]巨神兵

Description

求一个 \(n\leq 17\) 个点 \(m\) 条边的有向图有多少个边的子集不包含环。

Solution

边很多，只能对点状压。考虑一个 DAG 可以被怎么构造。假设 \(S\) 已经是一个拓扑图，那么加上一点集 \(T\)，如果只从 \(S\) 向 \(T\) 连边，那么构造出的图一定也还是拓扑图。所以就可以有转移

\[f_{S|T} \gets f_S \times 2^{cnt} \]

\(cnt\) 表示 \(S\) 到 \(T\) 的有向边个数。但是这样会算重。我们考虑一个特定方案被计算了几次。

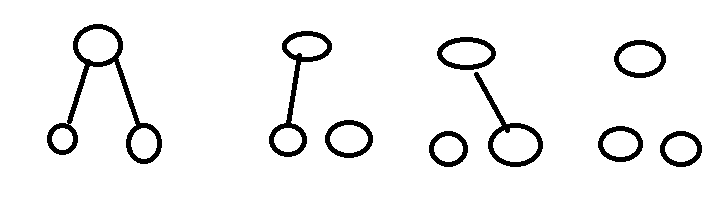
例如，左边的方案可以从右边三种状态分别转移一次。扩展到更多的点，容易发现会被重复计算 \(2^{c}-1\) 次。\(c\) 是该种特定方案最下面一层的点（没有出度的点）的个数。考虑容斥掉，我们只需要保留一次贡献。容易发现这个 \(2^{c}\) 其实是二项式定理得来的，对于所有有 \(k\) 个出度为零的点在 \(S\) 里面的方案，总共就会产生 \(\binom{c}{k}\) 的贡献，而出度为零的点不可能全部在 \(S\) 里面，所以总共只会有 \(2^c-1\) 次。所以只需要对每个 \(T\) 对 \(S|T\) 的贡献乘上 \((-1)^{|T|+1}\) 的容斥系数，就可以把中间的二项式全部抵掉。

#include<stdio.h>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;

inline int read(){
    int x=0,flag=1; char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')flag=0;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+c-48;c=getchar();}
    return flag? x:-x;
}

const int N=17;
const int Mod=1e9+7;

int mp[N][N],g[1<<N],in[1<<N],op[1<<N],pw[N*N],f[1<<N];

int main(){
    freopen("obelisk.in","r",stdin);
    freopen("obelisk.out","w",stdout);
    int n=read(),m=read(); pw[0]=f[0]=1;
    for(int i=1;i<=m;i++){
        int u=read(),v=read();
        mp[u-1][v-1]=1,pw[i]=2ll*pw[i-1];
    }
    int rg=(1<<n); op[0]=-1;
    for(int i=1;i<rg;i++) op[i]=-op[i-(-i&i)];
    for(int S=0;S<rg-1;S++){
        for(int i=0;i<n;i++) in[1<<i]=0;
        for(int i=0;i<n;i++){
            if(!((S>>i)&1)) continue;
            for(int j=0;j<n;j++) in[1<<j]+=mp[i][j];
        }
        const int U=rg-S-1; g[0]=0;
        for(int s=U&(U-1);;s=U&(s-1)){
            const int now=U^s;
            g[now]=g[now-(-now&now)]+in[-now&now];
            f[now^S]=(f[now^S]+1ll*f[S]*pw[g[now]]*op[now]%Mod+Mod)%Mod;
            if(!s) break;
        }
    }
    printf("%d",f[rg-1]);
}