[SCOI2005]最大子矩阵

Link

Solution

记得很早以前就看了这道题了，当时不会做就一直没做。后来发现 \(m\leq 2\)，我也是服了。

\(m=1\) 应该相当好做，就是选 \(K\) 段不相交的段，使收益最大。容易想到线段树优化模拟费用流，复杂度 \(O(K\log n)\)。（因为太麻烦了所以写的 dp）

\(m=2\) 的话，同样写 dp，就考虑当前只选第一列、只选第二列或两列一起选三种情况。关键在于如何设计状态。如果用 \(dp[i][0/1/2]\) 来表示当前处理到第 \(i\) 行，转移状态 0~2 的话，转移的时候可能会出现如下的尴尬情形。

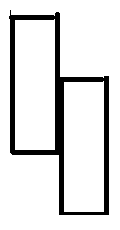
这两列有相交的部分，但是它们却属于不同的段。按照上述的状态，是没法转移的，因为当 \(dp[i][0]\) 用 \(dp[j][1]\) 转移，可能覆盖了之前 \(dp[j][1]\) 转移时的 \(dp[l][0]\) 的部分。

这和之前 yl 学长出的一道题很像。大概是有 \(n\) 个任务，每个任务可以由不同的两个人来完成，花费的时间不一样。且如果当前任务完成了或正在完成中才能去完成下一个任务。两个人可以同时在做任务，和这道题的转移很像。类比这道题，用 \(dp[i][j][k]\) 表示第 1 列正在位置 \(i\) ，第二列正在位置 \(j\) ，已经选了 \(k\) 个矩形的最大收益。那么上述转移就可以实现了。

1. 可以直接继承上一轮的状态

\[\max\{dp[i-1][j][k],dp[i][j-1][k]\} \]

2. 选择单独的一列为一个矩形 (其中 \(S\) 是前缀和)。

\[\max\{\max\limits_{0\leq l<i}\{dp[l][j][k-1]+S_{i,1}-S_{l,1}\},\max\limits_{0\leq l<j}\{dp[i][l][k-1]+S_{j,2}-S_{l,2}\}\} \]

3. 或者当 \(i=j\) 时，可以形成一个大矩形。

\[\max\limits_{0\leq l<i}\{dp[l][l][k-1]+(S_{i,1}+S_{i,2})-(S_{l,1}+S_{l,2})\} \]

#include<stdio.h>
#include<string.h>
#define N 107

namespace Case1{
    int a[N][3];
    int dp[N][N][11];
}

namespace Case2{
    int dp[N][11],a[N];
}

int n,m,K;
inline int max(int x,int y){return x>y? x:y;}
int main(){
    scanf("%d%d%d",&n,&m,&K);
    if(m==1){
        using namespace Case2;
        memset(dp,-63,sizeof(dp));
        dp[0][0]=0;
        for(int i=1;i<=n;i++) scanf("%d",&a[i]),a[i]+=a[i-1],dp[i][0]=0;
        for(int i=1;i<=n;i++)
            for(int k=1;k<=K;k++){
                dp[i][k]=dp[i-1][k];
                for(int j=0;j<i;j++)
                    dp[i][k]=max(dp[i][k],dp[j][k-1]+a[i]-a[j]);
            }
        printf("%d",dp[n][K]);    
    }else{
        using namespace Case1;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                scanf("%d",&a[i][j]),a[i][j]+=a[i-1][j];
        memset(dp,-63,sizeof(dp));
        for(int i=0;i<=K;i++) dp[0][0][i]=0;
        for(int i=0;i<=n;i++)
            for(int j=0;j<=n;j++) dp[i][j][0]=0;
        for(int i=0;i<=n;i++)
            for(int j=0;j<=n;j++)
                for(int k=1;k<=K;k++){
                    if(i) dp[i][j][k]=max(dp[i][j][k],dp[i-1][j][k]);
                    if(j) dp[i][j][k]=max(dp[i][j][k],dp[i][j-1][k]);
                    for(int l=0;l<i;l++)
                        dp[i][j][k]=max(dp[i][j][k],dp[l][j][k-1]+a[i][1]-a[l][1]);
                    for(int l=0;l<j;l++)
                        dp[i][j][k]=max(dp[i][j][k],dp[i][l][k-1]+a[j][2]-a[l][2]);
                    if(i==j) for(int l=0;l<i;l++)
                        dp[i][j][k]=max(dp[i][j][k],dp[l][l][k-1]+a[i][1]-a[l][1]+a[j][2]-a[l][2]);
                }
        printf("%d",dp[n][n][K]);
    }
}