[2020多校联考]四个质数的和

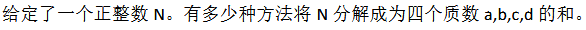
Solution

有一个显然的方法是筛出所有素数，再枚举其中三个，判断一下剩下的是不是素数，但十万以内的素数有九千多个，考虑优化。利用折半的思想，先将所有两个素数能并出来方案预处理出来，用 \(mp[x]\) 表示 \(x\) 用两个素数能凑出来的方案数。然后再枚举后面两个素数 ，记为 \(p_1\) 和 \(p_2\)，如果 \(p_1\) 和 \(p_2\) 相同，就将答案累加上 \(mp[n-p_i-p_j]\)；否则还要乘一个 \(2\)。再加一点小剪枝，差不多就能过。

#include<stdio.h>
#define N 100007

bool mark[N];
int n,p[N],cnt=0,T,mp[N];
int main(){
    freopen("plus.in","r",stdin);
    freopen("plus.out","w",stdout);
    scanf("%d",&T);
    mark[1]=1;
    for(int i=2;i<N;i++){
        if(!mark[i]) p[++cnt]=i;
        for(int j=1;j<=cnt&&p[j]*i<N;j++){
            mark[p[j]*i]=1;
            if(i%p[j]==0) break;
        }
    }
    for(int i=1;i<=cnt;i++)
        for(int j=1;j<=cnt;j++){
            if(p[i]+p[j]>=N) break;
            mp[p[i]+p[j]]++;
        }
    while(T--){
        scanf("%d",&n);
        long long ans=0;
        for(int i=1;i<=cnt;i++){
            if(p[i]>=n) break;
            for(int j=i;j<=cnt;j++){
                if(p[i]+p[j]>=n) break;
                ans+=1LL*(p[i]!=p[j]? 2:1)*mp[n-p[i]-p[j]];
            }
        }
        printf("%lld\n",ans);
    }
}

Tips

实际上，后面不需要再枚举两个 \(p\) ，考场上蠢了，居然还能过……答案直接为 \(\sum_{i=1}^{n} mp_i\times mp_{n-i}\)

#include<stdio.h>
#define N 100007

bool mark[N];
int n,p[N],cnt=0,T,mp[N];
int main(){
    freopen("plus.in","r",stdin);
    freopen("plus.out","w",stdout);
    scanf("%d",&T);
    mark[1]=1;
    for(int i=2;i<N;i++){
        if(!mark[i]) p[++cnt]=i;
        for(int j=1;j<=cnt&&p[j]*i<N;j++){
            mark[p[j]*i]=1;
            if(i%p[j]==0) break;
        }
    }
    for(int i=1;i<=cnt;i++)
        for(int j=1;j<=cnt;j++){
            if(p[i]+p[j]>=N) break;
            mp[p[i]+p[j]]++;
        }
    while(T--){
        scanf("%d",&n);
        long long ans=0;
        for(int i=1;i<=n;i++) ans+=1LL*mp[i]*mp[n-i];
        printf("%lld\n",ans);
    }
}