斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用。
1、递归
public static long f1(int n) { if (n < 1) { throw new Exception("输入参数小于1"); } if (n == 1 || n == 2) { return 1; } else { return f1(n - 1) + f1(n - 2); } }
递归比较直观,但是由于是逆推,重复计算,所以效率低下,可加入map对象查找进行优化,但是由于递归的本质,会导致栈溢出风险,不推荐。
2、顺序加
public static long f2(int n) { if (n <= 0) { throw new Exception("输入参数小于1"); } if (n == 1 || n == 2) { return 1; } long a = 1; long b = 1; long c = 0; for (int i = 3; i <= n; i++) { c = a + b; a = b; b = c; } return c; }
无递归栈溢出风险,效率高,时间复杂度O(n).3、数学表达式计算
通过数学推导,可得出如下结论:
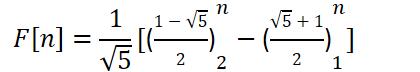
public static long f3(int n) { double result = 0; double temp = Math.Sqrt(5.0); result = (Math.Pow((1 + temp) / 2, n) - Math.Pow((1 - temp) / 2, n)) / temp; return (long)result; }
时间复杂度依赖于系统计算方式。但是由于计算机精度问题,导致该方式在n=71之后就不再准确。
4、矩阵快速幂
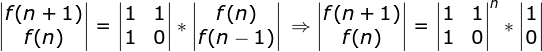
public static long f4(int n) { if (n <= 0) { throw new Exception("输入参数小于1"); } if (n == 1 || n == 2) { return 1; } //单位矩阵 long[][] result = { new long[] {1}, new long[] {0}}; long[][] tem = { new long[] { 1,1 }, new long[] { 1, 0 } }; while (n != 0) { if ((n & 1) == 1) { result = matrixMultiply(tem, result); } tem = matrixMultiply(tem, tem); //右移一位并赋值 n >>= 1; } return result[1][0]; } private static long[][] matrixMultiply(long[][] a, long[][] b) { int rows = a.Length; int cols = b[0].Length; long[][] matrix = new long[rows][]; for (int i = 0; i < matrix.Length; i++) { matrix[i] = new long[cols]; } for (int i = 0; i < a.Length; i++) { for (int j = 0; j < b[0].Length; j++) { for (int k = 0; k < a[i].Length; k++) { matrix[i][j] += a[i][k] * b[k][j]; } } } return matrix; }
虽然matrixMultiply方法中为for循环嵌套,但是由于斐波那契数列为2*2矩阵,其循环次数一定,时间复杂度可看为O(1),故矩阵快速幂方式求解斐波那契数列时间复杂度为O(logn)。
做下测试:
static void Main(string[] args) { var ddd=f1(40); //递归是最慢的 var ddd2 = f2(40); var ddd3 = f3(40); var ddd4 = f4(40); Console.WriteLine(ddd); Console.WriteLine(ddd2); Console.WriteLine(ddd3); Console.WriteLine(ddd4); Console.ReadKey(); }
下面为矩阵乘法备注:
大多数人在高中,或者大学低年级,都上过一门课《线性代数》。这门课其实是教矩阵。
刚学的时候,还蛮简单的,矩阵加法就是相同位置的数字加一下。
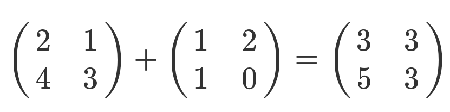
矩阵减法也类似。
矩阵乘以一个常数,就是所有位置都乘以这个数。
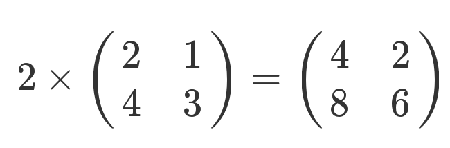
但是,等到矩阵乘以矩阵的时候,一切就不一样了。
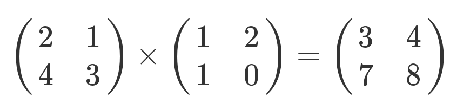
这个结果是怎么算出来的?
教科书告诉你,计算规则是,第一个矩阵第一行的每个数字(2和1),各自乘以第二个矩阵第一列对应位置的数字(1和1),然后将乘积相加( 2 x 1 + 1 x 1),得到结果矩阵左上角的那个值3。
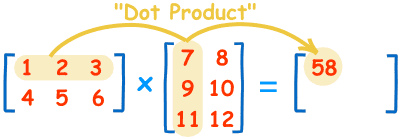
也就是说,结果矩阵第m行与第n列交叉位置的那个值,等于第一个矩阵第m行与第二个矩阵第n列,对应位置的每个值的乘积之和。
怎么会有这么奇怪的规则?
我一直没理解这个规则的含义,导致《线性代数》这门课就没学懂。研究生时发现,线性代数是向量计算的基础,很多重要的数学模型都要用到向量计算,所以我做不了复杂模型。这一直让我有点伤心。
前些日子,受到一篇文章的启发,我终于想通了,矩阵乘法到底是什么东西。关键就是一句话,矩阵的本质就是线性方程式,两者是一一对应关系。如果从线性方程式的角度,理解矩阵乘法就毫无难度。
下面是一组线性方程式。
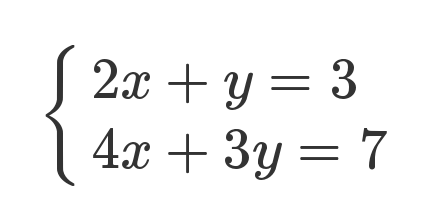
矩阵的最初目的,只是为线性方程组提供一个简写形式。
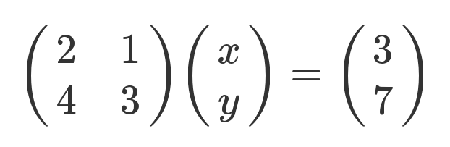
老实说,从上面这种写法,已经能看出矩阵乘法的规则了:系数矩阵第一行的2和1,各自与 x 和 y 的乘积之和,等于3。不过,这不算严格的证明,只是线性方程式转为矩阵的书写规则。
下面才是严格的证明。有三组未知数 x、y 和 t,其中 x 和 y 的关系如下。
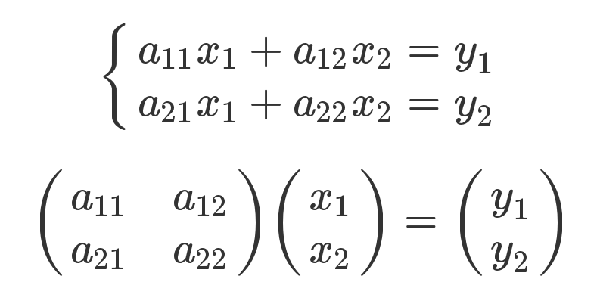
x 和 t 的关系如下。
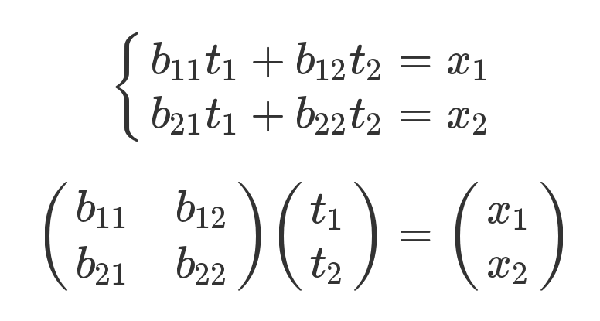
有了这两组方程式,就可以求 y 和 t 的关系。从矩阵来看,很显然,只要把第二个矩阵代入第一个矩阵即可。
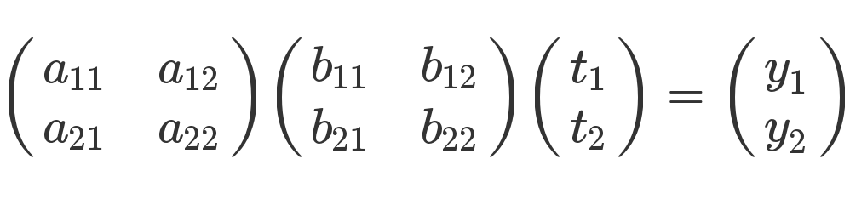
从方程式来看,也可以把第二个方程组代入第一个方程组。
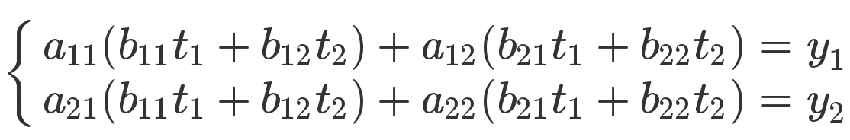
上面的方程组可以整理成下面的形式。
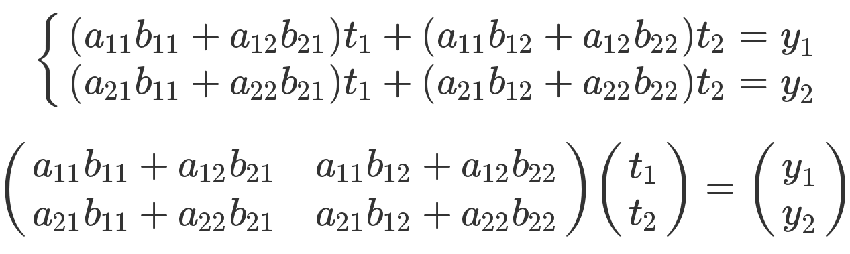
最后那个矩阵等式,与前面的矩阵等式一对照,就会得到下面的关系。
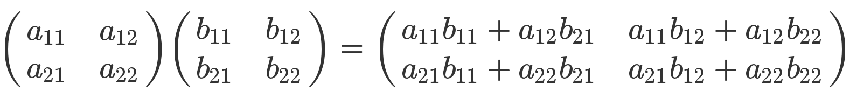
矩阵乘法的计算规则,从而得到证明。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律