Leetcode——树和图(1)
二叉树的层序遍历
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
示例:
二叉树:[3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[3],
[9,20],
[15,7]
]
广度优先搜索 BFS
建立一个 queue,然后先把根节点放进去,这时候找根节点的左右两个子节点,这时候去掉根节点,此时 queue 里的元素就是下一层的所有节点,
用一个 for 循环遍历它们,然后存到一个一维向量里,遍历完之后再把这个一维向量存到二维向量里,以此类推,可以完成层序遍历
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if (!root) return {};
vector<vector<int>> res;
queue<TreeNode*> q{{root}};
while (!q.empty()) {
vector<int> oneLevel;
for (int i = q.size(); i > 0; --i) {
TreeNode *t = q.front(); q.pop();
oneLevel.push_back(t->val);
if (t->left) q.push(t->left);
if (t->right) q.push(t->right);
}
res.push_back(oneLevel);
}
return res;
}
};
递归
建立一个 queue,然后先把根节点放进去,这时候找根节点的左右两个子节点,这时候去掉根节点,此时 queue 里的元素就是下一层的所有节点,
用一个 for 循环遍历它们,然后存到一个一维向量里,遍历完之后再把这个一维向量存到二维向量里,以此类推,可以完成层序遍历
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
levelorder(root, 0, res);
return res;
}
void levelorder(TreeNode* node, int level, vector<vector<int>>& res) {
if (!node) return;
if (res.size() == level) res.push_back({});
res[level].push_back(node->val);
if (node->left) levelorder(node->left, level + 1, res);
if (node->right) levelorder(node->right, level + 1, res);
}
};
二叉树的层次遍历 II
给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其自底向上的层次遍历为:
[
[15,7],
[9,20],
[3]
]
广度优先搜索 BFS
class Solution {
public:
vector<vector<int> > levelOrderBottom(TreeNode* root) {
if (!root) return {};
vector<vector<int>> res;
queue<TreeNode*> q{{root}};
while (!q.empty()) {
vector<int> oneLevel;
for (int i = q.size(); i > 0; --i) {
TreeNode *t = q.front(); q.pop();
oneLevel.push_back(t->val);
if (t->left) q.push(t->left);
if (t->right) q.push(t->right);
}
res.insert(res.begin(), oneLevel);
}
return res;
}
};
递归
使用一个变量level来标记当前的深度,初始化带入0,表示根结点所在的深度。
由于需要返回的是一个二维数组res,开始时我们又不知道二叉树的深度,不知道有多少层,所以无法实现申请好二维数组的大小,只有在遍历的过程中不断的增加。
那么我们什么时候该申请新的一层了呢,当level等于二维数组的大小的时候,为啥是等于呢,不是说要超过当前的深度么,这是因为level是从0开始的,就好比一个长度为n的数组A,你访问A[n]是会出错的,当level等于数组的长度时,就已经需要新申请一层了,我们新建一个空层,继续往里面加数字
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> res;
levelorder(root, 0, res);
return vector<vector<int>> (res.rbegin(), res.rend());
}
void levelorder(TreeNode* node, int level, vector<vector<int>>& res) {
if (!node) return;
if (res.size() == level) res.push_back({});
res[level].push_back(node->val);
if (node->left) levelorder(node->left, level + 1, res);
if (node->right) levelorder(node->right, level + 1, res);
}
};
二叉树的中序遍历
给定一个二叉树,返回它的中序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [1,3,2]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
递归
对左子结点调用递归函数,根节点访问值,右子节点再调用递归函数
class Solution {
public:
vector<int> inorderTraversal(TreeNode *root) {
vector<int> res;
inorder(root, res);
return res;
}
void inorder(TreeNode *root, vector<int> &res) {
if (!root) return;
if (root->left) inorder(root->left, res);
res.push_back(root->val);
if (root->right) inorder(root->right, res);
}
};
栈
从根节点开始,先将根节点压入栈,然后再将其所有左子结点压入栈,然后取出栈顶节点,保存节点值,
再将当前指针移到其右子节点上,若存在右子节点,则在下次循环时又可将其所有左子结点压入栈中。
这样就保证了访问顺序为左-根-右
class Solution {
public:
vector<int> inorderTraversal(TreeNode *root) {
vector<int> res;
stack<TreeNode*> s;
TreeNode *p = root;
while (p || !s.empty()) {
while (p) {
s.push(p);
p = p->left;
}
p = s.top(); s.pop();
res.push_back(p->val);
p = p->right;
}
return res;
}
};
把结点值加入结果 res 的步骤从 if 中移动到了 else 中,因为中序遍历的顺序是左-根-右
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> s;
TreeNode *p = root;
while (!s.empty() || p) {
if (p) {
s.push(p);
p = p->left;
} else {
p = s.top(); s.pop();
res.push_back(p->val);
p = p->right;
}
}
return res;
}
};
二叉树的前序遍历
给定一个二叉树,返回它的 前序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [1,2,3]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
栈
先序遍历的顺序是"根-左-右", 算法为:
-
把根节点 push 到栈中
-
循环检测栈是否为空,若不空,则取出栈顶元素,保存其值,然后看其右子节点是否存在,若存在则 push 到栈中。再看其左子节点,若存在,则 push 到栈中。
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
if (!root) return {};
vector<int> res;
stack<TreeNode*> s{{root}};
while (!s.empty()) {
TreeNode *t = s.top(); s.pop();
res.push_back(t->val);
if (t->right) s.push(t->right);
if (t->left) s.push(t->left);
}
return res;
}
};
辅助结点p初始化为根结点,while 循环的条件是栈不为空或者辅助结点p不为空,
在循环中首先判断如果辅助结点p存在,那么先将p加入栈中,然后将p的结点值加入结果 res 中,此时p指向其左子结点。
否则如果p不存在的话,表明没有左子结点,取出栈顶结点,将p指向栈顶结点的右子结点
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> st;
TreeNode *p = root;
while (!st.empty() || p) {
if (p) {
st.push(p);
res.push_back(p->val);
p = p->left;
} else {
p = st.top(); st.pop();
p = p->right;
}
}
return res;
}
};
二叉树的后序遍历
给定一个二叉树,返回它的 后序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [3,2,1]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
后序的顺序是左-右-根,所以当一个结点值被取出来时,它的左右子结点要么不存在,要么已经被访问过了。
先将根结点压入栈,然后定义一个辅助结点 head,while 循环的条件是栈不为空,
在循环中,首先将栈顶结点t取出来,如果栈顶结点没有左右子结点,或者其左子结点是 head,或者其右子结点是 head 的情况下。
将栈顶结点值加入结果 res 中,并将栈顶元素移出栈,然后将 head 指向栈顶元素;
否则的话就看如果右子结点不为空,将其加入栈,再看左子结点不为空的话,就加入栈,
注意这里先右后左的顺序是因为栈的后入先出的特点,可以使得左子结点先被处理。
下面来看为什么是这三个条件呢,
首先如果栈顶元素如果没有左右子结点的话,说明其是叶结点,
而且入栈顺序保证了左子结点先被处理,所以此时的结点值就可以直接加入结果 res 了,
然后移出栈,将 head 指向这个叶结点,这样的话 head 每次就是指向前一个处理过并且加入结果 res 的结点,那么如果栈顶结点的左子结点或者右子结点是 head 的话,说明其子结点已经加入结果 res 了,那么就可以处理当前结点了。
head 是指向上一个被遍历完成的结点,由于后序遍历的顺序是左-右-根,所以一定会一直将结点压入栈,一直到把最左子结点(或是最左子结点的最右子结点)压入栈后,开始进行处理。
一旦开始处理了,head 就会被重新赋值。所以 head 初始化值并没有太大的影响,
唯一要注意的是不能初始化为空,因为在判断是否打印出当前结点时除了判断是否是叶结点,还要看 head 是否指向其左右子结点,
如果 head 指向左子结点,那么右子结点一定为空,因为入栈顺序是根-右-左,不存在右子结点还没处理,就直接去处理根结点了的情况。若 head 指向右子结点,则是正常的左-右-根的处理顺序。那么回过头来在看,
若 head 初始化为空,且此时正好左子结点不存在,那么在压入根结点时,head 和左子结点相等就成立了,此时就直接打印根结点了,明显是错的。
所以 head 只要不初始化为空,一切都好说,甚至可以新建一个结点也没问题。将 head 初始化为 root,也可以,就算只有一个 root 结点,那么在判定叶结点时就将 root 打印了,然后就跳出 while 循环了,也不会出错
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
if (!root) return {};
vector<int> res;
stack<TreeNode*> s{{root}};
TreeNode *head = root;
while (!s.empty()) {
TreeNode *t = s.top();
if ((!t->left && !t->right) || t->left == head || t->right == head) {
res.push_back(t->val);
s.pop();
head = t;
} else {
if (t->right) s.push(t->right);
if (t->left) s.push(t->left);
}
}
return res;
}
};
先将先序遍历的根-左-右顺序变为根-右-左,再翻转变为后序遍历的左-右-根,翻转还是改变结果 res 的加入顺序,然后把更新辅助结点p的左右顺序换一下即可
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> s;
TreeNode *p = root;
while (!s.empty() || p) {
if (p) {
s.push(p);
res.insert(res.begin(), p->val);
p = p->right;
} else {
TreeNode *t = s.top(); s.pop();
p = t->left;
}
}
return res;
}
};
二叉树的锯齿形层次遍历
给定一个二叉树,返回其节点值的锯齿形层次遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回锯齿形层次遍历如下:
[
[3],
[20,9],
[15,7]
]
方法一
利用层序遍历,并使用一个变量 cnt 来统计当前的层数(从0开始),将所有的奇数层的结点值进行翻转一下即可
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
if (!root) return {};
vector<vector<int>> res;
queue<TreeNode*> q{{root}};
int cnt = 0;
while (!q.empty()) {
vector<int> oneLevel;
for (int i = q.size(); i > 0; --i) {
TreeNode *t = q.front(); q.pop();
oneLevel.push_back(t->val);
if (t->left) q.push(t->left);
if (t->right) q.push(t->right);
}
if (cnt % 2 == 1) reverse(oneLevel.begin(), oneLevel.end());
res.push_back(oneLevel);
++cnt;
}
return res;
}
};
方法二
由于每层的结点数是知道的,就是队列的元素个数,所以可以直接初始化数组的大小。
此时使用一个变量 leftToRight 来标记顺序,初始时是 true,
当此变量为 true 的时候,每次加入数组的位置就是i本身,
若变量为 false 了,则加入到 size-1-i 位置上,这样就直接相当于翻转了数组。
每层遍历完了之后,需要翻转 leftToRight 变量,同时不要忘了将 oneLevel 加入结果 res
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
if (!root) return {};
vector<vector<int>> res;
queue<TreeNode*> q{{root}};
bool leftToRight = true;
while (!q.empty()) {
int size = q.size();
vector<int> oneLevel(size);
for (int i = 0; i < size; ++i) {
TreeNode *t = q.front(); q.pop();
int idx = leftToRight ? i : (size - 1 - i);
oneLevel[idx] = t->val;
if (t->left) q.push(t->left);
if (t->right) q.push(t->right);
}
leftToRight = !leftToRight;
res.push_back(oneLevel);
}
return res;
}
};
递归
实际上用的是先序遍历,递归函数需要一个变量 level 来记录当前的深度,由于 level 是从0开始的,
假如结果 res 的大小等于 level,就需要在结果 res 中新加一个空集,这样可以保证 res[level] 不会越界。
取出 res[level] 之后,判断 levle 的奇偶,
若其为偶数,则将 node->val 加入 oneLevel 的末尾,
若为奇数,则加在 oneLevel 的开头。然后分别对 node 的左右子结点调用递归函数,此时要传入 level+1 即可
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> res;
helper(root, 0, res);
return res;
}
void helper(TreeNode* node, int level, vector<vector<int>>& res) {
if (!node) return;
if (res.size() <= level) {
res.push_back({});
}
vector<int> &oneLevel = res[level];
if (level % 2 == 0) oneLevel.push_back(node->val);
else oneLevel.insert(oneLevel.begin(), node->val);
helper(node->left, level + 1, res);
helper(node->right, level + 1, res);
}
};
二叉搜索树迭代器
实现一个二叉搜索树迭代器。你将使用二叉搜索树的根节点初始化迭代器。
调用 next() 将返回二叉搜索树中的下一个最小的数。
示例:
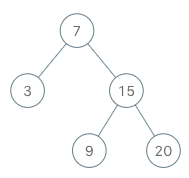
BSTIterator iterator = new BSTIterator(root);
iterator.next(); // 返回 3
iterator.next(); // 返回 7
iterator.hasNext(); // 返回 true
iterator.next(); // 返回 9
iterator.hasNext(); // 返回 true
iterator.next(); // 返回 15
iterator.hasNext(); // 返回 true
iterator.next(); // 返回 20
iterator.hasNext(); // 返回 false
提示:
next()和hasNext()操作的时间复杂度是 O(1),并使用 O(h) 内存,其中 h 是树的高度。- 你可以假设
next()调用总是有效的,也就是说,当调用next()时,BST 中至少存在一个下一个最小的数。
二叉树的中序遍历的非递归形式,需要额外定义一个栈来辅助,二叉搜索树的建树规则就是左<根<右,用中序遍历即可从小到大取出所有节点
class BSTIterator {
public:
BSTIterator(TreeNode *root) {
while (root) {
s.push(root);
root = root->left;
}
}
bool hasNext() {
return !s.empty();
}
int next() {
TreeNode *n = s.top();
s.pop();
int res = n->val;
if (n->right) {
n = n->right;
while (n) {
s.push(n);
n = n->left;
}
}
return res;
}
private:
stack<TreeNode*> s;
};
二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
深度优先搜索
C++
class Solution {
public:
int maxDepth(TreeNode* root) {
if (!root) return 0;
return 1 + max(maxDepth(root->left), maxDepth(root->right));
}
};
Java
public class Solution {
public int maxDepth(TreeNode root) {
return root == null ? 0 : (1 + Math.max(maxDepth(root.left), maxDepth(root.right)));
}
}
队列
使用层序遍历二叉树,然后计数总层数,即为二叉树的最大深度,
注意 while 循环中的 for 循环的写法有个 trick,一定要将 q.size() 放在初始化里,而不能放在判断停止的条件中,因为q的大小是随时变化的,所以放停止条件中会出错
C++
class Solution {
public:
int maxDepth(TreeNode* root) {
if (!root) return 0;
int res = 0;
queue<TreeNode*> q{{root}};
while (!q.empty()) {
++res;
for (int i = q.size(); i > 0; --i) {
TreeNode *t = q.front(); q.pop();
if (t->left) q.push(t->left);
if (t->right) q.push(t->right);
}
}
return res;
}
};
Java
public class Solution {
public int maxDepth(TreeNode root) {
if (root == null) return 0;
int res = 0;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
++res;
for (int i = q.size(); i > 0; --i) {
TreeNode t = q.poll();
if (t.left != null) q.offer(t.left);
if (t.right != null) q.offer(t.right);
}
}
return res;
}
}
平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
1
/ \
2 2
/ \
3 3
/ \
4 4
返回 false 。
方法一
平衡二叉树是每一个结点的两个子树的深度差不能超过1,
需要一个求各个点深度的函数,然后对每个节点的两个子树来比较深度差,时间复杂度为O(NlgN)
class Solution {
public:
bool isBalanced(TreeNode *root) {
if (!root) return true;
if (abs(getDepth(root->left) - getDepth(root->right)) > 1) return false;
return isBalanced(root->left) && isBalanced(root->right);
}
int getDepth(TreeNode *root) {
if (!root) return 0;
return 1 + max(getDepth(root->left), getDepth(root->right));
}
};
方法二
对于每一个节点,我们通过checkDepth方法递归获得左右子树的深度,
如果子树是平衡的,则返回真实的深度,若不平衡,直接返回-1,此方法时间复杂度O(N),空间复杂度O(H)
class Solution {
public:
bool isBalanced(TreeNode *root) {
if (checkDepth(root) == -1) return false;
else return true;
}
int checkDepth(TreeNode *root) {
if (!root) return 0;
int left = checkDepth(root->left);
if (left == -1) return -1;
int right = checkDepth(root->right);
if (right == -1) return -1;
int diff = abs(left - right);
if (diff > 1) return -1;
else return 1 + max(left, right);
}
};



