【蓝桥杯/算法训练】Sticks 剪枝算法 (附胜利大逃亡）
剪枝算法
大概理解是通过分析问题，发现一些判断条件，避免不必要的搜索。通常应用在DFS 和 BFS 搜索算法中；剪枝策略就是寻找过滤条件，提前减少不必要的搜索路径。
Sticks
问题描述
George took sticks of the same length and cut them randomly until all parts became at most 50 units long. Now he wants to return sticks to the original state, but he forgot how many sticks he had originally and how long they were originally. Please help him and design a program which computes the smallest possible original length of those sticks. All lengths expressed in units are integers greater than zero.
输入格式
The input contains blocks of 2 lines. The first line contains the number of sticks parts after cutting, there are at most 64 sticks. The second line contains the lengths of those parts separated by the space. The last line of the file contains zero.
输出格式
The output should contains the smallest possible length of original sticks, one per line.
样例输入
9
5 2 1 5 2 1 5 2 1
4
1 2 3 4
0
样例输出
6
5
问题分析
题目意思：
乔治开始拿了a个长度均为L的木棍，随机锯木棍，最终把这a个木棍锯成了n个小块。根据n个小块及其各自长度，求出L可能的最小值。
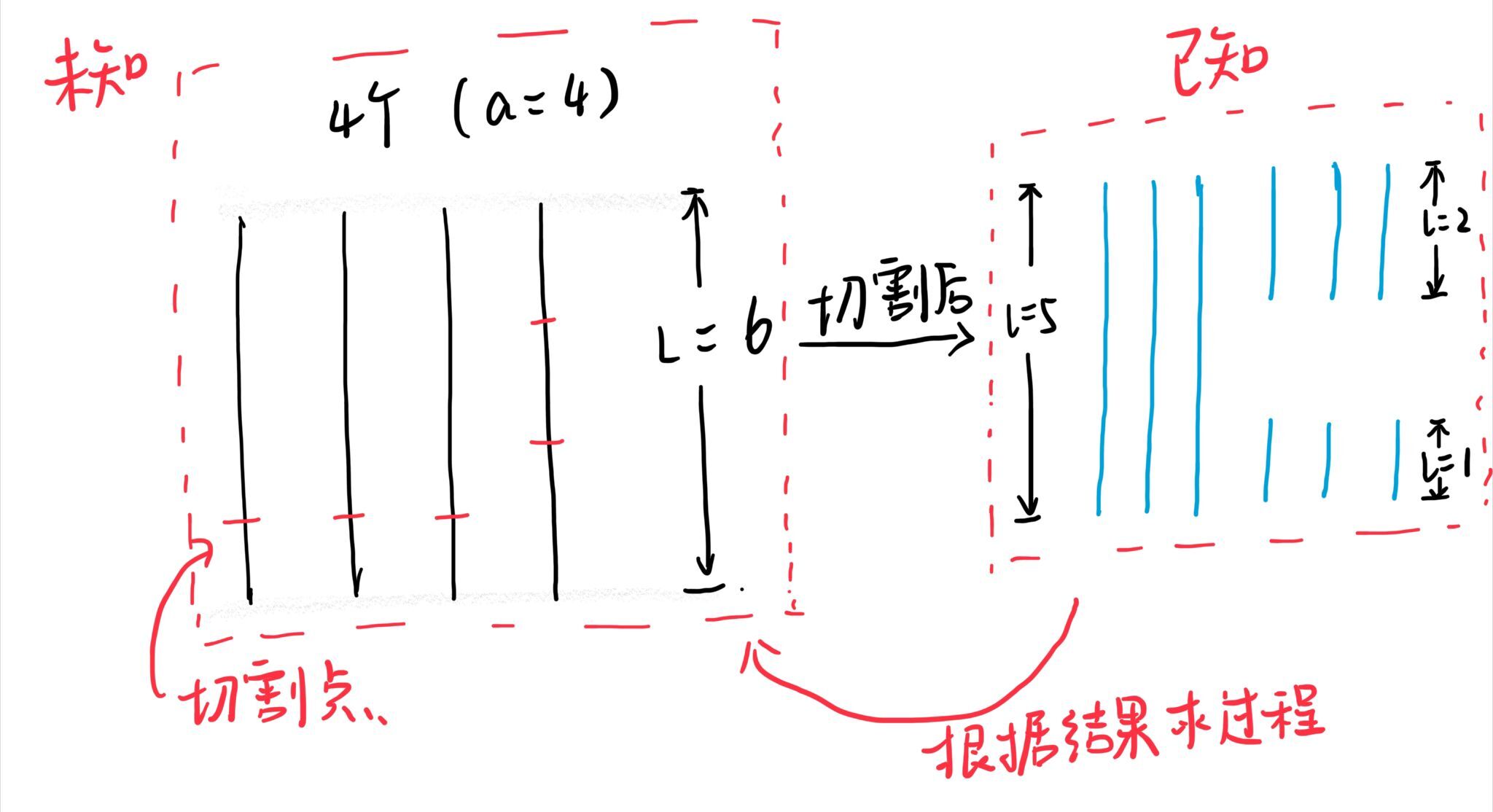
如上图，根据右边的结果求出左边的L最小值为6（为什么要求最小值？因为L还可能为12，48）
剪枝条件分析：
1.a为整数，故初始长度L一定是总长度sum的因数。
2.n个小木块中，长度长的木块凑成L长的搭配可能性更小，所以将这n个木块从大到小排序，从大的开始搜索
3.搜索过程总按照排序，前一个小木棍没有成功时这一个也一定不能成功，直接略过
4.当一个木块拼凑失败时，直接回溯，不再按照这个条件搜索
#include<bits/stdc++.h>
using namespace std;
#define MAX 65536
int a[MAX];
int vis[MAX];//是否已匹配的标志
int maxed;
int len; //木棍的数量
bool cmp(int x,int y)
{
return x>y;
}
//通过dfs判断是否可以拼凑成长度为k的木块
bool dfs(int sum,int cur,int res,int k) //k为假设的单个木块长度 ，res为已拼成木棍的数量 ,sum为当前正在拼凑的这一根木棍已有长度
{
if(res==maxed) //已成功拼完返回成功
{
return true;
}
for(int i=cur;i<len;i++) //len为切割后的木棍数量，一个个遍历 ，cur为目前搜索位置，cur前的为不符合条件的
{
//如果第i个木棍已计入，或者与前一个木棍等长且同样未计入（未计入表示方案不可行，所以这一个不用搜了，也不行）
if(vis[i]||(i&&a[i]==a[i-1]&&!vis[i-1]))
{
continue;
}
if(a[i]+sum==k) //成功拼成一个假定长度的小木块
{
vis[i] =1;
if(dfs(0,0,res+1,k)) //res+1即成功拼凑数量加一，开始拼下一个，sum，cur初始化为0
return true;
vis[i]=0; //表示虽然这一步拼成了长度为k的木块，但后面剩下的木块不能成功拼凑，故失败回溯
return false;
}
if(a[i]+sum<k) //没拼好
{
vis[i]=1;
if(dfs(a[i]+sum,i+1,res,k)) //递归继续循环将之拼为假设长度
return true;
vis[i]=0;
if(!sum)
return false; //最后仍不能拼成
}
}
return false;
}
int main()
{
int sum; //木棍总长度
while(cin>>len&&len)
{
sum=0;
for(int i=0;i<len;i++)
{
cin>>a[i];
sum+=a[i];
}
sort(a,a+len,cmp); //将木棍长度从大到小排序
int flag=0;
for(int i=a[0];i<=sum/2;i++)
{
if(sum%i==0) //可能的木棍的单独长度为sum的因子（因为初始为等长的完整的木棍
{
memset(vis,0,sizeof(vis)); //标记是否已用
maxed=sum/i; //可能的最多木棍数
if(dfs(0,0,0,i))
{
cout<<i<<endl;
flag=1;
break;
}
}
}
if(!flag)
{
cout<<sum<<endl;
}
}
return 0;
}
例子运行过程
eg：
输入：
9
5 2 1 5 2 1 5 2 1
输出：
6
代码转载自该博客
胜利大逃亡
题目描述：
Ignatius被魔王抓走了,有一天魔王出差去了,这可是Ignatius逃亡的好机会.魔王住在一个城堡里,城堡是一个ABC的立方体,可以被表示成A个B*C的矩阵,刚开始Ignatius被关在(0,0,0)的位置,离开城堡的门在(A-1,B-1,C-1)的位置,现在知道魔王将在T分钟后回到城堡,Ignatius每分钟能从一个坐标走到相邻的六个坐标中的其中一个.现在给你城堡的地图,请你计算出Ignatius能否在魔王回来前离开城堡(只要走到出口就算离开城堡,如果走到出口的时候魔王刚好回来也算逃亡成功),如果可以请输出需要多少分钟才能离开,如果不能则输出-1.
输入：
输入数据的第一行是一个正整数K,表明测试数据的数量.每组测试数据的第一行是四个正整数A,B,C和T(1<=A,B,C<=50,1<=T<=1000),它们分别代表城堡的大小和魔王回来的时间.然后是A块输入数据(先是第0块,然后是第1块,第2块......),每块输入数据有B行,每行有C个正整数,代表迷宫的布局,其中0代表路,1代表墙。
输出：
对于每组测试数据,如果Ignatius能够在魔王回来前离开城堡,那么请输出他最少需要多少分钟,否则输出-1.
样例输入：
1
3 3 4 20
0 1 1 1
0 0 1 1
0 1 1 1
1 1 1 1
1 0 0 1
0 1 1 1
0 0 0 0
0 1 1 0
0 1 1 0
样例输出：
11
分析问题可知，该题即寻找出逃路径，可以看作查找。
查找空间：从点(0,0,0)到点（A-1,B-1,C-1)的合法路径
查找目标：在查找空间中的所有路径中寻找一条最短的路径，即步数最少的路径
查找方法：可以看作回溯，走不通了就回退。
可以定义一个时刻的状态，（x,y,z,t)即由起点到（x,y,z)经历的最短时间t;各个状态按照其被查找的顺序依次转移扩展，使用队列。
该例子使用广度优先搜索的办法，但是如果全部搜完，则复杂度太大，如果仅需十步则搜索过程也达到了6^10。所以需要剪枝，寻找减少搜索的条件；
分析题目可知，剪枝条件：
- 当遇到墙时不能走，则通过墙这一点的后面也均不用搜索；
- 当搜索时走到立方体外则不用搜索；
- 若该坐标已经被标记搜索过了，则不用再次搜索，因为每走一步时间会增加，所以后来经过该点的路线所费时间一定比第一次经过标记时的时间长，所以后来的均不用搜索；
结合广度优先搜索的实现方法：队列，可以在遍历中丢弃很多“枝”,故方法可行；
我看问题时的几个疑惑：
- 如何保证已经搜索的路线（即按照上述剪枝后）是最短路线？
这个应该是由剪枝条件三保证的，因为每个点被标记是否搜索过时是第一次经过此点，是从起点到此点的最短距离。如果绕路后过来则直接舍弃了（时间比第一次来长）； - 计时和路线如何匹配，因为是立方体总觉得用…三维数组？可能是我思维太不灵活了…
点的多属性（三维坐标、从起点到该点的时间）用结构体表示。 - 最开始想着重复的点如果走完周围的六个点又走回去了怎么办？
也是因为我思维不灵活导致的……就是加个mark数组标记一下的问题
#include<bits/stdc++.h>
using namespace std;
#define MAX 51
#define MAXT 1001
struct N{
int x,y,z;
int t;
};
queue<N> q;
int maze[MAX][MAX][MAX];
bool mark[MAX][MAX][MAX];
int go[][3]={
1,0,0,
-1,0,0,
0,1,0,
0,-1,0,
0,0,1,
0,0,-1
};
int main()
{
freopen("data.txt","r",stdin);
int A,B,C,T;
cin>>A>>B>>C>>T;
for(int i=0;i<A;i++)
{
for(int j=0;j<B;j++)
{
for(int k=0;k<C;k++)
{
cin>>maze[i][j][k];
mark[i][j][k]=false;
}
}
}
N tn;
tn.x=0;
tn.y=0;
tn.z=0;
tn.t=0;
q.push(tn);
int flag=-1;
while(!q.empty())
{
N tmp=q.front();
q.pop();
for(int i=0;i<6;i++)
{
int tx=tmp.x+go[i][0];
int ty=tmp.y+go[i][1];
int tz=tmp.z+go[i][2];
int tt=tmp.t+1;
if(mark[tx][ty][tz]) continue;
if(maze[tx][ty][tz]) continue;
if(tx<0||ty<0||tz<0||tx>=A||ty>=B||tz>=C) continue;
if(tx==A-1&&ty==B-1&&tz==C-1)
{
if(tt<=T)
{
cout<<tt<<endl;
flag=1;
break;
}
}
N tmp2;
tmp2.x=tx;
tmp2.y=ty;
tmp2.z=tz;
tmp2.t=tt;
q.push(tmp2);
mark[tx][ty][tz]=true;
}
}
if(flag==-1)
{
cout<<flag<<endl;
}
return 0;
}
