《统计学习方法》笔记二 感知机

本系列笔记内容参考来源为李航《统计学习方法》

感知机（perceptron）是二分类的线性分类模型，输入为实例的特征向量，输出为实例的类别，取±1。感知机对应与输入空间中将实例划分为正负两类的分离超平面，属于判别模型。感知机学习旨在求出将训练数据进行线性划分的分离超平面，为此，导入基于误分类的损失函数，利用梯度下降法对损失函数进行极小化，求得感知机模型。感知机算法具有简单而易于实现的优点，分为原始形式和对偶形式，感知机预测是用学习得到的感知机模型对新的输入实例进行分类。

感知机模型

几何解释如下：

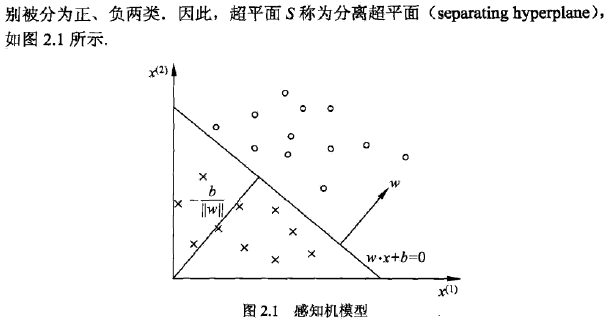
感知机学习策略

首先定义了数据集的线性可分性，简单说即对一个数据集，存在某一超平面可将数据集的正、负实例点完全划分到超平面的两侧。

确定学习策略即定义（经验）损失函数并将损失函数极小化。若选择误分类点的总数，这样的损失函数不是参数ω、b的连续可导函数，不易优化。因此选择误分类点到超平面S的总距离。平面上一点x0到超平面的距离为：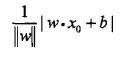

 

 对于误分类点有-y_i(ωx_i+b)>0，则误分类点到超平面的距离为

感知机学习算法

原始形式

对偶形式

Gram矩阵计算如下：

 

原始形式收敛性

采用不同的初值或选取不同的误分类点，得出的解可以不同。

此外，书中证明了原始形式算法收敛，并且经过有限次迭代可得到一个将训练数据集完全划分的分离超平面及感知机模型。

定理如下