吴恩达机器学习笔记
1 机器学习的含义
(1)Field of study that gives computers the ability to learn without being explicitly programmed 在没有显示编程的情况下,让计算机具有学习的能力
(2)A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E 对于一个程序,给它一个任务T和一个性能测量方法P,如果在经验E的影响下,P对T的测量结果得到了改进,那么就说该程序从E中学习
2 机器学习的分类

无监督学习:
- 无监督的学习使我们能够很少或根本不知道我们的结果应该是什么样子。
- 我们可以从数据中推导出结构,我们不一定知道变量的影响。
- 我们可以通过基于数据中变量之间的关系对数据进行聚类来推导出这种结构。
- 在无监督学习的基础上,没有基于预测结果的反馈。
例:
- 聚类:搜集一百万个不同的基因,并找到一种方法,将这些基因自动分组,这些基因组通过不同的变量(例如寿命,位置,角色等)相似或相关
- 非聚类:“鸡尾酒会算法”,可以让你在混乱的环境中找到结构。 (即在鸡尾酒会上从声音网格中识别个别的声音和音乐)
Lecture 4
多元线性回归:拥有多个变量的线性回归
notation:
- n:特征的数目
- x(i):训练集中的第i个输入
- xj(i):第i个训练项中第j个特征的值
3 线性回归模型

目标是minimize代价函数
4 特征缩放/均值归一化
我们可以通过让每个输入值大致相同的范围来加速梯度下降。这是因为它会在小范围内快速下降,在大范围内缓慢地下降,因此当变量非常不均匀时,它会在最优状态下振荡。
理想的情况是让每个输入值的范围大致在-1≤x(i)≤1或者是-0.5≤x(i)≤0.5,但是该范围并不是严格要求的,目的是让所有输入变量都在类似的范围内即可。例如-3到3也是能接受的。
特征缩放
输入值/(所有输入值中最大与最小之差)
均值归一化
(输入值-输入值的平均值)/(所有输入值中最大与最小之差)
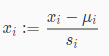
5 正规方程
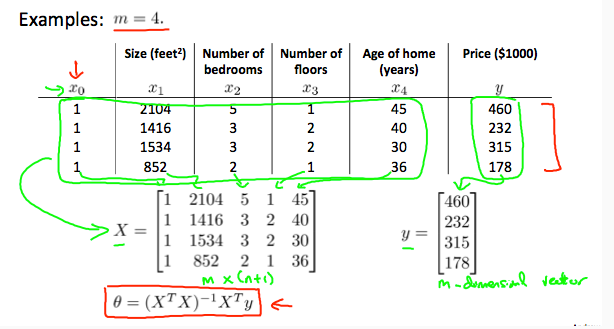
除了采用梯度下降来使代价函数最小,还可以通过正规方程的方法。即求出倒数令其为0,从而略去迭代过程。计算出的结果为

例子如下:
一维情况下,对每个theta求导,令倒数为0,求得使J(theta)最小的theta值

如下,首先要对数据进行矩阵构造,构造后的X的维度为m*(n+1),theta为(n+1)*1,y为m*1
关于梯度下降和正规方程的优缺对比:
|
Gradient Descent |
Normal Equation |
| 需要选择合适的学习效率 | 不需要选择学习效率 |
| 需迭代 | 无需迭代 |
| 计算复杂度为O(kn2) | 因为要计算XTX,计算复杂度为O(n3) |
| 当n比较大的时候仍能很好工作 | 当n比较大的时候,速度很慢 |
当XTX不可逆时该怎么办?
通常有两种原因,一是因为特征冗余,例如输入的两组数据线相关,可删除其中一个;二是特征太多(m≤n),可删除一些特征
Lecture 6
6 逻辑回归分类器
如果使用线性回归进行分类,将数值≥0.5的预测映射为1,反之为0,实际上效果并不好,因为分类并不一定是一个线性函数,因此本节主要讲的内容为logistic regression,之所以称之为logistic是因为hypothesis函数使用了logistic函数也可称为sigmoid函数。该函数的主要作用是将输出限定在0到1之间。函数形式如下所示:

函数形状如下: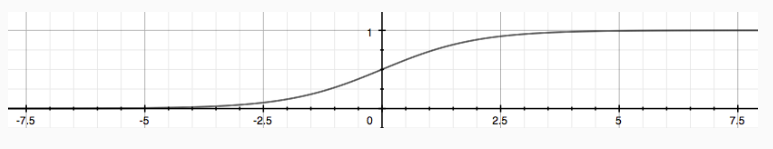
有一些公式的意思如下,在参数theta,给性x的情况下,y=1的概率表示为

逻辑回归的模型 是一个非线性模型,sigmoid函数,又称逻辑回归函数。但是它本质上又是一个线性回归模型,因为除去sigmoid映射函数关系,其他的步骤,算法都是线性回归的。可以说,逻辑回归,都是以线性回归为理论支持的。只不过,线性模型,无法做到sigmoid的非线性形式,sigmoid可以轻松处理0/1分类问题。
代价函数
线性回归中的代价函数已经不再适用于逻辑回归中,因为sigmoid函数将造成输出振荡,具有多个局部最小值,即“非凸”。逻辑回归中选用的代价函数如下:
可将代价函数合并为
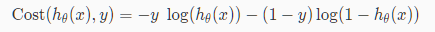

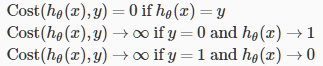
该代价函数保证了逻辑回归中J(θ)的凸性质。
则J(θ)为

向量化的表示为
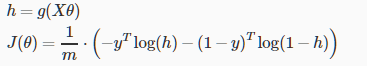
通用的梯度下降方法为
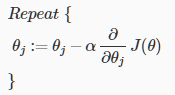
应用到逻辑回归中如下
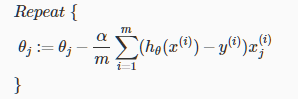
其他优化算法
除了梯度下降,还可以使用一些其他的优化算法:例如共轭梯度、BFGS、L-BFGS。相比梯度下降,这些方法不需要人为的选择学习效率,可以认为这些方法中有智能内循环,称之为线搜索算法来选择α。通常这些算法比梯度下降速度更快,但是缺点是复杂度比梯度下降高。
优化算法框架如下:

function [jVal, gradient] = costFunction(theta) jVal = [...code to compute J(theta)...]; gradient = [...code to compute derivative of J(theta)...]; end
接着使用fminunc()函数
options = optimset('GradObj', 'on', 'MaxIter', 100);
initialTheta = zeros(2,1);
[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);
多分类:一对多
此时y的输出值不再是0或1,而是0到n,将多分类问题分解成n+1个二分类问题,预测y是其中某一类的概率
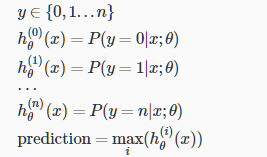


Lecture 7
7 正则化
- 欠拟合/高偏差 underfitting
- just right
- 过拟合/高方差 overfitting 泛化能力差
解决过拟合的方法
1) Reduce the number of features:
- Manually select which features to keep.
- Use a model selection algorithm (studied later in the course).
2) Regularization
- Keep all the features, but reduce the magnitude of parameters \theta_jθj.
- Regularization works well when we have a lot of slightly useful features.
举个例子
例如我们想要下述式子更趋向于二次函数: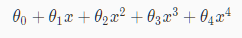
则要减少三次项和四此项的值,则我们在代价函数中增加:
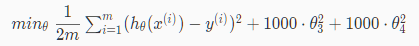
要使代价函数最小趋向于0,则需降低θ3和θ4的值,因为二次项≥0,所以令它们为0时代价函数最小,从而降低了他们在hypothesis function的影响,从而减少了过拟合。这就是正则化的思想,不用删减某一特征。

可将上述过程归纳为:

λ是正则化参数,当该参数选择过大时可能会引起欠拟合

线性回归的正则化

可将上述第二个式子重新表示成
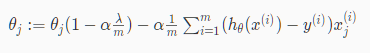
学习效率是一个比较小的数,因此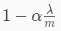 是一个比1小但很接近1的数。第二项和以前的线性回归中一样。
是一个比1小但很接近1的数。第二项和以前的线性回归中一样。
除了梯度下降,通过正规方程如下:
矩阵L的维度为(n+1)*(n+1),当m(样本数)<n(特征数)时,矩阵XTX是不可逆的,但加上λL后,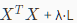 可逆
可逆
logistic 回归的正则化
逻辑回归的代价函数为: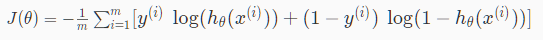
加上正则项

注意正则项都是从θ1开始的,没有对θ0进行惩罚。

与线性回归不同的是h函数不同。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号