[转]压缩感知重构算法之分段正交匹配追踪(StOMP)
分段正交匹配追踪(StagewiseOMP)或者翻译为逐步正交匹配追踪,它是OMP另一种改进算法,每次迭代可以选择多个原子。此算法的输入参数中没有信号稀疏度K,因此相比于ROMP及CoSaMP有独到的优势。
1、StOMP重构算法流程:
分段正交匹配追踪(StagewiseOMP)或者翻译为逐步正交匹配追踪,它是OMP另一种改进算法,每次迭代可以选择多个原子。此算法的输入参数中没有信号稀疏度K,因此相比于ROMP及CoSaMP有独到的优势。
1、StOMP重构算法流程:



2、分段正交匹配追踪(StOMP)Matlab代码(CS_StOMP.m)
function [ theta ] = CS_StOMP( y,A,S,ts )
%CS_StOMP Summary of this function goes here
%Version: 1.0 written by jbb0523 @2015-04-29
% Detailed explanation goes here
% y = Phi * x
% x = Psi * theta
% y = Phi*Psi * theta
% 令 A = Phi*Psi, 则y=A*theta
% S is the maximum number of StOMP iterations to perform
% ts is the threshold parameter
% 现在已知y和A,求theta
% Reference:Donoho D L,Tsaig Y,Drori I,Starck J L.Sparse solution of
% underdetermined linear equations by stagewise orthogonal matching
% pursuit[J].IEEE Transactions on Information Theory,2012,58(2):1094—1121
if nargin < 4
ts = 2.5;%ts范围[2,3],默认值为2.5
end
if nargin < 3
S = 10;%S默认值为10
end
[y_rows,y_columns] = size(y);
if y_rows<y_columns
y = y';%y should be a column vector
end
[M,N] = size(A);%传感矩阵A为M*N矩阵
theta = zeros(N,1);%用来存储恢复的theta(列向量)
Pos_theta = [];%用来迭代过程中存储A被选择的列序号
r_n = y;%初始化残差(residual)为y
for ss=1:S%最多迭代S次
product = A'*r_n;%传感矩阵A各列与残差的内积
sigma = norm(r_n)/sqrt(M);%参见参考文献第3页Remarks(3)
Js = find(abs(product)>ts*sigma);%选出大于阈值的列
Is = union(Pos_theta,Js);%Pos_theta与Js并集
if length(Pos_theta) == length(Is)
if ss==1
theta_ls = 0;%防止第1次就跳出导致theta_ls无定义
end
break;%如果没有新的列被选中则跳出循环
end
%At的行数要大于列数,此为最小二乘的基础(列线性无关)
if length(Is)<=M
Pos_theta = Is;%更新列序号集合
At = A(:,Pos_theta);%将A的这几列组成矩阵At
else%At的列数大于行数,列必为线性相关的,At'*At将不可逆
if ss==1
theta_ls = 0;%防止第1次就跳出导致theta_ls无定义
end
break;%跳出for循环
end
%y=At*theta,以下求theta的最小二乘解(Least Square)
theta_ls = (At'*At)^(-1)*At'*y;%最小二乘解
%At*theta_ls是y在At列空间上的正交投影
r_n = y - At*theta_ls;%更新残差
if norm(r_n)<1e-6%Repeat the steps until r=0
break;%跳出for循环
end
end
theta(Pos_theta)=theta_ls;%恢复出的theta
end
3、StOMP单次重构测试代码
以下测试代码基本与OMP单次重构测试代码一样,除了调用CS_StOMP之外,一定要注意这里的测量矩阵Phi =randn(M,N)/sqrt(M),一定一定!!!
%压缩感知重构算法测试
clear all;close all;clc;
M = 64;%观测值个数
N = 256;%信号x的长度
K = 12;%信号x的稀疏度
Index_K = randperm(N);
x = zeros(N,1);
x(Index_K(1:K)) = 5*randn(K,1);%x为K稀疏的,且位置是随机的
Psi = eye(N);%x本身是稀疏的,定义稀疏矩阵为单位阵x=Psi*theta
Phi = randn(M,N)/sqrt(M);%测量矩阵为高斯矩阵
A = Phi * Psi;%传感矩阵
y = Phi * x;%得到观测向量y
%% 恢复重构信号x
tic
theta = CS_StOMP(y,A);
x_r = Psi * theta;% x=Psi * theta
toc
%% 绘图
figure;
plot(x_r,'k.-');%绘出x的恢复信号
hold on;
plot(x,'r');%绘出原信号x
hold off;
legend('Recovery','Original')
fprintf('\n恢复残差:');
norm(x_r-x)%恢复残差
运行结果如下:(信号为随机生成,所以每次结果均不一样)
1)图:
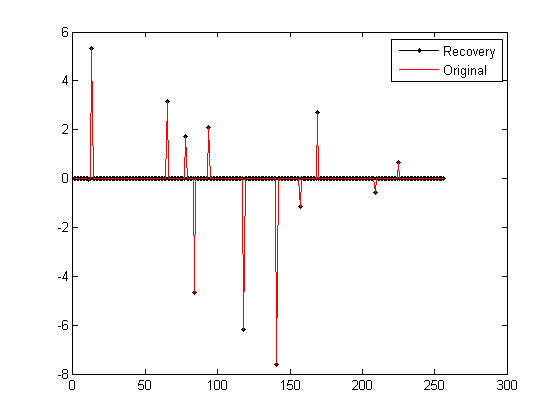
2)Command windows
Elapsedtime is 0.067904 seconds.
恢复残差:
ans=
6.1267e-015
4、门限参数ts、测量数M与重构成功概率关系曲线绘制例程代码
clear all;close all;clc;
%% 参数配置初始化
CNT = 1000;%对于每组(K,M,N),重复迭代次数
N = 256;%信号x的长度
Psi = eye(N);%x本身是稀疏的,定义稀疏矩阵为单位阵x=Psi*theta
ts_set = 2:0.2:3;
K_set = [4,12,20,28,36];%信号x的稀疏度集合
Percentage = zeros(N,length(K_set),length(ts_set));%存储恢复成功概率
%% 主循环,遍历每组(ts,K,M,N)
tic
for tt = 1:length(ts_set)
ts = ts_set(tt);
for kk = 1:length(K_set)
K = K_set(kk);%本次稀疏度
%M没必要全部遍历,每隔5测试一个就可以了
M_set=2*K:5:N;
PercentageK = zeros(1,length(M_set));%存储此稀疏度K下不同M的恢复成功概率
for mm = 1:length(M_set)
M = M_set(mm);%本次观测值个数
fprintf('ts=%f,K=%d,M=%d\n',ts,K,M);
P = 0;
for cnt = 1:CNT %每个观测值个数均运行CNT次
Index_K = randperm(N);
x = zeros(N,1);
x(Index_K(1:K)) = 5*randn(K,1);%x为K稀疏的,且位置是随机的
Phi = randn(M,N)/sqrt(M);%测量矩阵为高斯矩阵
A = Phi * Psi;%传感矩阵
y = Phi * x;%得到观测向量y
theta = CS_StOMP(y,A,10,ts);%恢复重构信号theta
x_r = Psi * theta;% x=Psi * theta
if norm(x_r-x)<1e-6%如果残差小于1e-6则认为恢复成功
P = P + 1;
end
end
PercentageK(mm) = P/CNT*100;%计算恢复概率
end
Percentage(1:length(M_set),kk,tt) = PercentageK;
end
end
toc
save StOMPMtoPercentage1000 %运行一次不容易,把变量全部存储下来
%% 绘图
for tt = 1:length(ts_set)
S = ['-ks';'-ko';'-kd';'-kv';'-k*'];
figure;
for kk = 1:length(K_set)
K = K_set(kk);
M_set=2*K:5:N;
L_Mset = length(M_set);
plot(M_set,Percentage(1:L_Mset,kk,tt),S(kk,:));%绘出x的恢复信号
hold on;
end
hold off;
xlim([0 256]);
legend('K=4','K=12','K=20','K=28','K=36');
xlabel('Number of measurements(M)');
ylabel('Percentage recovered');
title(['Percentage of input signals recovered correctly(N=256,ts=',...
num2str(ts_set(tt)),')(Gaussian)']);
end
for kk = 1:length(K_set)
K = K_set(kk);
M_set=2*K:5:N;
L_Mset = length(M_set);
S = ['-ks';'-ko';'-kd';'-kv';'-k*';'-k+'];
figure;
for tt = 1:length(ts_set)
plot(M_set,Percentage(1:L_Mset,kk,tt),S(tt,:));%绘出x的恢复信号
hold on;
end
hold off;
xlim([0 256]);
legend('ts=2.0','ts=2.2','ts=2.4','ts=2.6','ts=2.8','ts=3.0');
xlabel('Number of measurements(M)');
ylabel('Percentage recovered');
title(['Percentage of input signals recovered correctly(N=256,K=',...
num2str(K),')(Gaussian)']);
end
程序运行结束会出现6+5=11幅图,前6幅图分别是ts分别为2.0、2.2、2.4、2.6、2.8和3.0时的测量数M与重构成功概率关系曲线(类似于OMP此部分,这里只是对每一个不同的ts画出一幅图),后5幅图是分别将稀疏度K为4、12、20、28、32时将六种ts取值的测量数M与重构成功概率关系曲线绘制在一起以比较ts对重构结果的影响。
对于前6幅图这里只给出ts=2.4时的曲线图:
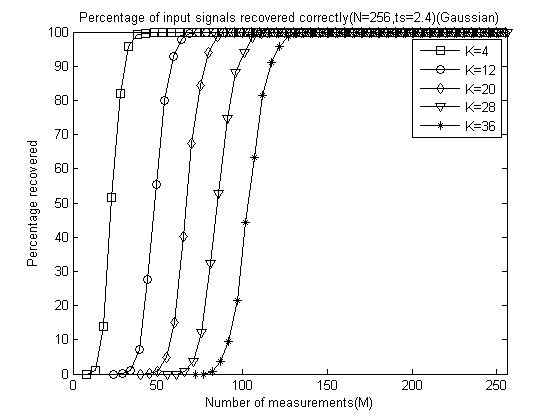
对于后5幅图这里全部给出,为了清楚地看出ts的影响,这里把图的横轴拉伸:
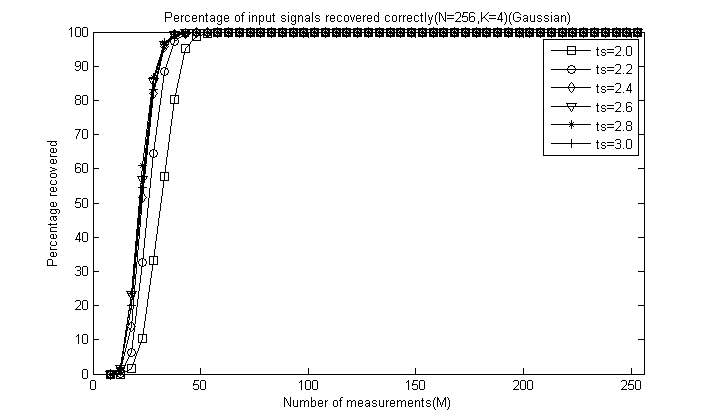

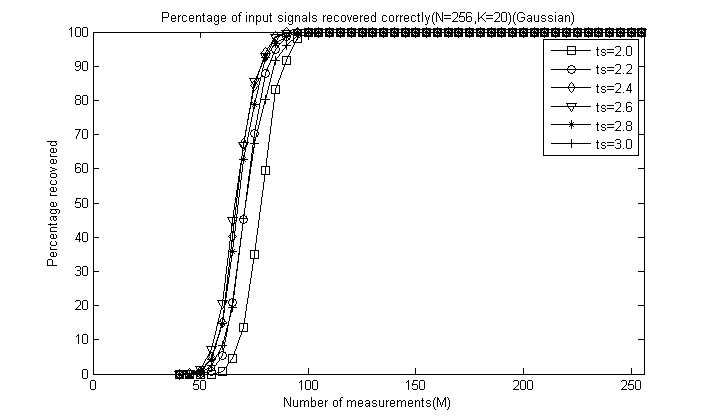

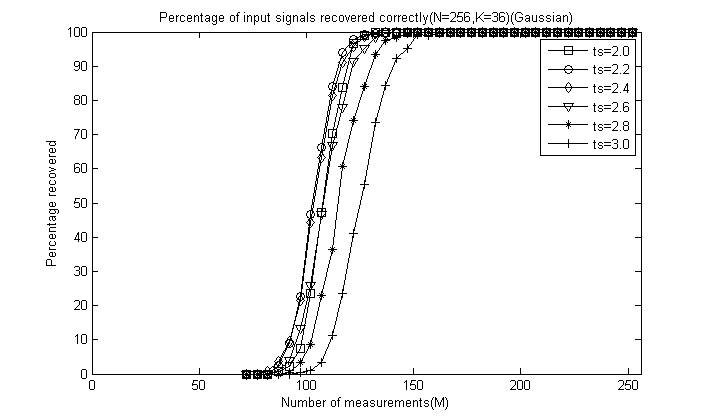
通过对比可以看出,总体上讲ts=2.4或ts=2.6时效果较好,较大和较小重构效果都会降低,这里由于没有ts=2.5的情况,但我们推测ts=2.5应该是一个比较好的值,因此一般默认取为2.5即可。
5、结语
有关StOMP的流程图可参见文献[1]的Fig.1:
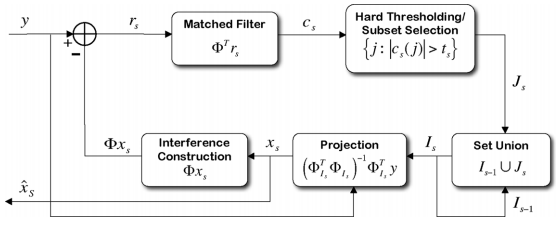
有关StOMP门限的选取在文献[1]中也有提及:
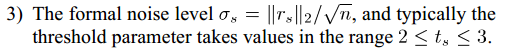
关于这个门限的来源文献[1]有也有一个推导,注意推导过程中的N(0,1/n):
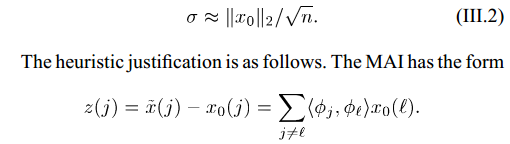

尽管StOMP输入参数中不需要信号的稀疏度,但门限设置与测量矩阵有密切的关系,文献[1]中的门限也只适用于随机高斯矩阵而己,因此限制了此算法的应用。
参考文献:
[1] Donoho D L,Tsaig Y,DroriI,Starck J L.Sparsesolution of underdetermined linear equations by stagewise orthogonal matchingpursuit[J].IEEE Transactions on InformationTheory,2012,58(2):1094—1121.


