压缩感知重构算法之正则化正交匹配追踪(ROMP)
在看代码之前，先拜读了ROMP的经典文章：Needell D，VershyninR．Signal recovery from incompleteand inaccurate measurements via regularized orthogonal matching pursuit[J]. IEEEJournal on Selected Topics in Signal Processing, 2010, 4(2): 310—316.
看完一脸懵逼，真的没看懂啥，虽然页数不多，在下文中就单纯的借鉴文章中的算法流程。
正交匹配追踪算法每次迭代均只选择与残差最相关的一列，自然人们会想：“每次迭代是否可以多选几列呢?”，正则化正交匹配追踪(RegularizedOMP)就是其中一种改进方法。本篇将在上一篇《压缩感知重构算法之正交匹配追踪(OMP)》的基础上给出正则化正交匹配追踪(ROMP)算法的MATLAB函数代码，并且给出单次测试例程代码、测量数M与重构成功概率关系曲线绘制例程代码。
0、符号说明如下
压缩观测y=Φx，其中y为观测所得向量M×1，x为原信号N×1（M<<N）。x一般不是稀疏的，但在某个变换域Ψ是稀疏的，即x=Ψθ，其中θ为K稀疏的，即θ只有K个非零项。此时y=ΦΨθ，令A=ΦΨ，则y=Aθ。
(1) y为观测所得向量，大小为M×1
(2) x为原信号，大小为N×1
(3) θ为K稀疏的，是信号在x在某变换域的稀疏表示
(4) Φ称为观测矩阵、测量矩阵、测量基，大小为M×N
(5) Ψ称为变换矩阵、变换基、稀疏矩阵、稀疏基、正交基字典矩阵，大小为N×N
(6) A称为测度矩阵、传感矩阵、CS信息算子，大小为M×N
上式中，一般有K<<M<<N，后面三个矩阵各个文献的叫法不一，以后我将Φ称为测量矩阵、将Ψ称为稀疏矩阵、将A称为传感矩阵。
1、ROMP重构算法流程
正则化正交匹配追踪算法流程与OMP的最大不同之处就在于从传感矩阵A中选择列向量的标准，OMP每次只选择与残差内积绝对值最大的那一列，而ROMP则是先选出内积绝对值最大的K列（若所有内积中不够K个非零值则将内积值非零的列全部选出），然后再从这K列中按正则化标准再选择一遍，即为本次迭代选出的列向量（一般并非只有一列）。正则化标准意思是选择各列向量与残差内积绝对值的最大值不能比最小值大两倍以上(comparable coordinates)且能量最大的一组(with the maximal energy)，因为满足条件的子集并非只有一组。似乎用叙述语言描述不清楚，下面给出一种实现第(2)(3)步的算法流程图：
贴出文献[1]中的算法流程：
看完论文后对算法的理解并不是很深入，下面结合博客中的算法流程来对ROMP算法流程进行解释。上述流程图讲的是正则化的过程，最多经过K次迭代可选出全部所需的原子。在Identify中首先将所得到的内积值按降序排列，然计算内积中非零元素的个数，然后选取前K个内积值或者所有非零值（也就是论文中提到的选择集合比较小的那个），记录选取的内积值所对应的列序号，构成集合J，相应的内积值构成集合Jval。
正则化的过程结合代码来解释。
function[val,pos]=Regularize(product,Kin)
% Regularize Summary of this function goes here
% Detailed explanation goes here
% product = A'*r_n;%传感矩阵A各列与残差的内积
% K为稀疏度
% pos为选出的各列序号
% val为选出的各列与残差的内积值
% Reference:Needell D，Vershynin R. Uniform uncertainty principle and
% signal recovery via regularized orthogonal matching pursuit.
% Foundations of Computational Mathematics, 2009,9(3): 317-334.
productabs=abs(product);%取绝对值
[productdes,indexproductdes]=sort(productabs,'descend');%降序排列
for ii=length(productdes):-1:1
if productdes(ii)>1e-6%判断productdes中非零值个数
break;
end
end
%Identify:Choose a set J of the K biggest coordinates
if ii>=Kin
J=indexproductdes(1:Kin);%集合J
Jval=productdes(1:Kin);%集合J对应的序列值
K=Kin;
else%or all of its nonzero coordinates,whichever is smaller
J=indexproductdes(1:ii);%集合J
Jval=productdes(1:ii);%集合J对应的序列值
K=ii;
end
%Regularize:Among all subsets J0∈J with comparable coordinates
MaxE=-1;%循环过程中存储最大能量值
for kk=1:K
J0_tmp=zeros(1,K);iJ0=1;
J0_tmp(iJ0)=J(kk);%以J(kk)为本次寻找J0的基准(最大值)
Energy=Jval(kk)^2;%本次寻找J0的能量
for mm=kk+1:K
if Jval(kk)<2*Jval(mm)%找到符合|u(i)|<=2|u(j)|的
iJ0=iJ0+1;%J0自变量增1
J0_tmp(iJ0)=J(mm);%更新J0
Energy=Energy+Jval(mm)^2;%更新能量
else%不符合|u(i)|<=2|u(j)|的
break;%跳出本轮寻找，因为后面更小的值也不会符合要求
end
end
if Energy>MaxE%本次所得J0的能量大于前一组
J0=J0_tmp(1:iJ0);%更新J0
MaxE=Energy;%更新MaxE，为下次循环做准备
end
end
pos=J0;
val=productabs(J0);
end
第12行代码中用到了函数sort进行排序，采用的是降序方式，indexproductdes索引中保存的是排序后的内积值productdes在原来集合productabs中原来所在的位置。
第13-17行判断大于0的内积值的个数，并在第19到27行中进行选择，将内积值所对应的列序号形成集合J，并将所选择的内积值组成集合Jval。
第29行，首先初始化 MaxE为-1.
第30行，接下来是在第某次选择出的J中选择子集J0 ，总共迭代K次，K为原始信号非零元素的个数。
接着聊聊如何选择J0 ，首先选择Jval（kk）（为与K区分，选用与代码中一样的kk形式）为基准，初始化m=kk，然后遍历m+1即（k+1，也就是此次k的下一个内积值）到K，判断Jval(kk)<=2*Jval(mm)，也就是论文中所说的|u(i)|<=2|u(j)|，这个地方想了很久，然后去运行代码调试才搞明白。这里先假设我已经找到了能量最大的一组。然后我选择出来的J0 所包含的列向量的序号有此次的k，还有满足Jval(kk)<=2*Jval(mm)的mm，在代码中开始已经将J（kk）的值赋给了J0_tmp(iJ0)（初始iJ0=1），也就是代码的第32行，后续满足条件的J（mm）也分别赋值给了J0_tmp（iJ0）（iJ0=iJ0+1），所以最后的J0 =J0_tmp(1:iJ0)（也就是初始的基准Jval（kk）和后面满足条件的m），在流程图中J0=J（1：m），我觉得这是不够严谨的，一开始想了很久想不明白，难道变换的只是m而已吗，所以我觉得在这里是不太正确的。
另外仔细观察论文中的这一项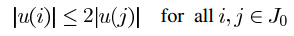
，也是困扰了我很久的地方，注意这里的u（i）相当于此次我们的Jval（k），u（j）是我们要遍历判断的，最后i，j都是属于J0的，所以也说明了上一段J0所应包含的列向量序号的集合。
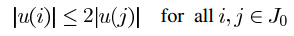，也是困扰了我很久的地方，注意这里的u（i）相当于此次我们的Jval（k），u（j）是我们要遍历判断的，最后i，j都是属于J0的，所以也说明了上一段J0所应包含的列向量序号的集合。 接着说明J0的选择，应该是在所有满足条件的J的子集中能量最大的一组，第43到46行进行了能量的比较，如果能量比上一次的能量大才会进行J0的赋值，否则进入下一次循环直至结束。到这里一次的J0选择完毕。
2、正则化正交匹配追踪(ROMP)MATLAB代码(CS_ROMP.m)
这个函数是完全基于上一篇中的CS_OMP.m修改而成的。
function [ theta ] = CS_ROMP( y,A,K )
%CS_ROMP Summary of this function goes here
%Version: 1.0 written by jbb0523 @2015-04-24
% Detailed explanation goes here
% y = Phi * x
% x = Psi * theta
% y = Phi*Psi * theta
% 令 A = Phi*Psi, 则y=A*theta
% 现在已知y和A，求theta
% Reference:Needell D，Vershynin R．Signal recovery from incomplete and
% inaccurate measurements via regularized orthogonal matching pursuit[J]．
% IEEE Journal on Selected Topics in Signal Processing，2010，4(2)：310—316.
[y_rows,y_columns] = size(y);
if y_rows<y_columns
y = y';%y should be a column vector
end
[M,N] = size(A);%传感矩阵A为M*N矩阵
theta = zeros(N,1);%用来存储恢复的theta(列向量)
At = zeros(M,3*K);%用来迭代过程中存储A被选择的列
Pos_theta = zeros(1,2*K);%用来迭代过程中存储A被选择的列序号
Index = 0;
r_n = y;%初始化残差(residual)为y
%Repeat the following steps K times(or until |I|>=2K)
for ii=1:K%迭代K次
product = A'*r_n;%传感矩阵A各列与残差的内积
%[val,pos] = max(abs(product));%找到最大内积绝对值，即与残差最相关的列
[val,pos] = Regularize(product,K);%按正则化规则选择原子
At(:,Index+1:Index+length(pos)) = A(:,pos);%存储这几列
Pos_theta(Index+1:Index+length(pos)) = pos;%存储这几列的序号
if Index+length(pos)<=M%At的行数大于列数，此为最小二乘的基础(列线性无关)
Index = Index+length(pos);%更新Index，为下次循环做准备
else%At的列数大于行数，列必为线性相关的,At(:,1:Index)'*At(:,1:Index)将不可逆
break;%跳出for循环
end
A(:,pos) = zeros(M,length(pos));%清零A的这几列(其实此行可以不要因为它们与残差正交)
%y=At(:,1:Index)*theta，以下求theta的最小二乘解(Least Square)
theta_ls = (At(:,1:Index)'*At(:,1:Index))^(-1)*At(:,1:Index)'*y;%最小二乘解
%At(:,1:Index)*theta_ls是y在At(:,1:Index)列空间上的正交投影
r_n = y - At(:,1:Index)*theta_ls;%更新残差
if norm(r_n)<1e-6%Repeat the steps until r=0
break;%跳出for循环
end
if Index>=2*K%or until |I|>=2K
break;%跳出for循环
end
end
theta(Pos_theta(1:Index))=theta_ls;%恢复出的theta
end
相比CS_OMP.m，ROMP所做的修改已用颜色标出。
首先解释下第19行和20行，博客中的解释是：
然后我还是没有太明白，但是传感矩阵满足2K阶RIP，满足2K阶RIP的矩阵任意2K列线性无关。可能跟这个有关系，以后再看看。
接着是第21行，为什么索引值Index不直接设置为1呢，每次选择的原子有可能为几列，则这次所选择出来的原子存放的位置，应该从上次存放的最后一列的位置+1到这次所选择的原子长度加上上次存放的最后一列的位置。比如第一次存放的位置应该为0+1：0+length（pos），下一次存放的位置表示为Index+1：Index+length(pos)。
继续解释第30到33行，这里是判断我们所选择出的原子构成的矩阵At行数与列数比较的关系。At选择的列向量都是非零的，也就是说At是列满秩的矩阵。（列满秩就是列秩等于列数,就是初等变换以后没有一列全为0. 满秩矩阵是一个很重要的概念, 它是判断一个矩阵是否可逆的充分必要条件）看了下线性代数，还没有看懂。。。
第40行到第44行是对循环结束条件的判断，或者残差小于一定范围，或者是索引集合Index>=2K。
3、ROMP单次重构测试代码
以下测试代码与上一篇中的OMP单次测试代码基本完全一致，除了M和K参数设置及调用CS_ROMP函数三处之外。
%压缩感知重构算法测试
clear all;close all;clc;
M=128;%观测值个数
N=256;%信号x的长度
K=12;%信号x的稀疏度
Index_K=randperm(N);
x=zeros(N,1);
x(Index_K(1:K))=5*randn(K,1);%x为K稀疏的，且位置是随机的
Psi=eye(N);%x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
Phi=randn(M,N);%测量矩阵为高斯矩阵
A=Phi*Psi;%传感矩阵
y=Phi*x;%得到观测向量y
%% 恢复重构信号x
tic
theta=CS_ROMP(y,A,K);
x_r=Psi*theta;% x=Psi * theta
toc
%% 绘图
figure;
plot(x_r,'k.-');%绘出x的恢复信号
hold on;
plot(x,'r');%绘出原信号x
hold off;
legend('Recovery','Original')
fprintf('\n恢复残差：');
norm(x_r-x)%恢复残差
运行结果如下：（信号为随机生成，所以每次结果均不一样）
1）图：
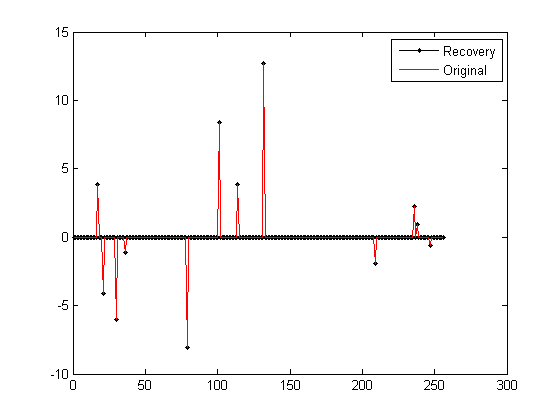
2）Commandwindows
Elapsedtime is 0.022132 seconds.
恢复残差：
ans=
7.8066e-015
4、测量数M与重构成功概率关系曲线绘制例程代码
以下测试代码与上一篇中的OMP测量数M与重构成功概率关系曲线绘制例程代码基本完全一致。本程序在循环中填加了“kk”一行代码并将“M = M_set(mm)”一行的分号去掉，这是为了在运行过程中可以观察程序运行状态、知道程序到哪一个位置。
clear all;close all;clc;
%% 参数配置初始化
CNT=1000;%对于每组(K,M,N)，重复迭代次数
N=256;%信号x的长度
Psi=eye(N);%x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
K_set=[4,12,20,28,36];%信号x的稀疏度集合
Percentage=zeros(length(K_set),N);%存储恢复成功概率
%% 主循环，遍历每组(K,M,N)
tic
forkk=1:length(K_set)
K=K_set(kk);%本次稀疏度
M_set=K:5:N;%M没必要全部遍历，每隔5测试一个就可以了
PercentageK=zeros(1,length(M_set));%存储此稀疏度K下不同M的恢复成功概率
kk
formm=1:length(M_set)
M=M_set(mm)%本次观测值个数
P=0;
forcnt=1:CNT%每个观测值个数均运行CNT次
Index_K=randperm(N);
x=zeros(N,1);
x(Index_K(1:K))=5*randn(K,1);%x为K稀疏的，且位置是随机的的
Phi=randn(M,N);%测量矩阵为高斯矩阵
A=Phi*Psi;%传感矩阵
y=Phi*x;%得到观测向量y
theta=CS_ROMP(y,A,K);%恢复重构信号theta
x_r=Psi*theta;% x=Psi * theta
ifnorm(x_r-x)<1e-6%如果残差小于1e-6则认为恢复成功
P=P+1;
end
end
PercentageK(mm)=P/CNT*100;%计算恢复概率
end
Percentage(kk,1:length(M_set))=PercentageK;
end
toc
save ROMPMtoPercentage1000%运行一次不容易，把变量全部存储下来
%% 绘图
S=['-ks';'-ko';'-kd';'-kv';'-k*'];
figure;
forkk=1:length(K_set)
K=K_set(kk);
M_set=K:5:N;
L_Mset=length(M_set);
plot(M_set,Percentage(kk,1:L_Mset),S(kk,:));%绘出x的恢复信号
hold on;
end
hold off;
xlim([0256]);
legend('K=4','K=12','K=20','K=28','K=36');
xlabel('Number of measurements(M)');
ylabel('Percentage recovered');
title('Percentage of input signals recovered correctly(N=256)(Gaussian)');
本程序运行结果：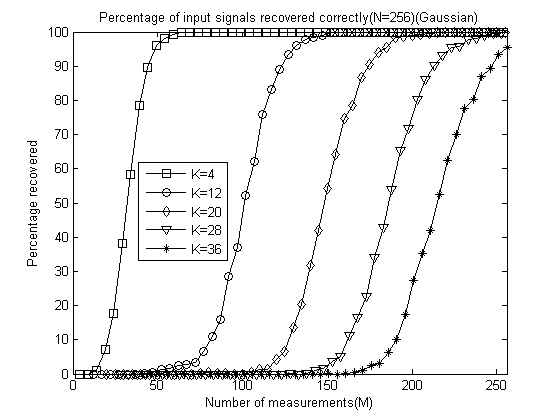
参考文献：
[1] Needell D，VershyninR．Signal recovery from incompleteand inaccurate measurements via regularized orthogonal matching pursuit[J]. IEEEJournal on Selected Topics in Signal Processing, 2010, 4(2): 310—316.
