有限等距性质RIP

参考博客：http://blog.csdn.net/jbb0523/article/details/44565647

压缩感知测量矩阵之有限等距性质（Restricted Isometry Property,RIP）

---

》定义

   不同的文献对RIP定义的表达不同，详细可参考博客中的定义，在这里选取一种自己比较能理解的定义，如下所示：

  

---

！！！重点，RIP是对哪一个矩阵的约束？

   在没参考这篇博客之前，阅读了师兄的论文，之前一直以为是对观测矩阵的约束，然而事实是RIP是对传感矩阵的约束，传感矩阵即观测矩阵与表示矩阵的乘积所构成的矩阵，又称为字典。

   压缩观测y=Φx，其中y为观测所得向量M×1，x为原信号N×1（M<<N）。x一般不是稀疏的，但在某个变换域Ψ是稀疏的，即x=Ψθ，其中θ为K稀疏的，即θ只有K个非零项。此时y=ΦΨθ，令A=ΦΨ，则y=Aθ。

        (1) y为观测所得向量，大小为M×1

        (2) x为原信号，大小为N×1

        (3) θ为K稀疏的，是信号在x在某变换域的稀疏表示

        (4) Φ称为观测矩阵、测量矩阵、测量基，大小为M×N

        (5) Ψ称为变换矩阵、变换基、稀疏矩阵、稀疏基、正交基字典矩阵，大小为N×N

        (6) A称为测度矩阵、传感矩阵、CS信息算子，大小为M×N

   上式中，一般有K<<M<<N，后面三个矩阵各个文献的叫法不一，以后我将Φ称为测量矩阵、将Ψ称为稀疏矩阵、将A称为传感矩阵。

   实际上RIP是针对传感矩阵A的。从定义中可知x是稀疏的，信号x一般时候都不是稀疏的，所以定义中RIP针对的矩阵不是y=Φx中的Φ，而是y=Aθ中的A，定义中的x实际上是这里的θ。

 

---

》如何理解RIP性质？

   1.能量说

   向量的2范数的平方就是信号的能量，换成常见的公式：

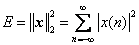
   这个公式可以数字信号处理教材中讲信号分类的章节找到，实际上将信号看成是电压信号或电流信号，这是在单位电阻上的能量（即u²t/R或i²t/R，R=1Ω，再离散即可）。

   这里将中文定义一中的RIP性质的不等式按刚才规定好的一套符号重新写出：

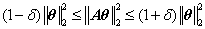
   这里的||Aθ||²₂实际上是||y||²₂，即输出信号的能量， ||θ||²₂即输入信号的能量（稀疏变换x=Ψθ为正交变换，而正交变换保持能量不变，即信号理论中的Parseval定理）。

   RIP其实可以看成刻画一个矩阵和标准正交阵的相似程度。其对于向量做变化后的 L2 能量（范数平方）相较于原向量的能量的变化不超过RIP。

   其实取极限当δ=0时（RIP要求0<δ<1），RIP的不等式实际上表示的是观测所得向量y的能量等于信号x的能量，在线性代数中所讲的正交变换也具有这种性质，也称为等距变换（把信号将为二维或三维时2范数的平方可形象的理解为到原点的距离），当然这里的变换因为传感矩阵A不可能是正交矩阵（不是方阵），但当极限δ=0时也能保持能量相等（也可以称为等距吧），而RIP要求0<δ<1，所以不可能等距，所以就称为有限等距性质吧。

 

   2.唯一映射说

   RIP性质（有限等距性质）保证了观测矩阵不会把两个不同的K稀疏信号映射到同一个集合中（保证原空间到稀疏空间的一一映射关系），要求从观测矩阵中抽取的每M个列向量构成的矩阵是非奇异的。

   文献[李树涛，魏丹.压缩传感综述[J]. 自动化学报，2009，35(11)：1369-1377.]中提到：

    “由于稀疏矩阵是固定的，要使得传感矩阵满足约束等距条件，可以通过设计测量矩阵解决”，RIP是针对传感矩阵的，但为什么我们确来研究测量矩阵呢？我想这就是答案了吧。这里还提到了“2K列都不相关”，其实这很好理解：如果矩阵有2K列线性相关，则对于某一个2K稀疏的信号必然会有Aθ_2K=0，又因为一个2K稀疏的信号可以写成两个K稀疏的信号相减（把2K稀疏信号的2K个非零项分成两部分，每部分分别包含K个非零项，其余部分填零长度与原2K稀疏信号保持不变，即得到了两个K稀疏信号，其中的一个K稀疏信号中的K个非零项乘负一，另一部分减这一部分必然等于2K稀疏信号），因此有A(θ_K1－θ_K2)=0，即Aθ_K1=Aθ_K2，也就是说对于两个不同的K稀疏信号θ_K1和θ_K2，压缩观测后得到了同一个y，即不能保证唯一映射，所以矩阵不能有2K列线性相关，否则将不能保证唯一映射。

 

   矩阵满足2K阶RIP保证了能够把任意一个K稀疏信号θ_K映射为唯一的y，也就是说要想通过压缩观测y恢复K稀疏信号θ_K，必须保证传感矩阵满足2K阶RIP，满足2K阶RIP的矩阵任意2K列线性无关。