【解题报告】 洛谷P1663 山

【解题报告】 洛谷P1663 山

题目描述

给出一座山，如图。

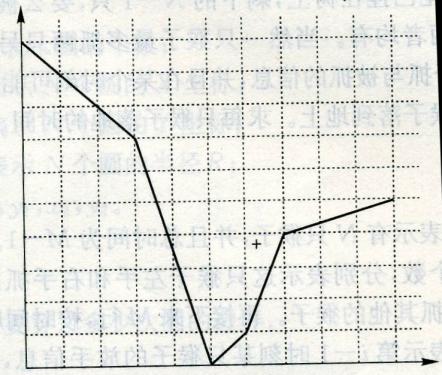
现在要在山上的某个部位装一盏灯，使得这座山的任何一个部位都能够被看到。

给出最小的y坐标，如图的+号处就是y坐标最小的安装灯的地方。

输入格式

第一行一个数N，表示这座山由N个点构成；

接下来N行从左到右给出了这座山的构造情况，每行两个数Xi、Yi，表示一个折点，保证Xi>Xi-1

输出格式

仅输出一行，为最小的y坐标，当你的答案与标准答案相差不超过0.01时，则被认为是正确的。

输入输出样例

输入 #1

6
0 0
10 0
11 1
15 1
16 0
25 0

输出 #1

3.00

说明/提示

数据规模：

30%的数据，\(1\le N\le 50\)

100%的数据，\(1\le N \le 5000 ,0\le X_i,Y_i\le 10^6\)，保证答案不超过\(10^6\)

思路

二分答案

读题，要在山上安装一个灯，让整个山都可以找到，说明这一盏灯和任意一个山的折点的连线和其他的山连成的线都不相交，由于题目会给出所有的折点的坐标，所以我们用一个初中二年级就学过的公式来求

\[y=kx+b(k、b为常数，k\ne0) \]

对于电脑来说，可以变形一下，变出以下两个式子

\[k_i=\frac{y_i-y_{i-1}} {x_i-x_{i-1}} \]

\[b_i=y_i-k_ix_i \]

这样就可以算出来所有线的解析式了，然后我们的答案一定要在所有线取\(max\)值的上方，即存在即可，枚举一下，复杂度为\(O(n^2)\)，n最大为5000，可以过，但是数据如果更大怎么办呢？

这个题目刚好就是求最大值最小的问题，所以我们可以使用二分答案，这样最终的复杂度就是\(O(n\log n)\)

代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
using namespace std;
const double eps=1e-3;
const int MAXN=5005;
int n;
double x[MAXN],y[MAXN],k[MAXN],b[MAXN];
double ans;
bool check(double x)
{
	double L=-2e9,R=2e9;
	for(int i=2;i<=n;i++)
	{
		if(k[i]<0) L=max(L,((x-b[i])/k[i]));
		else if(k[i]>0) R=min(R,((x-b[i])/k[i]));
		else if(x<b[i]) return false;
	}
	return L<=R;
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	cin>>x[i]>>y[i];
	for(int i=2;i<=n;i++)
	{
		k[i]=(y[i]-y[i-1])/(x[i]-x[i-1]);
		b[i]=y[i]-k[i]*x[i];
	}
	double l=0,r=1e9;
	while(eps<=r-l)
	{
		double mid=(l+r)/2;
		if(check(mid)) r=mid,ans=mid;
		else l=mid;
	}
	printf("%.2lf",ans);
	return 0;
}