骗分杂谈
前言:
因为在这篇博客之前,OI界还有一本 《骗分导论》,为了尊重前人,本博客不与其重名。
这几天的考试让我相当不适应。因为各种数据水,导致大家都用了奇怪的错解AC。
没错,数据水到可以贪心100分,\(n^2\)过十万。(这就是冲刺省选的多校联考模拟赛吗,i了)
分差拉大的背后,其实也反映出我的骗分能力不够。
因此本博客应运而生。
写这篇博客之前,我也先拜读了《骗分导论》。其实我并没有感到有太大帮助。
首先是文章中用了相当篇幅介绍的dfs,模拟之流,在我看来都不能归于“骗分”的范畴,而更多的属于“暴力”领域。
其次文章中当然也介绍了一些骗分的思想。但是可以看到,很多部分相当概括。大家都知道,如果追求覆盖面广的话,很可能会失去准确度。
然后,文章中举的绝大部分例题,都是相当基础的,对于具备一定水平的OIer来说,根本不需要骗分,也一样能够轻松拿到满分。这样的例题并不能让人感受到骗分的魅力和价值所在。
以上内容并没有在批判前人,而是要说明本篇的使命——用大量较有难度的例题,介绍具体的骗分方法,使读者打开思路。由于比较具体,很多方法其实是不能搬运到其他题目上的。重在打开思路。
当然也要注意到,骗分毕竟不是根本,它的局限性太大了,因此还是要多努力写代码,提升自己才是最有效的途径。
很重要的一点
我承认以上都是瞎编的
正文:
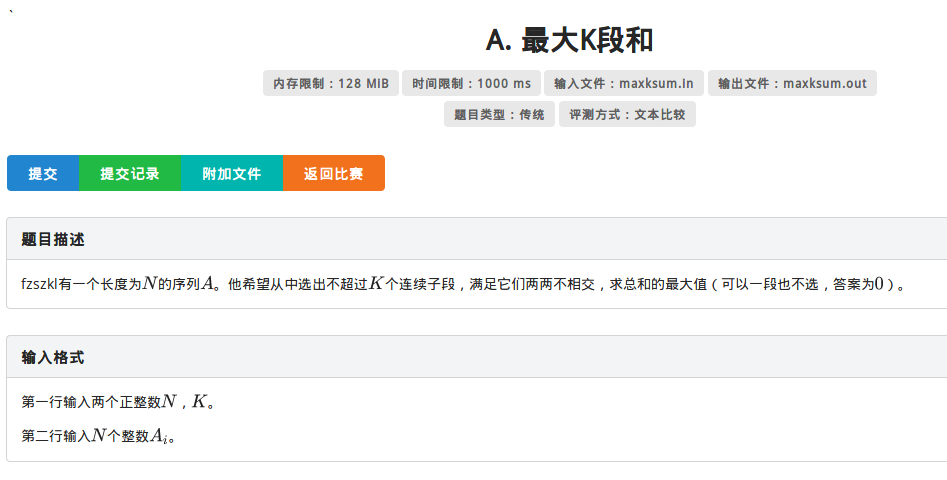
1.最大K段和(\(n^2\)过十万)
题面:

正解:
先简单说一下正解。
这题首先可以发现,如果要选某一段正数,那么一定要把连续的一段都选完,因为不要白不要。
负数也是要把连续的一段都选完,因为如果要选负数,当且仅当是因为想把这一段负数两边连接的两段正数连起来,如果负数不选连续的一段,那就没有意义了。
因此,第一步先把连续的正数(负数)都缩成一个点。此时正数负数一定是相间的。因为两边的数如果是负数,那么一定不选。因此去掉。
此时正数数量一定等于负数数量加一。
然后可以发现一个很重要的性质。
我们先假定选上了所有的正数。
此时如果不合法,一定是因为正数数量大于最多能选的段数了。
为了减少段数,可以考虑两种途径:
首先可以拿掉一个正数,这样显然可以减少一段
其次可以加上一段负数,这样相当于连接了两边的正数,等价于减少一段。
我们又可以发现,对于一对相邻的正负数,不可能同时拿掉正数,加上负数。因为这样是没有意义的。
因此转化成了一个经典的问题:luogu P1792 [国家集训队]种树
如果不会,这里推荐姚队的题解
骗分前提:
数据随机
骗分方法:
一.
注意到如果k大于等于正数段数量,那就相当与不用选负数。
于是把所有的正数加起来输出即可。
示例:

二.
注意到把连续的正(负)数缩到一起之后,最终序列长度可能会很小,此时可以跑&n^2&的简单dp。
因此缩完后可以特判一下,如果最后序列长度可以用\(n^2\)dp跑出来,那就跑\(n^2\)dp
这里有血淋淋的教训:
像这样最终数据规模上下界差距过大时(可能缩到1,也可能一个都缩不掉),要把判断范围写大一些,尽量卡住时空限制的边。
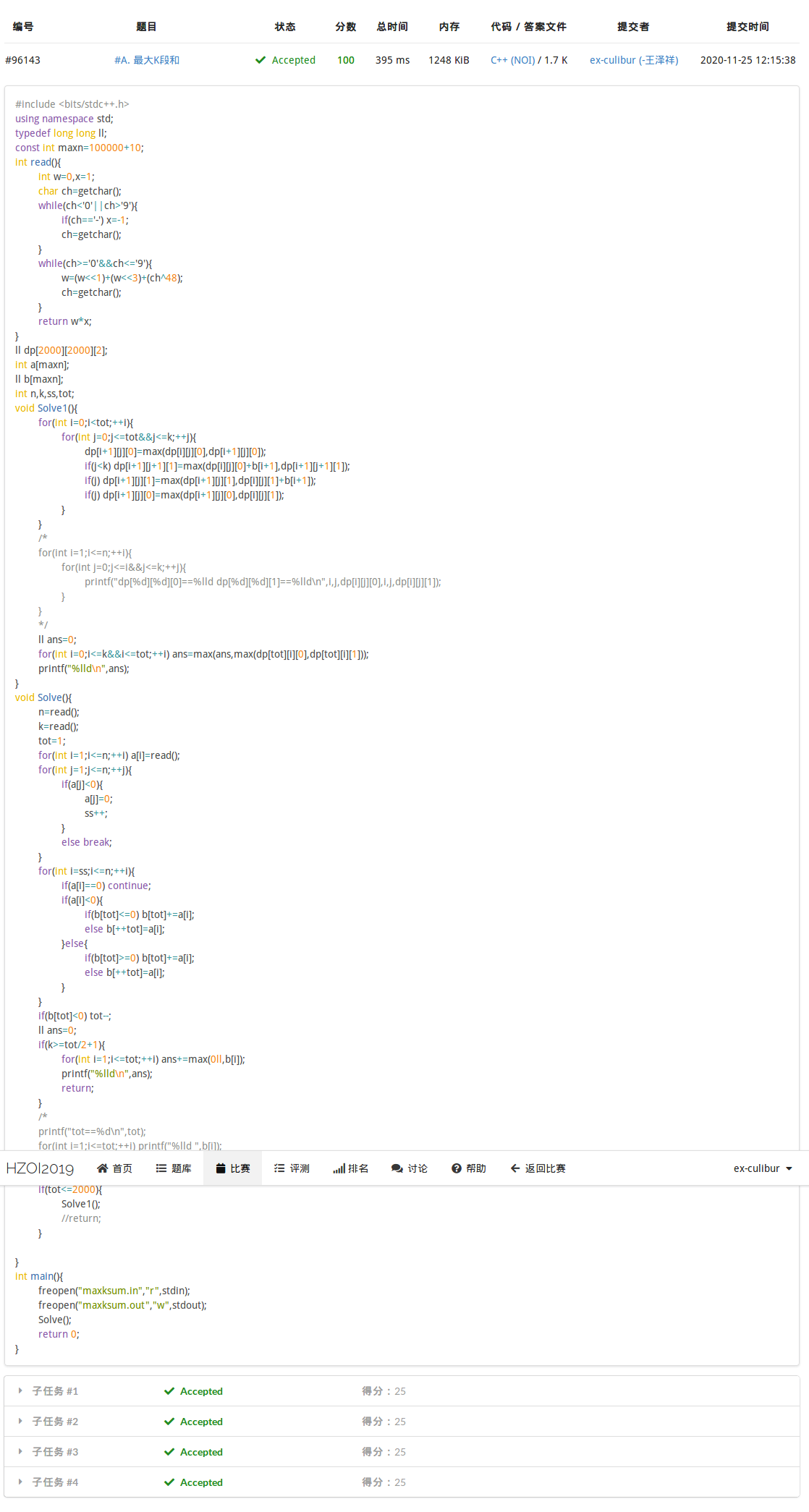
比如我,考试时把规模限制在1e3,拿了50分。后来换成2e3,直接AC。。。
示例:
2.CF505E Mr. Kitayuta vs. Bamboos
正解:
还不会,留坑。
骗分前提:
数据随机(模拟赛,数据自造的)
骗分方法:
注意到这题的难点在于对于某个竹子,可能会出现因为高度不够而无法砍掉p米的情况。
但是又注意到如果数据随机,这种情况很大可能不会出现。
因此在没有正解思路的情况下,就可以大胆地使用这个错误的贪心策略。
示例:
(用考试时的数据可以AC,考后才加的hack数据)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号