上午小测3 T1 括号序列 && luogu P5658 [CSP/S 2019 D1T2] 括号树 题解
前 言:
一直很想写这道括号树。。毕竟是在去年折磨了我4个小时的题。。。。
上午小测3 T1 括号序列
前言:
原来这题是个dp啊。。。这几天出了好几道dp,我都没看出来,我竟然折磨菜。
考试的时候先打了个暴力,然后就开始往容斥上想。。。。
解析:
考虑dp。
令dp[i] 表示以i为结尾的,合法的子串数量。
令match[i] 表示进行括号匹配时,与i匹配的括号的编号。
(以上i都是右括号,如果是左括号置为0即可)
然后,就有: if(match[i]) dp[i]=dp[match[i]-1]+1;
这个转移方程的含义如下:
首先是前面的判断语句。必须是在i有匹配的情况下。
这样就排除了两种不可能的情况,一种是i是左括号,另一种是i是右括号,但在进行括号匹配时,没有与其匹配的左括号。
显然以上两种情况,i都不可能成为一个合法字串的结尾。
然后是要先给dp[i]加上1。这是以match[i]为起点,i为终点的子串的贡献。
其次要加上dp[match[i]-1];
这时分两种情况讨论。
第一种是 s[match[i]-1]==')' : 好丑的图
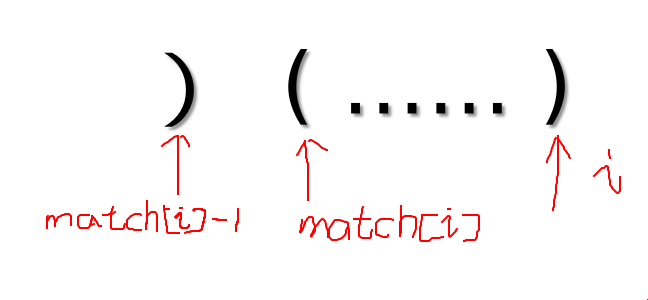
此时以i为结尾的子串还可能继续向左延伸,只要加上dp[match[i]-1]即可。
另外一种是 s[match[i]-1]=='(':

此时不能继续向左延伸,所以不加,但是因为dp[match[i]-1]是0,所以加上也不会错(主要是这样写起来方便)
说的有些麻烦了,其实还是挺显然的。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1000000+10;
#define gc() (p1 == p2 ? (p2 = buf + fread(p1 = buf, 1, 1 << 20, stdin), p1 == p2 ? EOF : *p1++) : *p1++)
#define read() ({ register int x = 0, f = 1; register char c = gc(); while(c < '0' || c > '9') { if (c == '-') f = -1; c = gc();} while(c >= '0' && c <= '9') x = x * 10 + (c & 15), c = gc(); f * x; })
char buf[1 << 20], *p1, *p2;
char s[maxn];
int n,top;
int dp[maxn];
int match[maxn];
ll ans;
struct node{
int pos;
char c;
node(){}
node(int x,char y){
pos=x;
c=y;
}
}Stack[maxn];
void Solve(){
scanf("%s",s+1);
n=strlen(s+1);
Stack[++top]=node(1,s[1]);
for(int i=2;i<=n;++i){
if(s[i]==')'&&Stack[top].c=='('){
node t=Stack[top];
top--;
match[i]=t.pos;
}else Stack[++top]=node(i,s[i]);
}
for(int i=1;i<=n;++i){
if(match[i]){
dp[i]=1+dp[match[i]-1];
}
}
for(int i=1;i<=n;++i) ans+=dp[i];
printf("%lld\n",ans);
}
int main(){
freopen("bracket.in","r",stdin);
freopen("bracket.out","w",stdout);
Solve();
return 0;
}
luogu P5658 [CSP/S 2019 D1T2] 括号树
前言:
其实应该不是很难吧。。。
解析:
和上一道题类似,但不是完全相同废话
所以一定要看清题啊。。。
这次问的是每个字符串的合法子串数量。。。我当成以每个字符结尾的合法字串数量了,直接暴毙。。。
会上面那道题,这个就简单多了。
先令dp[i]表示以i结尾的合法字子串数量,然后求个树上前缀和就行了。
照上个题的思路,改改式子:
if(match[i]) dp[i]=dp[fa[match[i]]]+1
最后。。。
不开long long见祖宗!
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=500000+10;
#define gc() (p1 == p2 ? (p2 = buf + fread(p1 = buf, 1, 1 << 20, stdin), p1 == p2 ? EOF : *p1++) : *p1++)
#define read() ({ register int x = 0, f = 1; register char c = gc(); while(c < '0' || c > '9') { if (c == '-') f = -1; c = gc();} while(c >= '0' && c <= '9') x = x * 10 + (c & 15), c = gc(); f * x; })
char buf[1 << 20], *p1, *p2;
struct node{
int to,nxt;
}edge[maxn<<1];
int head[maxn],fa[maxn],match[maxn];
ll dp[maxn];
char s[maxn];
struct Node{
int pos;
char c;
Node(){}
Node(int x,char y){
pos=x;
c=y;
}
}Stack[maxn];
int n,cnt,top;
ll ans;
void add(int from,int to){
edge[++cnt].to=to;
edge[cnt].nxt=head[from];
head[from]=cnt;
}
void dfs1(int u){
Node t=Stack[top];
if(t.c=='('&&s[u]==')'){
match[u]=t.pos;
top--;
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(v==fa[u]) continue;
dfs1(v);
}
Stack[++top]=Node(t.pos,t.c);
}else{
Stack[++top]=Node(u,s[u]);
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(v==fa[u]) continue;
dfs1(v);
}
top--;
}
}
void dfs2(int u){
if(match[u]) dp[u]=dp[fa[match[u]]]+1;
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(v==fa[u]) continue;
dfs2(v);
}
}
void dfs3(int u,int f){
dp[u]+=dp[f];
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(v==fa[u]) continue;
dfs3(v,u);
}
}
void Solve(){
scanf("%d%s",&n,s+1);
for(int i=2;i<=n;++i){
scanf("%d",&fa[i]);
add(i,fa[i]);
add(fa[i],i);
}
dfs1(1);
dfs2(1);
dfs3(1,0);
for(int i=1;i<=n;++i) ans^=(1ll*i*dp[i]);
printf("%lld\n",ans);
}
int main(){
// freopen("brackets.in","r",stdin);
// freopen("brackets.out","w",stdout);
Solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号