联赛膜你测试20 T1 Simple 题解 && NOIP2017 小凯的疑惑 题解（赛瓦维斯特定理）

前言：

数学题，对于我这种菜B还是需要多磨啊

Simple

首先它问不是好数的数量，可以转化为用总数量减去是好数的数量。
求“好数”的数量：
由裴蜀定理得，如果某个数\(i\)不能整除\(gcd(n,m)\),那么一定不是好数。
所以，我们把\(n,m,q\)分别除以\(gcd(n,m)\)，是不影响得出的“好数”数量的。
好，那么现在\(n,m\)就互质了。
现在，就把问题转化为了（用比较形象化的语言来说，就是）有\(n,m\)互质，求\([1,q]\)中有多少个数能被若干个\(n,m\)相加之后拼起来。
这个东西简单枚举两维的话，复杂度显然无法接受。我们可以考虑只枚举一维。
设\(n\)的系数是\(x\)，\(m\)的系数是\(y\)，且\(n\)小于\(m\)。
即\(n*x+m*y=c\);
那么就可以枚举\(y\)，求\(x\)的数量即可。
边界问题很重要。
我们考虑y的边界，因为要算\((c-m*y)/n\)，所以\(m*y<=c\);
然后会发现一个问题，如下图。

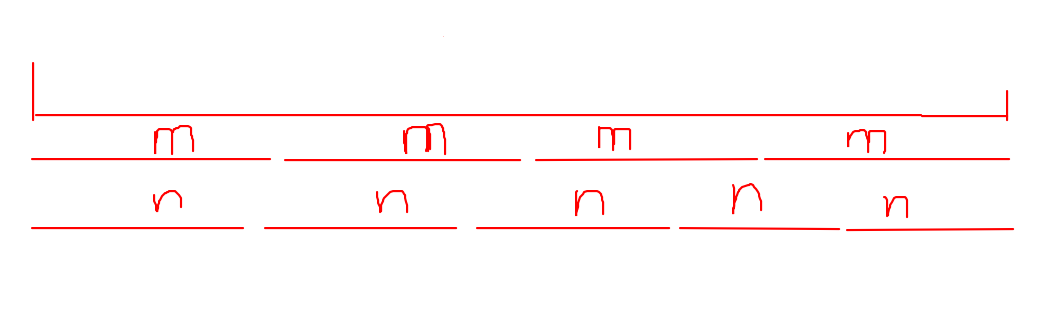
上面的长线段代表某个能被拼成的数，我们可以发现，如果枚举\(m\)的个数等于\(4\)时，这个数会被计算到。枚举\(m\)的个数等于\(0\),即\(n\)的个数等于\(5\)时，这个数又会被计算到，就会算重。
那么怎么去重呢？
我们会发现，因为\(n,m\)互质，上面的情况发生且只会发生在枚举的\(y\)大于等于\(n\)时才会出现。
所以就有了y的第二个边界，\(y<n\);
代码如下：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m,q;
ll gcd(ll x,ll y){
	return y==0 ? x : gcd(y,x%y) ;
}
void Solve(){
	int T;scanf("%d",&T);
	while(T--){
		scanf("%lld%lld%lld",&n,&m,&q);
		ll ans=q;
		if(n>m) swap(n,m);
		ll ss=gcd(n,m);
		n/=ss;
		m/=ss;
		q/=ss;
		for(register int i=0;i*m<=q&&i<n;++i) ans-=(q-1ll*i*m)/n+1;
		printf("%lld\n",ans+1);//ans+1的原因？
	}
}
int main(){
	freopen("simple.in","r",stdin);
	freopen("simple.out","w",stdout);
	Solve();
	return 0;
}

这里还要注意一个点，最后\(ans\)要加一，原因是\(x=0,y=0\)的情况，这是不在\([1,q]\)区间中的，相当于多减去一个，然后就要加回来。

2.luogu P3951 小凯的疑惑 / [蓝桥杯2013省]买不到的数目

链接

这个题放在D1T1是来恶心人的吗。。。找到规律就秒切，找不到规律就心态炸裂？
希望今年别出这种题。
据某工具人学长 所言，这玩意叫赛瓦维斯特定理。
emmm。。。动动的证明看懂了一部分
后来又看了这个链接疑似挂掉的博客
发现竟然折磨简单。
然后。。。我自己写的证明就先咕了吧