树链剖分好(du)题(liu)选做
1.luogu P4315 月下“毛景树”
前言:
这大概是本蒟蒻A掉的题里面码量最大的一道题了。我自认为码风比较紧凑,但还是写了175行。
从下午2点多调到晚上8点。中间小错不断。最后还是借助了郭神的AC代码。。
%%%stO郭神Orz%%%
还是我代码能力不够。以后要多写一些这样的题练练手。
解析:
题目相当裸。树链剖分+线段树维护区间最大值。
需要注意的点大致如下:
1.边权化点权
2.线段树需要实现的功能:区间加,区间赋值,区间查询最大值。
看起来貌似有手就行其实对于郭神这样的神犇确实有手就行,但是本蒟蒻调了一下午。。。
犯的其实都是一些低错,大概如下:
1.3个modify函数用串了
2.树链剖分跳top的时候,注意是 \(dfn[top[u]]<=dfn[u]\) ,因此应该是modifyfz(1,1,n,dfn[top[u]],dfn[u],w);
而不是modifyfz(1,1,n,dfn[u],dfn[top[u]],w);
3.注意在pushdown的时候要先判一下有没有区间赋值标记。
真正因为有理解上的问题而犯的错误:
在区间修改时要下传标记。每次更新前要保证该节点的状态一定是最新的,否则就会出错。
完整代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn=100000+10;
int dfn[maxn],head[maxn],top[maxn],size[maxn],fa[maxn],w[maxn],son[maxn],depth[maxn],tree[maxn<<2],lazyfz[maxn<<2],lazyadd[maxn<<2];
int n,cnt,Time;
struct node{
int to,next,val;
}edge[maxn<<1];
struct Node{
int from,to;
}b[maxn];
void add(int from,int to,int val){
edge[++cnt].to=to;
edge[cnt].val=val;
edge[cnt].next=head[from];
head[from]=cnt;
}
void dfs1(int u,int f){
fa[u]=f;
size[u]=1;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==f) continue;
depth[v]=depth[u]+1;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
void dfs2(int u,int t,int s){
top[u]=t;
dfn[u]=++Time;
w[Time]=s;
if(son[u]){
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==son[u]){
dfs2(v,t,edge[i].val);
break;
}
}
}
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v,edge[i].val);
}
}
void build(int rt,int l,int r){
lazyfz[rt]=-1;
if(l==r){
tree[rt]=w[l];
return;
}
int mid=(l+r)>>1;
build(rt<<1,l,mid);
build(rt<<1|1,mid+1,r);
tree[rt]=max(tree[rt<<1],tree[rt<<1|1]);
}
void updateadd(int rt,int w){
tree[rt]+=w;
lazyadd[rt]+=w;
}
void updatefz(int rt,int w){
tree[rt]=lazyfz[rt]=w;
lazyadd[rt]=0;
}
void pushdown(int rt){
if(lazyfz[rt]!=-1){
updatefz(rt<<1,lazyfz[rt]);
updatefz(rt<<1|1,lazyfz[rt]);
lazyfz[rt]=-1;
}
if(lazyadd[rt]){
updateadd(rt<<1,lazyadd[rt]);
updateadd(rt<<1|1,lazyadd[rt]);
lazyadd[rt]=0;
}
}
void modifyfz(int rt,int l,int r,int s,int t,int w){
if(s<=l&&r<=t){
updatefz(rt,w);
return;
}
int mid=(l+r)>>1;
pushdown(rt);
if(s<=mid) modifyfz(rt<<1,l,mid,s,t,w);
if(t>mid) modifyfz(rt<<1|1,mid+1,r,s,t,w);
tree[rt]=max(tree[rt<<1],tree[rt<<1|1]);
}
void Cover(int u,int v,int w){
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
modifyfz(1,1,n,dfn[top[u]],dfn[u],w);
u=fa[top[u]];
}
if(v==u) return;
if(depth[u]>depth[v]) swap(u,v);
modifyfz(1,1,n,dfn[u]+1,dfn[v],w);
}
void modifyadd(int rt,int l,int r,int s,int t,int w){
if(s<=l&&r<=t){
updateadd(rt,w);
return;
}
int mid=(l+r)>>1;
pushdown(rt);
if(s<=mid) modifyadd(rt<<1,l,mid,s,t,w);
if(t>mid) modifyadd(rt<<1|1,mid+1,r,s,t,w);
tree[rt]=max(tree[rt<<1],tree[rt<<1|1]);
}
void Modify(int u,int v,int w){
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
modifyadd(1,1,n,dfn[top[u]],dfn[u],w);
u=fa[top[u]];
}
if(u==v) return;
if(depth[u]>depth[v]) swap(u,v);
modifyadd(1,1,n,dfn[u]+1,dfn[v],w);
}
int query(int rt,int l,int r,int s,int t){
if(s<=l&&r<=t) return tree[rt];
int mid=(l+r)>>1;
pushdown(rt);
if(t<=mid) return query(rt<<1,l,mid,s,t);
if(s>mid) return query(rt<<1|1,mid+1,r,s,t);
return max(query(rt<<1,l,mid,s,t),query(rt<<1|1,mid+1,r,s,t));
}
int Query(int u,int v){
int res=-1e9;
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
res=max(res,query(1,1,n,dfn[top[u]],dfn[u]));
u=fa[top[u]];
}
if(u==v) return res;
if(depth[u]>depth[v]) swap(u,v);
res=max(res,query(1,1,n,dfn[u]+1,dfn[v]));
return res;
}
void Solve(){
scanf("%d",&n);
for(int i=1,z;i<n;++i){
scanf("%d%d%d",&b[i].from,&b[i].to,&z);
add(b[i].from,b[i].to,z);
add(b[i].to,b[i].from,z);
}
dfs1(1,0);
dfs2(1,1,0);
build(1,1,n);
char ccc[10];
int x,y,z;
for(;;){
scanf("%s",ccc);
if(ccc[0]=='S') return;
if(ccc[1]=='h'){
scanf("%d%d",&x,&y);
int d=max(dfn[b[x].from],dfn[b[x].to]);
modifyfz(1,1,n,d,d,y);
}else if(ccc[1]=='o'){
scanf("%d%d%d",&x,&y,&z);
Cover(x,y,z);
}else if(ccc[1]=='d'){
scanf("%d%d%d",&x,&y,&z);
Modify(x,y,z);
}else{
scanf("%d%d",&x,&y);
printf("%d\n",Query(x,y));
}
}
}
int main(){
Solve();
return 0;
}
2.luogu P1505 [国家集训队]旅游
前言:
又是一道毒瘤题。代码201行。不过有了上一道题的经验之后就好解决多了。然而调试还是花了将近2小时
解析:
其实还是一道裸题。
这次线段树的功能有:区间变相反数,区间查询最大、最小值,区间求和,单点赋值。
需要注意的点:
1.因为有区间变相反数,因此pushdown时需要把最大值变成原来最小值的相反数,最小值同理。
然后我就把pushdown写成了这样:
void update(int rt){
treesum[rt]*=-1;
treemax[rt]=treemin[rt]*(-1);
treemin[rt]=treemax[rt]*(-1);
lazy[rt]*=-1;
}
void pushdown(int rt){
if(lazy[rt]==1) return;
update(rt<<1);
update(rt<<1|1);
lazy[rt]=1;
}
然后就挂了。
所以其实就是交换两个整数,显然不能直接换,所以要加一个中间变量
然后就写成这样:
void update(int rt){
treesum[rt]*=-1;
int x=treemax[rt];
treemax[rt]=treemin[rt]*(-1);
treemin[rt]=x*(-1);
lazy[rt]*=-1;
}
具体在调试过程中,还有一个理解上的问题。
int querysum(int rt,int l,int r,int s,int t){
if(s<=l&&r<=t){
//这里是不需要pushdown的。
return treesum[rt];
}
int mid=(l+r)>>1;
pushdown(rt);
if(t<=mid) return querysum(rt<<1,l,mid,s,t);
if(s>mid) return querysum(rt<<1|1,mid+1,r,s,t);
return querysum(rt<<1,l,mid,s,t)+querysum(rt<<1|1,mid+1,r,s,t);
}
因为除了我全世界都知道,线段树的lazy标记是用来标记该节点的子节点的,跟这个节点本身没有关系。
完整代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn=2e5+10;
struct node{
int to,next,val;
}edge[maxn<<1];
int lazy[maxn<<2],treesum[maxn<<2],a[maxn],w[maxn],treemax[maxn<<2],treemin[maxn<<2],size[maxn],top[maxn],son[maxn],depth[maxn],fa[maxn],head[maxn],dfn[maxn];
struct Node{
int from,to;
}b[maxn];
int n,m,x,y,z,o,Time,cnt;
char ccc[7];
void add(int from,int to,int val){
edge[++cnt].to=to;
edge[cnt].val=val;
edge[cnt].next=head[from];
head[from]=cnt;
}
void pushup(int rt){
treesum[rt]=treesum[rt<<1]+treesum[rt<<1|1];
treemax[rt]=max(treemax[rt<<1],treemax[rt<<1|1]);
treemin[rt]=min(treemin[rt<<1],treemin[rt<<1|1]);
}
void build(int rt,int l,int r){
lazy[rt]=1;
if(l==r){
treesum[rt]=treemax[rt]=treemin[rt]=w[l];
return;
}
int mid=(l+r)>>1;
build(rt<<1,l,mid);
build(rt<<1|1,mid+1,r);
pushup(rt);
}
void dfs1(int u,int f){
fa[u]=f;
size[u]=1;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==f) continue;
depth[v]=depth[u]+1;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
void dfs2(int u,int t,int s){
top[u]=t;
dfn[u]=++Time;
w[Time]=s;
if(son[u]){
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==son[u]){
dfs2(v,t,edge[i].val);
break;
}
}
}
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v,edge[i].val);
}
}
void update(int rt){
treesum[rt]*=-1;
int x=treemax[rt];
treemax[rt]=treemin[rt]*(-1);
treemin[rt]=x*(-1);
lazy[rt]*=-1;
}
void pushdown(int rt){
if(lazy[rt]==1) return;
update(rt<<1);
update(rt<<1|1);
lazy[rt]=1;
}
void modify(int rt,int l,int r,int x,int k){
if(l==r){
treesum[rt]=treemax[rt]=treemin[rt]=k;
lazy[rt]=1;
return;
}
int mid=(l+r)>>1;
pushdown(rt);
if(x<=mid) modify(rt<<1,l,mid,x,k);
else modify(rt<<1|1,mid+1,r,x,k);
pushup(rt);
}
void modify2(int rt,int l,int r,int s,int t){
if(s<=l&&r<=t){
update(rt);
return;
}
pushdown(rt);
int mid=(l+r)>>1;
if(s<=mid) modify2(rt<<1,l,mid,s,t);
if(t>mid) modify2(rt<<1|1,mid+1,r,s,t);
pushup(rt);
}
void Modify(int u,int v){
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
modify2(1,1,n,dfn[top[u]],dfn[u]);
u=fa[top[u]];
}
if(u==v) return;
if(depth[u]>depth[v]) swap(u,v);
modify2(1,1,n,dfn[u]+1,dfn[v]);
}
int querymax(int rt,int l,int r,int s,int t){
if(s<=l&&r<=t) return treemax[rt];
int mid=(l+r)>>1;
pushdown(rt);
if(t<=mid) return querymax(rt<<1,l,mid,s,t);
if(s>mid) return querymax(rt<<1|1,mid+1,r,s,t);
return max(querymax(rt<<1,l,mid,s,t),querymax(rt<<1|1,mid+1,r,s,t));
}
int Querymax(int u,int v){
int res=-1e9;
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
res=max(res,querymax(1,1,n,dfn[top[u]],dfn[u]));
u=fa[top[u]];
}
if(u==v) return res;
if(depth[u]>depth[v]) swap(u,v);
res=max(res,querymax(1,1,n,dfn[u]+1,dfn[v]));
return res;
}
int querymin(int rt,int l,int r,int s,int t){
if(s<=l&&r<=t) return treemin[rt];
int mid=(l+r)>>1;
pushdown(rt);
if(t<=mid) return querymin(rt<<1,l,mid,s,t);
if(s>mid) return querymin(rt<<1|1,mid+1,r,s,t);
return min(querymin(rt<<1,l,mid,s,t),querymin(rt<<1|1,mid+1,r,s,t));
}
int Querymin(int u,int v){
int res=0x7fffffff;
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
res=min(res,querymin(1,1,n,dfn[top[u]],dfn[u]));
u=fa[top[u]];
}
if(u==v) return res;
if(depth[u]>depth[v]) swap(u,v);
res=min(res,querymin(1,1,n,dfn[u]+1,dfn[v]));
return res;
}
int querysum(int rt,int l,int r,int s,int t){
if(s<=l&&r<=t) return treesum[rt];
int mid=(l+r)>>1;
pushdown(rt);
if(t<=mid) return querysum(rt<<1,l,mid,s,t);
if(s>mid) return querysum(rt<<1|1,mid+1,r,s,t);
return querysum(rt<<1,l,mid,s,t)+querysum(rt<<1|1,mid+1,r,s,t);
}
int Querysum(int u,int v){
int res=0;
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
res+=querysum(1,1,n,dfn[top[u]],dfn[u]);
u=fa[top[u]];
}
if(u==v) return res;
if(depth[u]>depth[v]) swap(u,v);
res+=querysum(1,1,n,dfn[u]+1,dfn[v]);
return res;
}
void Solve(){
scanf("%d",&n);
for(int i=1;i<n;++i){
scanf("%d%d%d",&b[i].from,&b[i].to,&z);
b[i].from++;
b[i].to++;
add(b[i].from,b[i].to,z);
add(b[i].to,b[i].from,z);
}
dfs1(1,0);
dfs2(1,1,0);
build(1,1,n);
scanf("%d",&m);
for(int i=1;i<=m;++i){
scanf("%s%d%d",ccc,&x,&y);
if(ccc[0]=='C'){
o=max(dfn[b[x].from],dfn[b[x].to]);
modify(1,1,n,o,y);
}
x++;
y++;
if(ccc[0]=='N') Modify(x,y);
else if(ccc[0]=='S') printf("%d\n",Querysum(x,y));
else if(ccc[1]=='A') printf("%d\n",Querymax(x,y));
else if(ccc[1]=='I') printf("%d\n",Querymin(x,y));
}
}
int main(){
Solve();
return 0;
}
3.luogu P2146 [NOI2015]软件包管理器
前言:
这道题其实并不难,码量也就100行。不过我刚开始做的时候把问题想复杂了,有一些点没想清楚,就导致写了很长时间。因为码量较小,其实调试时间并不长。
解析:
其实还是一道裸题。
可以发现安装一个包就是把这个点到根节点的路径里所有的点都变成1,卸载一个包就是把这个点的子树里面所有的点都变成0。
其实树剖维护子树的题好像挺少的,我目前只见过这个题和P3384 【模板】轻重链剖分 里面涉及到这个操作。可能是因为这个太简单了。因为一棵子树中的dfs序是连续的,所以很好处理。
但是sbwzx在刚开始的时候竟然没想到。。。因为脑子比较混乱,就错误地把卸载一个包当成把这个点和根节点里面所有的点都变成0了,然后惊喜地发现连样例都过不去。
最后还是看了一眼题解才想明白,wtcl。这种sb错误全世界应该只有我一个人犯了吧。
这次线段树的功能有:区间赋值,查询区间和。
需要注意的点:貌似没啥,挺好写的
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=100000+10;
int head[maxn],tree[maxn<<2],top[maxn],depth[maxn],size[maxn],dfn[maxn],fa[maxn],son[maxn],lazy[maxn<<2];
int n,cnt,Time,q;
struct node{
int to,next;
}edge[maxn<<1];
ll ans;
void add(int from,int to){
edge[++cnt].to=to;
edge[cnt].next=head[from];
head[from]=cnt;
}
void dfs1(int u){
size[u]=1;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==fa[u]) continue;
depth[v]=depth[u]+1;
dfs1(v);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
void dfs2(int u,int t){
top[u]=t;
dfn[u]=++Time;
if(son[u]) dfs2(son[u],t);
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
void update(int rt,int l,int r,int w){
lazy[rt]=w;
tree[rt]=w*(r-l+1);
}
void pushdown(int rt,int l,int r){
if(lazy[rt]!=-1){
int mid=(l+r)>>1;
update(rt<<1,l,mid,lazy[rt]);
update(rt<<1|1,mid+1,r,lazy[rt]);
lazy[rt]=-1;
}
}
void modify(int rt,int l,int r,int s,int t,int w){
if(s<=l&&r<=t){
update(rt,l,r,w);
return;
}
int mid=(l+r)>>1;
pushdown(rt,l,r);
if(s<=mid) modify(rt<<1,l,mid,s,t,w);
if(t>mid) modify(rt<<1|1,mid+1,r,s,t,w);
tree[rt]=tree[rt<<1]+tree[rt<<1|1];
}
int query(int rt,int l,int r,int s,int t){
if(s<=l&&r<=t) return tree[rt];
int mid=(l+r)>>1;
pushdown(rt,l,r);
if(t<=mid) return query(rt<<1,l,mid,s,t);
if(s>mid) return query(rt<<1|1,mid+1,r,s,t);
return query(rt<<1,l,mid,s,t)+query(rt<<1|1,mid+1,r,s,t);
}
int Query0(int y){
int res=query(1,1,n,dfn[y],dfn[y]+size[y]-1);
modify(1,1,n,dfn[y],dfn[y]+size[y]-1,0);
return res;
}
int Query1(int y){
int res=0;
while(top[y]!=1){
res+=dfn[y]-dfn[top[y]]+1-query(1,1,n,dfn[top[y]],dfn[y]);
modify(1,1,n,dfn[top[y]],dfn[y],1);
y=fa[top[y]];
}
res+=dfn[y]-query(1,1,n,1,dfn[y]);
modify(1,1,n,1,dfn[y],1);
return res;
}
void Solve(){
scanf("%d",&n);
for(int i=2;i<=n;++i){
scanf("%d",&fa[i]);
fa[i]++;
add(i,fa[i]);
add(fa[i],i);
}
dfs1(1);
dfs2(1,1);
memset(lazy,-1,sizeof(lazy));
scanf("%d",&q);
char ccc[20];
for(int i=1,x;i<=q;++i){
scanf("%s%d",ccc,&x);
x++;
if(ccc[0]=='i') printf("%d\n",Query1(x));
else printf("%d\n",Query0(x));
}
}
int main(){
Solve();
return 0;
}
4.luogu P4281 [AHOI2008]紧急集合 / 聚会
前言:
这题就带一点思维了。我第一眼做的时候以为是个码力题,对题目最关键的性质并没有看清楚,最后看了题解才明白。思维力太差,自己做题的时候都不愿意去想太多,可能是我最近做不用脑子的题太多了,要好好反思一下。
解析:
首先一眼看去,前置知识显然只有树剖求Lca,关键就是怎么用到这个题里面。
因为是三个点,所以对我来说并不是很显然的样子。
我们的目标是找到树上某一点,使这个点到树上某三个点的距离之和最小。
两个点的话,显然是Lca,那么三个点呢?
首先我想到的是三个点的Lca,但是等我写出来之后连样例都过不了。
后来我一看,这显然是错的啊,即使是这样我也还是傻傻地写了出来
考虑三个点如果在同一条链上,那么最后答案一定是中间的那个点,那显然不是Lca。
当我想到这里的时候人就傻了,然后就直接去看题解。看完结论才发现如果自己好好想想应该也能想出来,唉。
结论:这个点是三个两两之间的Lca中,深度最大的那个点。
证明:其实想到这个以后就挺显然了
我们把要求的三个点称为\(u,v,w\) ,正确答案称为\(x\);
1.假设三个点在同一条链上,显然正确。
2.假设其中一个点(不妨设为w)与另外两点(不妨设为u,v)不在一条链上。
(设u是v的祖先)
假设w的深度小于v,那么答案就是Lca(w,v);
假设w的深度大于v,那么不妨交换w,v,Lca(w,v)不变,还是对的
(写的有点绕?其实感觉只要想到这个性质,后面证明就挺显然的)
代码就相当好写了,写完后甚至不用调一遍AC:
#include <bits/stdc++.h>
using namespace std;
const int maxn=500000+10;
struct node{
int to,next;
}edge[maxn<<1];
int head[maxn],top[maxn],size[maxn],son[maxn],fa[maxn],depth[maxn];
int n,m,cnt,ans;
void add(int from,int to){
edge[++cnt].to=to;
edge[cnt].next=head[from];
head[from]=cnt;
}
void dfs1(int u,int f){
size[u]=1;
fa[u]=f;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==f) continue;
depth[v]=depth[u]+1;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
void dfs2(int u,int t){
top[u]=t;
if(son[u]) dfs2(son[u],t);
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
int Lca(int u,int v){
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
u=fa[top[u]];
}
return depth[u]<depth[v] ? u : v ;
}
int query(int u,int v){
int res=0;
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
res+=depth[u]-depth[top[u]]+1;
u=fa[top[u]];
}
res+=abs(depth[u]-depth[v]);
return res;
}
int Query(int u,int v,int w){
ans=0;
int l1=Lca(u,v);
int x=l1;
int l2=Lca(u,w);
x=depth[x] > depth[l2] ? x : l2 ;
int l3=Lca(v,w);
x=depth[x] > depth[l3] ? x : l3 ;
ans+=query(u,x);
ans+=query(v,x);
ans+=query(w,x);
return x;
}
void Solve(){
scanf("%d%d",&n,&m);
for(int i=1,x,y;i<n;++i){
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
dfs1(1,0);
dfs2(1,1);
for(int i=1,x,y,z;i<=m;++i){
scanf("%d%d%d",&x,&y,&z);
int tool=Query(x,y,z);
printf("%d %d\n",tool,ans);
}
}
int main(){
Solve();
return 0;
}
5.luogu P2486 [SDOI2011]染色
前言:
第一次想做这道题还是在小集训的时候,我刚开始学树剖。当时觉得不是很好维护于是就弃了。最近又拿出来,感觉并不难。这道题分了很多时间段写,总体的解决时间很短,也算是一个进步吧。
解析:
主要问题在线段树上。因为要维护的是区间连续段的个数,所以不是很板子。
想一下应该还是比较好实现的。
线段树维护区间连续段的个数,再记录赋值标记。
因为要方便合并,所以还要维护这个区间最左边和最右边的颜色编号是多少。
然后好像就没了,注意细节吧。
代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn=500000+10;
struct node{
int to,next;
}edge[maxn<<1];
int head[maxn],top[maxn],size[maxn],son[maxn],fa[maxn],depth[maxn],dfn[maxn],a[maxn],w[maxn];
int n,m,cnt,Time;
struct Segment_tree{
int val,lazy,lc,rc;//lc,rc分别表示这个区间左右端点的color,lazy==-1时表示没有赋值
}tree[maxn<<2];
void add(int from,int to){
edge[++cnt].to=to;
edge[cnt].next=head[from];
head[from]=cnt;
}
void dfs1(int u,int f){
size[u]=1;
fa[u]=f;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==f) continue;
depth[v]=depth[u]+1;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
void dfs2(int u,int t){
top[u]=t;
dfn[u]=++Time;
w[Time]=a[u];
if(son[u]) dfs2(son[u],t);
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
void pushup(int rt){
tree[rt].lc=tree[rt<<1].lc;
tree[rt].rc=tree[rt<<1|1].rc;
tree[rt].val=tree[rt<<1].val+tree[rt<<1|1].val;
if(tree[rt<<1].rc==tree[rt<<1|1].lc) tree[rt].val--;
}
void update(int rt,int x){
tree[rt].lazy=x;
tree[rt].val=1;
tree[rt].lc=tree[rt].rc=x;
}
void pushdown(int rt){
if(tree[rt].lazy==-1) return;
tree[rt].val=1;
update(rt<<1,tree[rt].lazy);
update(rt<<1|1,tree[rt].lazy);
tree[rt].lazy=-1;
}
void modify(int rt,int l,int r,int s,int t,int p){
if(s<=l&&r<=t){
update(rt,p);
return;
}
int mid=(l+r)>>1;
pushdown(rt);
if(s<=mid) modify(rt<<1,l,mid,s,t,p);
if(t>mid) modify(rt<<1|1,mid+1,r,s,t,p);
pushup(rt);
}
void build(int rt,int l,int r){
tree[rt].lazy=-1;
if(l==r){
tree[rt].val=1;
tree[rt].lc=tree[rt].rc=w[l];
return;
}
int mid=(l+r)>>1;
build(rt<<1,l,mid);
build(rt<<1|1,mid+1,r);
pushup(rt);
}
int query2(int rt,int l,int r,int x){
if(l==r) return tree[rt].lc;
int mid=(l+r)>>1;
pushdown(rt);
if(x<=mid) return query2(rt<<1,l,mid,x);
else return query2(rt<<1|1,mid+1,r,x);
}
int query(int rt,int l,int r,int s,int t){
if(s<=l&&r<=t) return tree[rt].val;
int mid=(l+r)>>1;
pushdown(rt);
if(t<=mid) return query(rt<<1,l,mid,s,t);
if(s>mid) return query(rt<<1|1,mid+1,r,s,t);
return query(rt<<1,l,mid,s,t)+query(rt<<1|1,mid+1,r,s,t)-(tree[rt<<1].rc==tree[rt<<1|1].lc);
}
int Query(int u,int v){
int res=0;
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
res+=query(1,1,n,dfn[top[u]],dfn[u]);
if(top[u]!=1 && query2(1,1,n,dfn[top[u]])==query2(1,1,n,dfn[fa[top[u]]])) res--;
u=fa[top[u]];
}
if(depth[u]>depth[v]) swap(u,v);
res+=query(1,1,n,dfn[u],dfn[v]);
return res;
}
void Modify(int u,int v,int x){
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
modify(1,1,n,dfn[top[u]],dfn[u],x);
u=fa[top[u]];
}
if(depth[u]>depth[v]) swap(u,v);
modify(1,1,n,dfn[u],dfn[v],x);
}
void Solve(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
for(int i=1,x,y;i<n;++i){
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
dfs1(1,0);
dfs2(1,1);
build(1,1,n);
char ccc[5];
for(int i=1,x,y,z;i<=m;++i){
scanf("%s%d%d",ccc,&x,&y);
if(ccc[0]=='Q') printf("%d\n",Query(x,y));
else{
scanf("%d",&z);
Modify(x,y,z);
}
}
}
int main(){
Solve();
return 0;
}
update 强烈谴责skyh题表里面的树链剖分难度!太水了! by 2020.10.12
S(A)kyh在luogu里面放了个数据结构题表,于是我去刷了一下里面的树剖题。
@skyh
6.luogu P4114 Qtree1
前言:
太水了没啥可说的,直接切了
解析:
无
代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn=100000+10;
int dfn[maxn],head[maxn],top[maxn],size[maxn],fa[maxn],son[maxn],depth[maxn],tree[maxn<<2],w[maxn];
struct node{
int to,next,val;
}edge[maxn<<1];
struct Node{
int from,to;
}b[maxn];
int cnt,n,Time;
void add(int from,int to,int val){
edge[++cnt].to=to;
edge[cnt].val=val;
edge[cnt].next=head[from];
head[from]=cnt;
}
void dfs1(int u,int f){
size[u]=1;
fa[u]=f;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==f) continue;
depth[v]=depth[u]+1;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
void dfs2(int u,int t,int s){
top[u]=t;
dfn[u]=++Time;
w[Time]=s;
if(son[u]){
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==son[u]){
dfs2(v,t,edge[i].val);
break;
}
}
}
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v,edge[i].val);
}
}
void build(int rt,int l,int r){
if(l==r){
tree[rt]=w[l];
return;
}
int mid=(l+r)>>1;
build(rt<<1,l,mid);
build(rt<<1|1,mid+1,r);
tree[rt]=max(tree[rt<<1],tree[rt<<1|1]);
}
int query(int rt,int l,int r,int s,int t){
if(s<=l&&r<=t) return tree[rt];
int mid=(l+r)>>1;
if(t<=mid) return query(rt<<1,l,mid,s,t);
if(s>mid) return query(rt<<1|1,mid+1,r,s,t);
return max(query(rt<<1,l,mid,s,t),query(rt<<1|1,mid+1,r,s,t));
}
int Query(int u,int v){
if(u==v) return 0;
int res=-0x3f3f3f3f;
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
res=max(res,query(1,1,n,dfn[top[u]],dfn[u]));
u=fa[top[u]];
}
if(u==v) return res;
if(depth[u]>depth[v]) swap(u,v);
res=max(res,query(1,1,n,dfn[u]+1,dfn[v]));
return res;
}
void modify(int rt,int l,int r,int x,int p){
if(l==r){
tree[rt]=p;
return;
}
int mid=(l+r)>>1;
if(x<=mid) modify(rt<<1,l,mid,x,p);
else modify(rt<<1|1,mid+1,r,x,p);
tree[rt]=max(tree[rt<<1],tree[rt<<1|1]);
}
void Solve(){
scanf("%d",&n);
for(int i=1,z;i<n;++i){
scanf("%d%d%d",&b[i].from,&b[i].to,&z);
add(b[i].from,b[i].to,z);
add(b[i].to,b[i].from,z);
}
dfs1(1,0);
dfs2(1,1,0);
build(1,1,n);
char ccc[10];
int x,y;
while(1){
scanf("%s",ccc);
if(ccc[0]=='D') return;
scanf("%d%d",&x,&y);
if(ccc[0]=='C'){
int s=max(dfn[b[x].from],dfn[b[x].to]);
modify(1,1,n,s,y);
}else printf("%d\n",Query(x,y));
}
}
int main(){
Solve();
return 0;
}
6.luogu P3833 [SHOI2012]魔法树
前言:
这个就更水了
解析:
无
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=100000+10;
struct Segment_tree{
ll val,lazy;
}tree[maxn<<2];
int head[maxn],dfn[maxn],fa[maxn],size[maxn],son[maxn],depth[maxn],top[maxn];
struct node{
int to,next;
}edge[maxn<<1];
int n,cnt,q,Time;
void add(int from,int to){
edge[++cnt].to=to;
edge[cnt].next=head[from];
head[from]=cnt;
}
void dfs1(int u){
size[u]=1;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==fa[u]) continue;
depth[v]=depth[u]+1;
dfs1(v);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
void dfs2(int u,int t){
top[u]=t;
dfn[u]=++Time;
if(son[u]) dfs2(son[u],t);
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
void update(int rt,int l,int r,int d){
tree[rt].val+=1ll*d*(r-l+1);
tree[rt].lazy+=d;
}
void pushdown(int rt,int l,int r){
if(tree[rt].lazy==0) return;
int mid=(l+r)>>1;
update(rt<<1,l,mid,tree[rt].lazy);
update(rt<<1|1,mid+1,r,tree[rt].lazy);
tree[rt].lazy=0;
}
void modify(int rt,int l,int r,int s,int t,int d){
if(s<=l&&r<=t){
update(rt,l,r,d);
return;
}
int mid=(l+r)>>1;
pushdown(rt,l,r);
if(s<=mid) modify(rt<<1,l,mid,s,t,d);
if(t>mid) modify(rt<<1|1,mid+1,r,s,t,d);
tree[rt].val=tree[rt<<1].val+tree[rt<<1|1].val;
}
void Modify(int u,int v,int d){
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
modify(1,1,n,dfn[top[u]],dfn[u],d);
u=fa[top[u]];
}
if(depth[u]>depth[v]) swap(u,v);
modify(1,1,n,dfn[u],dfn[v],d);
}
ll query(int rt,int l,int r,int s,int t){
if(s<=l&&r<=t) return tree[rt].val;
int mid=(l+r)>>1;
pushdown(rt,l,r);
if(t<=mid) return query(rt<<1,l,mid,s,t);
if(s>mid) return query(rt<<1|1,mid+1,r,s,t);
return query(rt<<1,l,mid,s,t)+query(rt<<1|1,mid+1,r,s,t);
}
void Solve(){
scanf("%d",&n);
for(int i=1,x,y;i<n;++i){
scanf("%d%d",&x,&y);
x++;
y++;
add(x,y);
add(y,x);
fa[y]=x;
}
dfs1(1);
dfs2(1,1);
scanf("%d",&q);
char ccc[5];
for(int i=1,u,v,d;i<=q;++i){
scanf("%s%d",ccc,&u);
u++;
if(ccc[0]=='A'){
scanf("%d%d",&v,&d);
v++;
Modify(u,v,d);
}
else printf("%lld\n",query(1,1,n,dfn[u],dfn[u]+size[u]-1));
}
}
int main(){
Solve();
return 0;
}
7.luogu P4427 [BJOI2018]求和
前言:
因为最近考试经常被爆踩,心情不爽就多写了两道树剖。像这种简单题大概能做到写代码不超过25分钟,调试不超过10分钟。虽然不是很快,不过也算可以了。
解析:
这个题不是很板子。不过一看k的范围就知道可以随便搞了。开50颗线段树,分别维护k次方和。然后普通的线段树求区间和即可。
代码:(好像跑的巨tm慢。。。)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=300000+10,mod=998244353;
struct node{
int to,next;
}edge[maxn<<1];
int head[maxn],size[maxn],fa[maxn],depth[maxn],top[maxn],dfn[maxn],son[maxn],w[maxn];
int n,cnt,Time,m;
ll tree[maxn<<2][60];
void add(int from,int to){
edge[++cnt].to=to;
edge[cnt].next=head[from];
head[from]=cnt;
}
void dfs1(int u,int f){
fa[u]=f;
size[u]=1;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==f) continue;
depth[v]=depth[u]+1;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
void dfs2(int u,int t){
top[u]=t;
dfn[u]=++Time;
w[Time]=depth[u];
if(son[u]) dfs2(son[u],t);
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
void pushup(int rt){
for(int i=1;i<=50;++i) tree[rt][i]=(tree[rt<<1][i]+tree[rt<<1|1][i])%mod;
}
void build(int rt,int l,int r){
if(l==r){
tree[rt][1]=w[l];
for(int i=2;i<=50;++i) tree[rt][i]=tree[rt][i-1]*w[l]%mod;
return;
}
int mid=(l+r)>>1;
build(rt<<1,l,mid);
build(rt<<1|1,mid+1,r);
pushup(rt);
}
ll query(int rt,int l,int r,int s,int t,int k){
if(s<=l&&r<=t) return tree[rt][k];
int mid=(l+r)>>1;
if(t<=mid) return query(rt<<1,l,mid,s,t,k);
if(s>mid) return query(rt<<1|1,mid+1,r,s,t,k);
return (query(rt<<1,l,mid,s,t,k)+query(rt<<1|1,mid+1,r,s,t,k))%mod;
}
ll Query(int u,int v,int k){
ll res=0;
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
res+=query(1,1,n,dfn[top[u]],dfn[u],k);
if(res>=mod) res-=mod;
u=fa[top[u]];
}
if(depth[u]>depth[v]) swap(u,v);
res+=query(1,1,n,dfn[u],dfn[v],k);
if(res>=mod) res-=mod;
return res;
}
void Solve(){
scanf("%d",&n);
for(int i=1,x,y;i<n;++i){
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
dfs1(1,0);
dfs2(1,1);
build(1,1,n);
scanf("%d",&m);
for(int i=1,x,y,z;i<=m;++i){
scanf("%d%d%d",&x,&y,&z);
printf("%lld\n",Query(x,y,z));
}
}
int main(){
Solve();
return 0;
}
8.luogu P4092 [HEOI2016/TJOI2016]树
前言:
这个是用线段树上二分维护。也不是很板子,不过也很好写。
解析:
线段树上二分。大概思路就是先查右区间,如果右区间查不到,就查左区间。我感觉有点不对劲的地方就是查询的复杂度。。。不过貌似跑的挺快。
代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn=100000+10;
int tree[maxn<<2],head[maxn],dfn[maxn],dfn_l[maxn],top[maxn],son[maxn],fa[maxn],depth[maxn],size[maxn];
int n,q,cnt,Time;
struct node{
int to,next;
}edge[maxn<<1];
void add(int from,int to){
edge[++cnt].to=to;
edge[cnt].next=head[from];
head[from]=cnt;
}
void dfs1(int u,int f){
size[u]=1;
fa[u]=f;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==f) continue;
depth[v]=depth[u]+1;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
void dfs2(int u,int t){
top[u]=t;
dfn[u]=++Time;
dfn_l[Time]=u;
if(son[u]) dfs2(son[u],t);
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
void modify(int rt,int l,int r,int pos){
if(l==r){
tree[rt]=1;
return;
}
int mid=(l+r)>>1;
if(pos<=mid) modify(rt<<1,l,mid,pos);
else modify(rt<<1|1,mid+1,r,pos);
tree[rt]=tree[rt<<1]+tree[rt<<1|1];
}
int query(int rt,int l,int r,int s,int t){
if(tree[rt]==0) return 0;
if(l==r) return l;
int mid=(l+r)>>1;
int res=0;
if(t>mid) res=query(rt<<1|1,mid+1,r,s,t);
if(res) return res;
if(s<=mid) res=query(rt<<1,l,mid,s,t);
return res;
}
int Query(int u){
int res;
while(top[u]!=1){
res=query(1,1,n,dfn[top[u]],dfn[u]);
if(res!=0) return res;
u=fa[top[u]];
}
res=query(1,1,n,1,dfn[u]);
return res;
}
void Solve(){
scanf("%d%d",&n,&q);
for(int i=1,x,y;i<n;++i){
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
dfs1(1,0);
dfs2(1,1);
modify(1,1,n,1);
char ccc[10];
for(int i=1,x;i<=q;++i){
scanf("%s%d",ccc,&x);
if(ccc[0]=='C') modify(1,1,n,dfn[x]);
else printf("%d\n",dfn_l[Query(x)]);
}
}
int main(){
Solve();
return 0;
}
9.luogu P2420 让我们异或吧
前言:
大水题。某天晚上9点36,没事干了,就敲了一个。正好赶在9点46的时候A掉。不错不错。
解析:
无
#include <bits/stdc++.h>
using namespace std;
const int maxn=100000+10;
int head[maxn],dfn[maxn],top[maxn],size[maxn],fa[maxn],son[maxn],depth[maxn],w[maxn];
int tree[maxn<<2];
struct node{
int to,next,val;
}edge[maxn<<1];
int n,m,cnt,Time;
void add(int from,int to,int val){
edge[++cnt].to=to;
edge[cnt].val=val;
edge[cnt].next=head[from];
head[from]=cnt;
}
void dfs1(int u,int f){
size[u]=1;
fa[u]=f;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==f) continue;
depth[v]=depth[u]+1;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
void dfs2(int u,int t,int s){
top[u]=t;
dfn[u]=++Time;
w[Time]=s;
if(son[u]){
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==son[u]){
dfs2(v,t,edge[i].val);
break;
}
}
}
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v,edge[i].val);
}
}
void build(int rt,int l,int r){
if(l==r){
tree[rt]=w[l];
return;
}
int mid=(l+r)>>1;
build(rt<<1,l,mid);
build(rt<<1|1,mid+1,r);
tree[rt]=tree[rt<<1]^tree[rt<<1|1];
}
int query(int rt,int l,int r,int s,int t){
if(s<=l&&r<=t) return tree[rt];
int mid=(l+r)>>1;
if(t<=mid) return query(rt<<1,l,mid,s,t);
if(s>mid) return query(rt<<1|1,mid+1,r,s,t);
return query(rt<<1,l,mid,s,t)^query(rt<<1|1,mid+1,r,s,t);
}
int Query(int u,int v){
int res=0;
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
res^=query(1,1,n,dfn[top[u]],dfn[u]);
u=fa[top[u]];
}
if(u==v) return res;
if(depth[u]>depth[v]) swap(u,v);
res^=query(1,1,n,dfn[u]+1,dfn[v]);
return res;
}
void Solve(){
scanf("%d",&n);
for(int i=1,x,y,z;i<n;++i){
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,z);
}
dfs1(1,0);
dfs2(1,1,0);
build(1,1,n);
scanf("%d",&m);
for(int i=1,x,y;i<=m;++i){
scanf("%d%d",&x,&y);
printf("%d\n",Query(x,y));
}
}
int main(){
Solve();
return 0;
}
10.luogu P3038 [USACO11DEC]Grass Planting G
前言:
大水题。没想到我做这道题最大的限制是我的英语水平。犯了一些沙雕错误。没有上一道打的好。
解析:
无
#include <bits/stdc++.h>
using namespace std;
const int maxn=100000+10;
int top[maxn],depth[maxn],fa[maxn],son[maxn],head[maxn],size[maxn],dfn[maxn],w[maxn];
int cnt,n,m,Time;
struct node{
int to,next;
}edge[maxn<<1];
struct Segment_tree{
int val,lazy;
}tree[maxn<<2];
void add(int from,int to){
edge[++cnt].to=to;
edge[cnt].next=head[from];
head[from]=cnt;
}
void dfs1(int u,int f){
fa[u]=f;
size[u]=1;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==f) continue;
depth[v]=depth[u]+1;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
void dfs2(int u,int t){
top[u]=t;
dfn[u]=++Time;
if(son[u]) dfs2(son[u],t);
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
void update(int rt,int l,int r,int w){
tree[rt].lazy+=w;
tree[rt].val+=w*(r-l+1);
}
void pushdown(int rt,int l,int r){
if(tree[rt].lazy==0) return;
int mid=(l+r)>>1;
update(rt<<1,l,mid,tree[rt].lazy);
update(rt<<1|1,mid+1,r,tree[rt].lazy);
tree[rt].lazy=0;
}
void modify(int rt,int l,int r,int s,int t){
if(s<=l&&r<=t){
update(rt,l,r,1);
return;
}
int mid=(l+r)>>1;
pushdown(rt,l,r);
if(s<=mid) modify(rt<<1,l,mid,s,t);
if(t>mid) modify(rt<<1|1,mid+1,r,s,t);
tree[rt].val=tree[rt<<1].val+tree[rt<<1|1].val;
}
void Modify(int u,int v){
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
modify(1,1,n,dfn[top[u]],dfn[u]);
u=fa[top[u]];
}
if(u==v) return;
if(depth[u]>depth[v]) swap(u,v);
modify(1,1,n,dfn[u]+1,dfn[v]);
}
int query(int rt,int l,int r,int x){
if(l==r) return tree[rt].val;
int mid=(l+r)>>1;
pushdown(rt,l,r);
if(x<=mid) return query(rt<<1,l,mid,x);
else return query(rt<<1|1,mid+1,r,x);
}
void Solve(){
scanf("%d%d",&n,&m);
for(int i=1,x,y;i<n;++i){
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
dfs1(1,0);
dfs2(1,1);
char ccc[5];
for(int i=1,x,y;i<=m;++i){
scanf("%s%d%d",ccc,&x,&y);
if(ccc[0]=='P') Modify(x,y);
else{
int s=max(dfn[x],dfn[y]);
printf("%d\n",query(1,1,n,s));
}
}
}
int main(){
Solve();
return 0;
}
11.luogu P3398 仓鼠找sugar
前言:
感觉是个树上的结论题吧,最大的障碍不是树剖。
解析:
首先有一个性质,如果树上两条路径 \((u,v)\) 与 \((x,y)\) 有交点,那么必有\(Lca(u,v)\)在路径\((x,y)\)上,或\(Lca(x,y)\)在路径\((u,v)\)上。
反过来说,如果\(Lca(u,v)\)不在路径\((x,y)\)上,且\(Lca(x,y)\)不在路径\((u,v)\)上,那么两条路径一定没有交点。
证明:
首先,设\(Lca(u,v)=w,Lca(x,y)=z\),且\(z\)不在\((u,v)\)上;
1.\(z\)在\(w\)上方(\(z\)的深度小于\(w\))
大概就是这个样子好丑的图
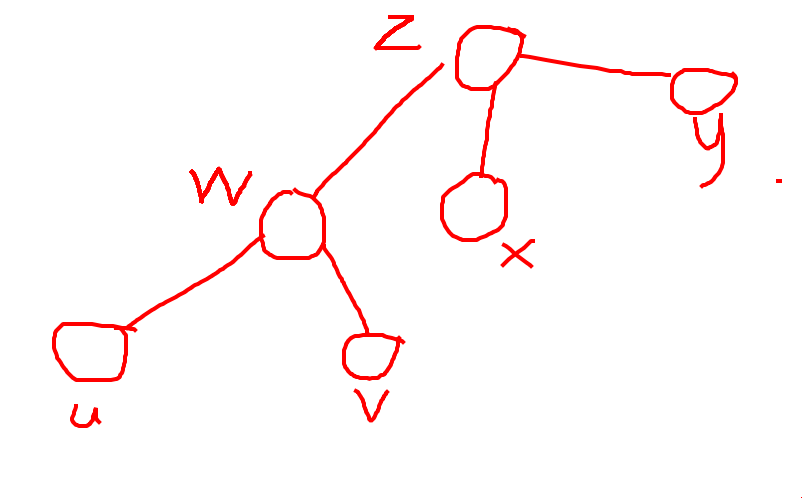
如果想让两条路径有交点,那么\(x,y\)其中一个点至少要在以\(w\)为根的子树上。
但是,如果\(x\)(或\(y\))在以\(w\)为根的子树上,必有\(w\)在\((x,z)\)或\((y,z)\)上,与我们的假设矛盾。
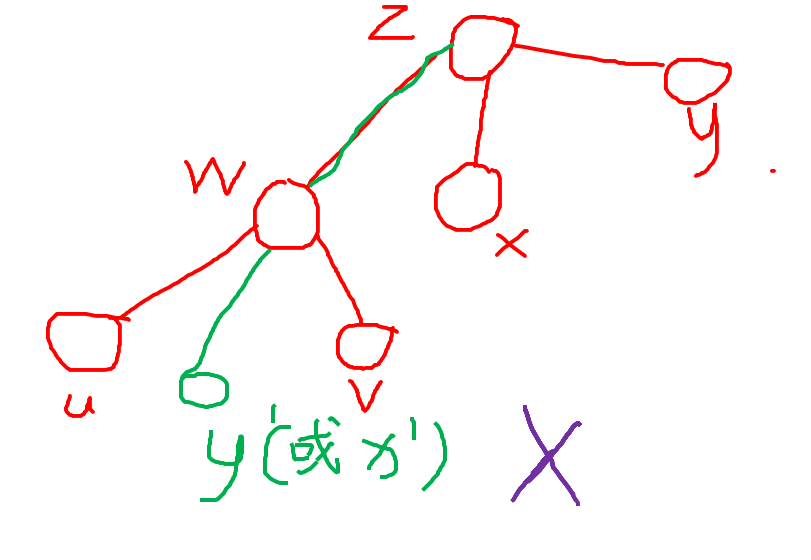
所以,如果\(z\)在\(w\)上方,两条路径一定没有交点。
2.\(z\)的深度等于\(w\)。
这个就很显然。首先为了满足前提,\(w\)一定不能等于\(z\)。
然后就会发现,\(w\)和\(z\)一定分处不同的子树中,那么显然无交点。
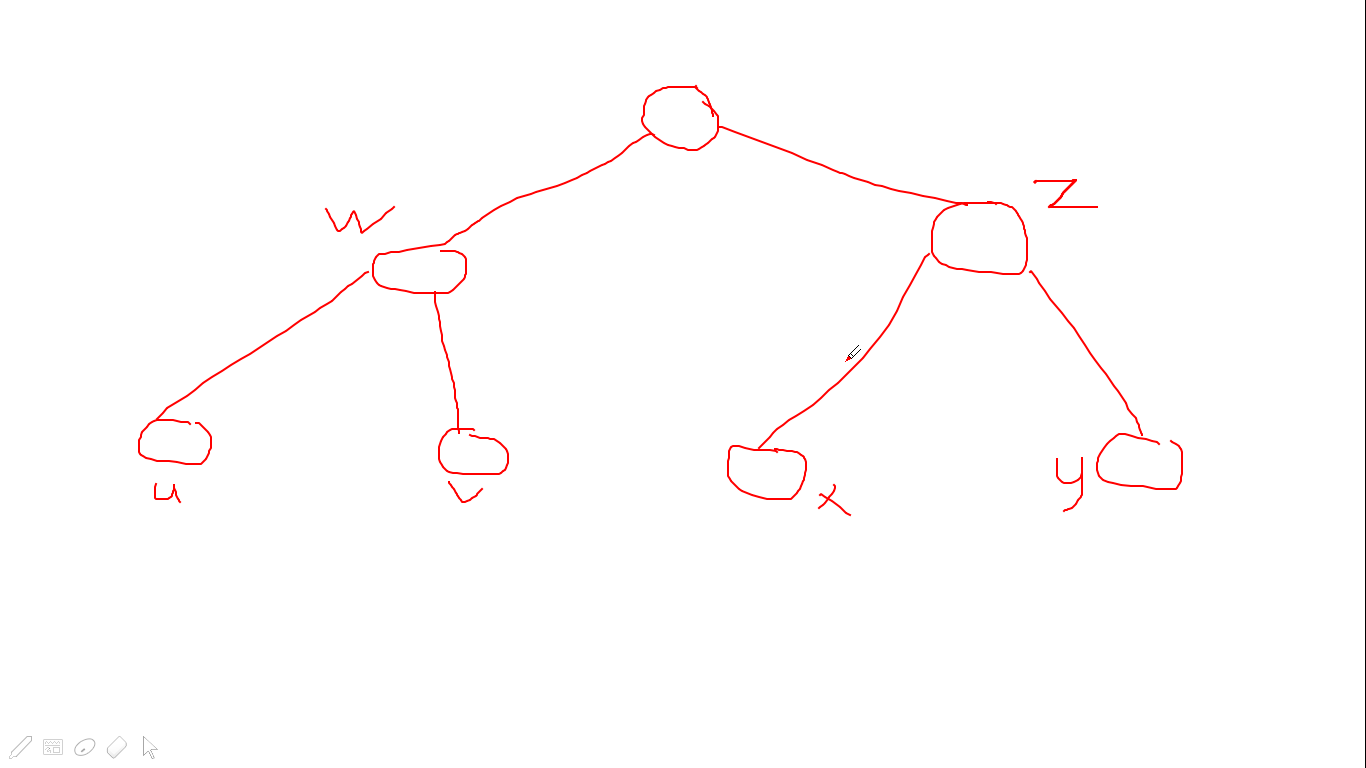
3.\(z\)的深度大于\(w\)
此时交换\((x,y)\)和\((u,v)\),变成第一种情况。
然后貌似就证完了?我们现在证明了“如果\(Lca(u,v)\)不在路径\((x,y)\)上,且\(Lca(x,y)\)不在路径\((u,v)\)上,那么两条路径一定没有交点。”
也就是说,“\(Lca(u,v)\)在路径\((x,y)\)上,或\(Lca(x,y)\)在路径\((u,v)\)上”,这是“两条路径有交点”的必要条件。
其次,只要“\(Lca(u,v)\)在路径\((x,y)\)上,或\(Lca(x,y)\)在路径\((u,v)\)上”,两条路径就一定有交点。(显然,交点至少有一个,就是LCA本身啊)
也就是说,“\(Lca(u,v)\)在路径\((x,y)\)上,或\(Lca(x,y)\)在路径\((u,v)\)上”,还是“两条路径有交点”的充分条件。
于是我们惊奇地发现,这两个条件竟然是等价的!
代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn=100000+10;
struct node{
int to,next;
}edge[maxn<<1];
int head[maxn],dfn[maxn],top[maxn],size[maxn],fa[maxn],son[maxn],depth[maxn],tree[maxn<<2];
int n,cnt,q,Time;
void add(int from,int to){
edge[++cnt].to=to;
edge[cnt].next=head[from];
head[from]=cnt;
}
void dfs1(int u,int f){
fa[u]=f;
size[u]=1;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==f) continue;
depth[v]=depth[u]+1;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
void dfs2(int u,int t){
top[u]=t;
dfn[u]=++Time;
if(son[u]) dfs2(son[u],t);
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
void build(int rt,int l,int r){
if(l==r){
tree[rt]=1;
return;
}
int mid=(l+r)>>1;
build(rt<<1,l,mid);
build(rt<<1|1,mid+1,r);
tree[rt]=tree[rt<<1|1]+tree[rt<<1];
}
int Lca(int u,int v){
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
u=fa[top[u]];
}
if(depth[u]>depth[v]) swap(u,v);
return u;
}
int query(int rt,int l,int r,int s,int t){
if(s<=l&&r<=t) return tree[rt];
int mid=(l+r)>>1;
if(t<=mid) return query(rt<<1,l,mid,s,t);
if(s>mid) return query(rt<<1|1,mid+1,r,s,t);
return query(rt<<1,l,mid,s,t)+query(rt<<1|1,mid+1,r,s,t);
}
int Query(int u,int v){
int res=0;
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
res+=query(1,1,n,dfn[top[u]],dfn[u]);
u=fa[top[u]];
}
if(u==v) return res;
if(depth[u]>depth[v]) swap(u,v);
res+=query(1,1,n,dfn[u]+1,dfn[v]);
return res;
}
bool Judge(int u,int v,int w){//w是否在u,v路径上;
return Query(u,v)==Query(u,w)+Query(v,w) ;
}
bool get_ans(int a,int b,int c,int d){
int x=Lca(a,b);
if(Judge(c,d,x)) return 1;
x=Lca(c,d);
if(Judge(a,b,x)) return 1;
return 0;
}
void Solve(){
scanf("%d%d",&n,&q);
for(int i=1,x,y;i<n;++i){
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
dfs1(1,0);
dfs2(1,1);
build(1,1,n);
int a,b,c,d;
while(q--){
scanf("%d%d%d%d",&a,&b,&c,&d);
if(get_ans(a,b,c,d)) puts("Y");
else puts("N");
}
}
int main(){
Solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号