二分图学习笔记
震惊,我发现我居然不会二分图,兼职或到薄
于是看了李煜东老师的蓝书,补了补锅。
很多时候根本看不出来某道题是二分图,因此学习一下建模的技巧。
首先是二分图最大匹配。
蓝书原话:
二分图匹配的模型有两个要素:
1.节点能分成独立的两个集合,每个集合内部有0条边。(0要素)
2.每个节点只能与1条匹配边相连。(1要素)
说的竟然折磨好,简直*****

首先是这个题。一种比较常见的模型是网格里面放东西,大概每行每列只能放一个。这时可以把每一行和每一列分别抽象成一个点集。”在当前坐标放置机器人“相当于连接该行该列的一条边。匹配的性质:任意两条边都没有公共端点,在本题即为任意两个机器人没有放在同一行或同一列上。因此找到最大匹配即为最终答案。
具体实现的话,因为有墙的存在,打破了”每行每列只能放一个“的性质。因此可以考虑把行和列重新标号,把在同一列(行)的两个墙中间的格子编为一行(列)。这样就能满足性质了。
代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn=50+10,maxm=2500+10;
char c[maxn][maxn];
int n,m,cnt,cnth,cntl,tot,ans;
struct Node{
int x,y;
}a[maxn][maxn];
int head[maxm],match[maxm],vis[maxm];
struct node{
int to,next;
}edge[maxm<<1];
void add(int from,int to){
edge[++cnt].to=to;
edge[cnt].next=head[from];
head[from]=cnt;
}
bool find(int u){
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(!vis[v]){
vis[v]=1;
if(!match[v]||find(match[v])){
match[v]=u;
return true;
}
}
}
return false;
}
void Solve(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i) scanf("%s",c[i]+1);
cnth=cntl=1;
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
if(c[i][j]=='o') a[i][j].x=cnth;
else if(c[i][j]=='#'&&j!=m) cnth++;
}
cnth++;
}
for(int j=1;j<=m;++j){
for(int i=1;i<=n;++i){
if(c[i][j]=='o') a[i][j].y=cntl;
else if(c[i][j]=='#'&&i!=n) cntl++;
}
cntl++;
}
tot=cntl+cnth;
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
if(c[i][j]=='o'){
add(a[i][j].x,a[i][j].y+cnth);
add(a[i][j].y+cnth,a[i][j].x);
}
}
}
for(int i=1;i<=tot;++i){
memset(vis,0,sizeof(vis));
if(find(i)) ans++;
}
printf("%d",ans/2);
}
int main(){
freopen("robots.in","r",stdin);
freopen("robots.out","w",stdout);
Solve();
return 0;
}
然后是这个:
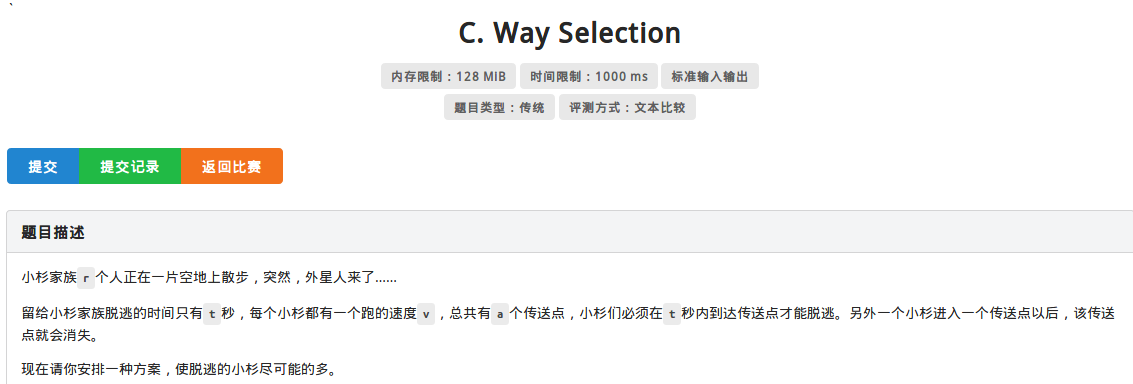
我们用蓝书的思想来套一下这道题:
分别把人和传送点抽象成一个点集,这两个集合之间显然没有连边。满足”0要素“。而每个人只会进入一个传送门,每个传送门又都只会被一个人进入。满足”1要素“。
连边跑匈牙利即可。
然后取得了71分的好成绩?

我一看



不 愧 是 我
AC代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn=20000+10;
int r,a,cnt,ans;
struct node{
double x,y;
}d[maxn],p[maxn];
int head[maxn<<1],match[maxn<<1];
bool vis[maxn<<1];
double t;
struct Node{
int to,next;
}edge[maxn<<2];
void add(int from,int to){
edge[++cnt].to=to;
edge[cnt].next=head[from];
head[from]=cnt;
}
bool find(int u){
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(!vis[v]){
vis[v]=1;
if(!match[v]||find(match[v])){
match[v]=u;
return true;
}
}
}
return false;
}
void Solve(){
scanf("%d%d%lf",&r,&a,&t);
for(int i=1;i<=a;++i) scanf("%lf%lf",&d[i].x,&d[i].y);
for(int i=1;i<=r;++i){
double A,B,v;
scanf("%lf%lf%lf",&A,&B,&v);
for(int j=1;j<=a;++j){
double dis=sqrt((A-d[j].x)*(A-d[j].x)+(B-d[j].y)*(B-d[j].y));
if(v*t>=dis){
add(i+a,j);
add(j,i+a);
}
}
}
for(int i=1;i<=a+r;++i){
memset(vis,0,sizeof(vis));
if(find(i)) ans++;
}
printf("%d",ans/2);
}
int main(){
Solve();
return 0;
}
然后是这个:刷题的事能叫水吗
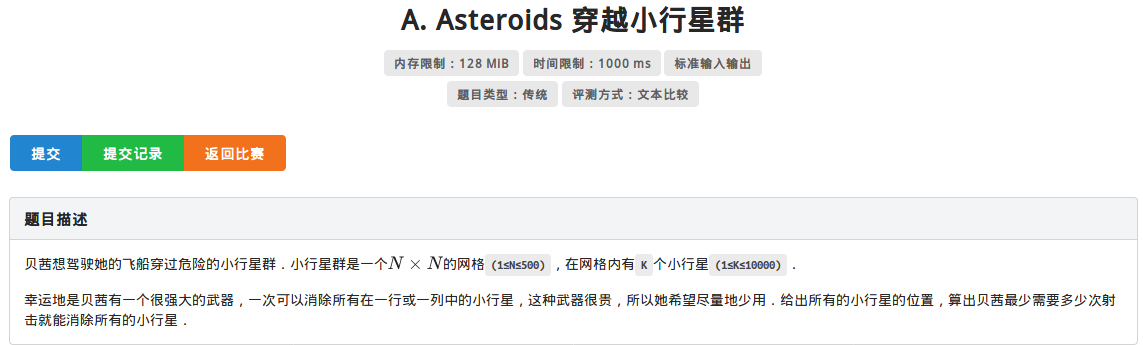
最板子的一道题,我竟然没有一眼看出来。
首先每行每列只会被”冲“一次,每个点只会被冲一次,满足”1要素“。
其次行与行之间,列与列之间没有任何关系。
因此类似robots的做法,跑一个最大匹配即可。
概念:最小点覆盖:给定一张二分图,求出一个最小的点集S,使得图中任意一条边都有至少一个端点属于S。
Konig定理:最大匹配数 = 最小点覆盖数
有了这个定理就能够解决这个题辣!
代码: 代码的事怎么能叫水篇幅呢
#include <bits/stdc++.h>
using namespace std;
const int maxm=10000+10,maxn=1000+10;
int head[maxn],vis[maxn],match[maxn];
struct node{
int to,next;
}edge[maxm<<1];
int n,m,cnt,ans;
void add(int from,int to){
edge[++cnt].to=to;
edge[cnt].next=head[from];
head[from]=cnt;
}
bool find(int u){
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(!vis[v]){
vis[v]=1;
if(!match[v]||find(match[v])){
match[v]=u;
return 1;
}
}
}
return 0;
}
void Solve(){
scanf("%d%d",&n,&m);
for(int i=1,u,v;i<=m;++i){
scanf("%d%d",&u,&v);
add(u,v+n);
add(v+n,u);
}
for(int i=1;i<=(n<<1);++i){
memset(vis,0,sizeof(vis));
if(find(i)) ans++;
}
printf("%d",ans/2);
}
int main(){
Solve();
return 0;
}
然后是这个:
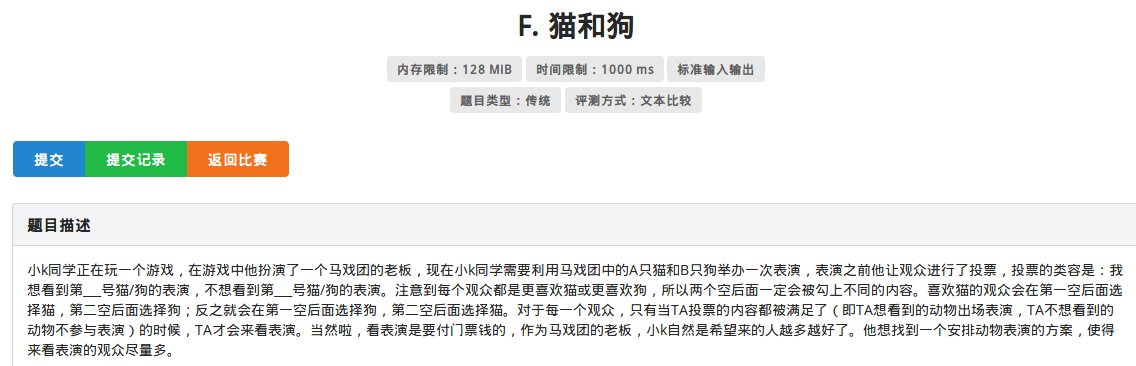
这个题稍微有点难度,第一次做的时候想把节点设置成猫和狗,然后就挂了。
事实上每只猫和狗能够满足多个人的需要,并不满足”1要素“。
而且注意到每个人都只会被一对猫和狗满足。
因此考虑把节点设置成人,把喜欢猫(狗)a的与不喜欢猫(狗)a的人进行连边。
概念:二分图的独立集:任意两点之间都没有边相连的点集。
定理:设G是有n个节点的二分图,G的最大独立集的大小等于n减去最大匹配数。
然后求最大独立集即可。
代码:
#include <bits/stdc++.h>
using namespace std;
const int maxm=10000+10;
struct node{
int next,to;
}edge[maxm<<1];
int head[maxm<<1],vis[maxm<<1],match[maxm<<1];
int cnt,n,m,k,ans;
char s1[maxm<<1][10],s2[maxm<<1][10];
void add(int from,int to){
edge[++cnt].to=to;
edge[cnt].next=head[from];
head[from]=cnt;
}
bool find(int u){
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(!vis[v]){
vis[v]=1;
if(!match[v]||find(match[v])){
match[v]=u;
return true;
}
}
}
return false;
}
void Solve(){
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=k;++i) scanf("%s%s",s1[i],s2[i]);
for(int i=1;i<=k;++i){
for(int j=1;j<=k;++j){
if(i==j) continue;
if(strcmp(s1[i],s2[j])==0){
add(i,j);
add(j,i);
}
}
}
for(int i=1;i<=k;++i){
memset(vis,0,sizeof(vis));
if(find(i)) ans++;
}
printf("%d",k-ans/2);
}
int main(){
Solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号