方阵里面的dp
打了一场luogu的信心赛,惊讶地发现我不会T2,感觉像这样在矩阵里面的dp看起来很套路的样子,但是仔细想想还是有很多需要注意的细节。
又想到之前貌似也考过一些类似的题目 然而我并没有改 ,于是打算补补锅。
目前大概想到几道题,慢慢写吧。
luogu P1006 传纸条 && 小集训模拟赛5 方格取数
很简单的两道题。注意到在“方格取数”中,因为每个方格的数字只能取一次,因此一定不会走重复路线(当然是在所有数字都大于0的情况下)。那就和“传纸条”是同一道题了。
数组可以开4维,3维,貌似还有二维?因为数据范围太小就懒得写优化了。(数据范围大的话貌似就要用网络流了,本Orzer不会)
代码:
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ll;
int a[25][25],vis[25][25],dp[25][25][25][25];
void Solve(){
int n;scanf("%d",&n);
int o,u,r;
while(1){
scanf("%d%d%d",&o,&u,&r);
if(!o&&!u&&!r) break;
a[o][u]=r;
}
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
for(int k=1;k<=n;++k){
for(int x=1;x<=n;++x){
if((i+j)!=(k+x)) continue;
dp[i][j][k][x]=max(max(dp[i-1][j][k-1][x],dp[i][j-1][k-1][x]),max(dp[i-1][j][k][x-1],dp[i][j-1][k][x-1]));
if(i==k) dp[i][j][k][x]+=a[i][j];
else dp[i][j][k][x]=dp[i][j][k][x]+a[i][j]+a[k][x];
}
}
}
}
printf("%d",dp[n][n][n][n]);
}
int main(){
Solve();
return 0;
}
小集训模拟赛12 T2 小象与老鼠
比上面的方格取数稍微难一点。因为每个点对答案造成的贡献不仅仅是这个格子的数,还有四连通的格子。dp时候要考虑去重的问题。
具体是要记录每一个dp值是从它的上面或左面转移过来。这样分类讨论就可以去重。
代码:
代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn=1000+10;
int a[maxn][maxn];
int val[maxn][maxn],dp[maxn][maxn][2];
int n,m;
void Solve(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
scanf("%d",&a[i][j]);
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
val[i][j]=a[i+1][j]+a[i][j+1];
}
}
dp[1][1][0]=dp[1][1][1]=val[1][1]+a[1][1];
for(int i=1;i<=n;++i){//0上,1左;
for(int j=1;j<=m;++j){
if(i==1&&j==1) continue;
else if(i==1) dp[i][j][1]=dp[i][j-1][1]+val[i][j];
else if(j==1) dp[i][j][0]=dp[i-1][j][0]+val[i][j];
else{
if(i-1==1) dp[i][j][0]=dp[i-1][j][1]+val[i][j];
else dp[i][j][0]=min(dp[i-1][j][0]+val[i][j]+a[i][j-1],dp[i-1][j][1]+val[i][j]);
if(j-1==1) dp[i][j][1]=dp[i][j-1][0]+val[i][j];
else dp[i][j][1]=min(dp[i][j-1][1]+val[i][j]+a[i-1][j],dp[i][j-1][0]+val[i][j]);
}
}
}
printf("%d",min(dp[n][m][1],dp[n][m][0]));
}
int main(){
Solve();
return 0;
}
luogu P6855 「EZEC-4.5」走方格(2020.10.4 君のNOIP のCSP信心赛 T2)
刚刚做的新题。刚开始的时候觉得很套路,几分钟就把代码写出来了。调了十分钟后过不了样例之后才发现自己错了。
出题人的题解
看了题解才明白。。。我太菜了
首先显然有\(O(n^4)\) 做法。枚举所有点,尝试将其变成0即可。
然后显然可以优化到O(n^3)因为发现如果变成0的点不再原来的最长路上,那么对最终答案是没有贡献的。因此只需要枚举最长路上的点即可。
然后考虑优化。
对于最长路上的某个点,如果把它变成0。
第一种情况,如果把它变成0,它依然在最长路上。
第二种情况,其他的格子会变成最长路上的点。
那应该怎么计算呢?
可以发现,如果把一个点变成0,不影响(1,1)到这个点之前的所有点的最长路。
同时还可以发现,如果反过来想,如果把一个点变成0,也不影响这个点之后的所有点到(n,m)的最长路。
于是我们可以预处理出两个数组:
dp[i][j]表示(1,1)到(i,j)的最长路,f[i][j]表示(i,j)到(n,m)的最长路。
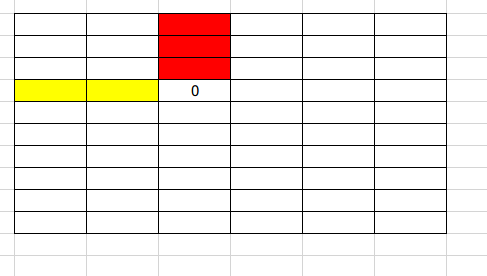
那么把f[i][j]变成0的答案就是图中黄色格子向下走,红色格子向右走的答案取max。
最后把所有f[i][j]的答案取min即可。
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=2000+10;
#define gc() (p1 == p2 ? (p2 = buf + fread(p1 = buf, 1, 1 << 20, stdin), p1 == p2 ? EOF : *p1++) : *p1++)
#define read() ({ register int x = 0, f = 1; register char c = gc(); while(c < '0' || c > '9') { if (c == '-') f = -1; c = gc();} while(c >= '0' && c <= '9') x = x * 10 + (c & 15), c = gc(); f * x; })
char buf[1 << 20], *p1, *p2;
int a[maxn][maxn];
ll f[maxn][maxn],dp[maxn][maxn];
bool vis[maxn][maxn];
int n,m;
ll ans=0x3f3f3f3f3f3f3f3f;
struct node{
int x,y;
node(){}
node(int aa,int bb){
x=aa;
y=bb;
}
};
queue <node> q;
void Solve(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
scanf("%d",&a[i][j]);
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
dp[i][j]=max(dp[i-1][j],dp[i][j-1])+a[i][j];
}
}
for(int i=n;i;--i){
for(int j=m;j;--j){
f[i][j]=max(f[i+1][j],f[i][j+1])+a[i][j];
}
}
q.push(node(n,m));
while(!q.empty()){
node t=q.front();
if(vis[t.x][t.y]) continue;
vis[t.x][t.y]=1;
q.pop();
ll x=max(dp[t.x-1][t.y],dp[t.x][t.y-1]);
if(dp[t.x-1][t.y]>dp[t.x][t.y-1] && t.x>1 ) q.push(node(t.x-1,t.y));
else if(t.y>1) q.push(node(t.x,t.y-1));
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
if(vis[i][j]){
ll res=dp[n][m]-a[i][j];
for(int k=1;k<j;++k) res=max(res,dp[i][k]+f[i+1][k]);
for(int k=1;k<i;++k) res=max(res,dp[k][j]+f[k][j+1]);
ans=min(res,ans);
}
}
}
printf("%lld\n",ans);
}
int main(){
Solve();
return 0;
}
小集训模拟赛9 T4 步步为零
土题大战Vol.0 T2 小奇的矩阵 (火星补锅系列)
这题算是比较难的。首先需要推一下柿子(推柿子的时间和你上高考数学课划水的时间成正比)
当然,但凡你没有和我一样,高二快过一半,数学只有高一上的水平,就能一眼看出来,题目里面的柿子是个方差公式的变形。
然后,根据 \(D(x)=E(x^2)-(E(x))^2\) 这个学过高考都知道的柿子,就可以推出:
\(ans=(n+m-1)\sum_{i=1}^{n+m-1}A_i^2-(\sum_{i=1}^{n+m-1}A_i^2)^2\)
然后会发现,这个柿子的值只和每一项的值和每一项的平方有关。
于是可以定义转移方程:
dp[i][j][k]表示当前走到(i,j),\(\sum_{s=1}^{i+j-1}A_s\) 的值为k,的最小的\(\sum_{s=1}^{i+j-1}A_s^2\)
然后转移就很简单啦!
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=100000+10;
#define gc() (p1 == p2 ? (p2 = buf + fread(p1 = buf, 1, 1 << 20, stdin), p1 == p2 ? EOF : *p1++) : *p1++)
#define read() ({ register int x = 0, f = 1; register char c = gc(); while(c < '0' || c > '9') { if (c == '-') f = -1; c = gc();} while(c >= '0' && c <= '9') x = x * 10 + (c & 15), c = gc(); f * x; })
char buf[1 << 20], *p1, *p2;
ll dp[40][40][2000];
int a[40][40];
int n,m;
ll ans;
void Solve(){
int T;scanf("%d",&T);
while(T--){
ans=0x3f3f3f3f3f3f3f3f;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
scanf("%d",&a[i][j]);
}
}
memset(dp,0x3f,sizeof(dp));
dp[1][1][a[1][1]]=a[1][1]*a[1][1];
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
for(int k=a[i][j];k<=1800;++k){
if(i==1&&j==1) continue;
if(i>1&&j>1) dp[i][j][k]=min(dp[i][j-1][k-a[i][j]],dp[i-1][j][k-a[i][j]])+a[i][j]*a[i][j];
else if(j==1) dp[i][j][k]=dp[i-1][j][k-a[i][j]]+a[i][j]*a[i][j];
else dp[i][j][k]=dp[i][j-1][k-a[i][j]]+a[i][j]*a[i][j];
}
}
}
for(int i=0;i<=1800;++i) if(dp[n][m][i]<=1e9) ans=min(ans,1ll*(n+m-1)*dp[n][m][i]-1ll*i*i);
printf("%lld\n",ans);
}
}
int main(){
Solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号