[HNOI2009]双递增序列(洛谷P4728)+小烈送菜(内部训练题)——奇妙的dp
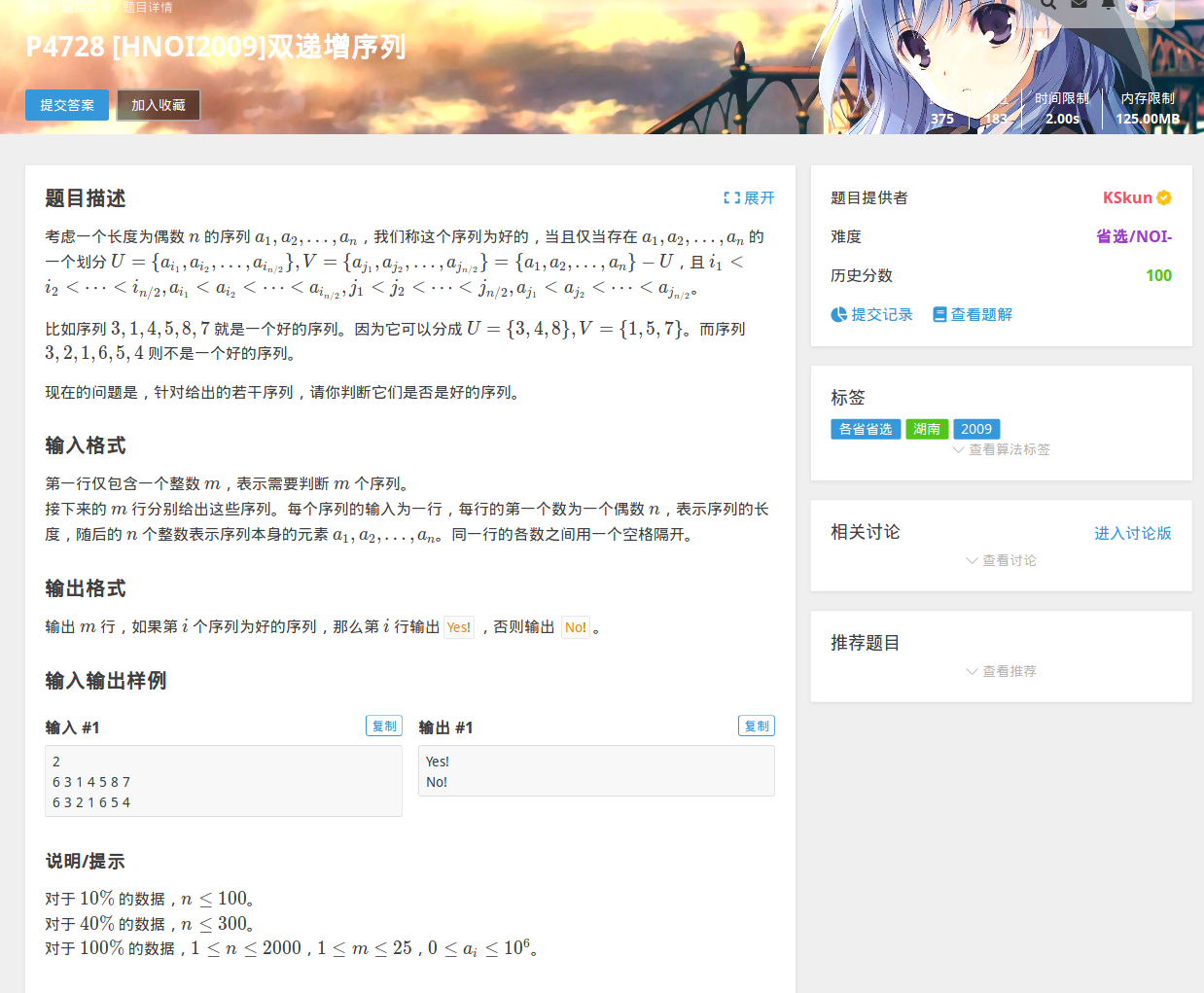
博主学习本题的经过嘤嘤嘤:
7.22 : 听学长讲(一知半解)——自己推(推不出来)——网上看题解——以为自己会了(网上题解是错的)——发现错误以后又自己推(没推出来)——给学长发邮件——得到正确解法——按着学长思路又推一遍——最后理解
(前后的“学长”不是同一个人)
7.23 : 写出代码,完善细节。
(建议改成:西 天 取 经)
首先,网上对于这道题的题解绝大部分是错误的!(比如洛谷上的部分题解)
用LIS做是不行的
玄学贪心是不行的
dp转移方程不能自圆其说是不行的
即使是AC代码也不一定是正确的(2009年的省选,数据太太太太太太太太太太太太太太水了嘤嘤嘤)
废话说完了
~~~~~~~~~~~~~~~嘤嘤嘤来自蒟蒻OIerOrzer的分割线啦嘤嘤嘤~~~~~~~~~~~~~~~~
以下为正文部分嘤嘤嘤:
考虑把一个数列分成两个集合,有a[i]的为一个集合,没有a[i]的为一个集合~
我们定义状态转移方程dp[i][j]表示对于前i个数,有a[i]的集合的长度为j,没有a[i]的集合的最后一个数的最小值为dp[i][j](神仙定义)
也就是说,现在有两个集合,其中一个有a[i],另一个没有a[i]。尝试把a[i+1]放到其中一个集合中。
1.尝试把a[i+1]放到有a[i]的集合当中。那么需要满足的先决条件就是:a[i+1]>a[i].
此时更新dp[i+1][j+1](因为把a[i]放到长度为j的集合中,于是长度++)此时没有a[i+1]的集合同时也是没有a[i]的集合,换句话来说,这个转移对没有a[i]的集合是没有改变的,所以,dp[i+1][j+1]可以直接由dp[i][j]继承过来。
2.尝试把a[i+1]放到没有a[i]的集合当中。那么需要满足的先决条件就是:a[i+1]>dp[i][j].
此时更新dp[i+1][i-j+1](原来没有a[i]的集合的长度为(i-j),把a[i+1]放进去,长度++)既然把a[i+1]放到了没有a[i]的集合中,那么,没有a[i+1]的集合的最后一个数就是a[i],于是,用a[i]去更新dp[i+1][i-j+1];
(真绕啊嘤嘤嘤)
上代码嘤嘤嘤:
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int maxn=2000+10; 4 int dp[maxn][maxn],a[maxn]; 5 int n,m; 6 void Solve(){ 7 scanf("%d",&m); 8 while(m--){ 9 scanf("%d",&n); 10 memset(dp,0x3f,sizeof(dp)); 11 memset(a,0x3f,sizeof(a)); 12 for(int i=1;i<=n;++i) scanf("%d",&a[i]); 13 dp[1][1]=-1;//因为数据中可能有0,因此不能初始化为0; 14 for(int i=1;i<=n;++i){ 15 for(int j=1;j<=i;++j){ 16 if(a[i+1]>a[i]) dp[i+1][j+1]=min(dp[i+1][j+1],dp[i][j]); 17 if(a[i+1]>dp[i][j]) dp[i+1][i-j+1]=min(dp[i+1][i-j+1],a[i]); 18 } 19 } 20 if(dp[n][n/2]>1e8) printf("No!\n"); 21 //没有更新,说明不能将原序列合法地平分成两部分,就输出No; 22 else printf("Yes!\n"); 23 } 24 } 25 int main(){ 26 Solve(); 27 return 0; 28 }
完结撒花嘤嘤嘤~(然而并没有)
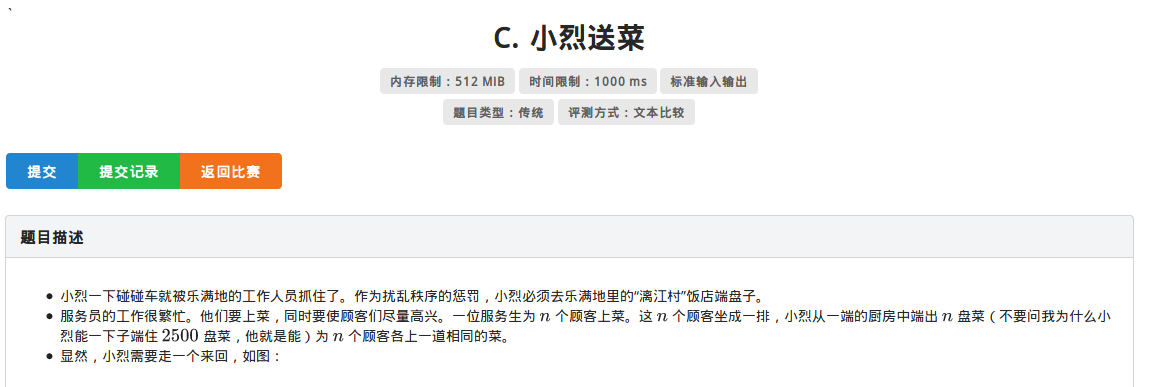
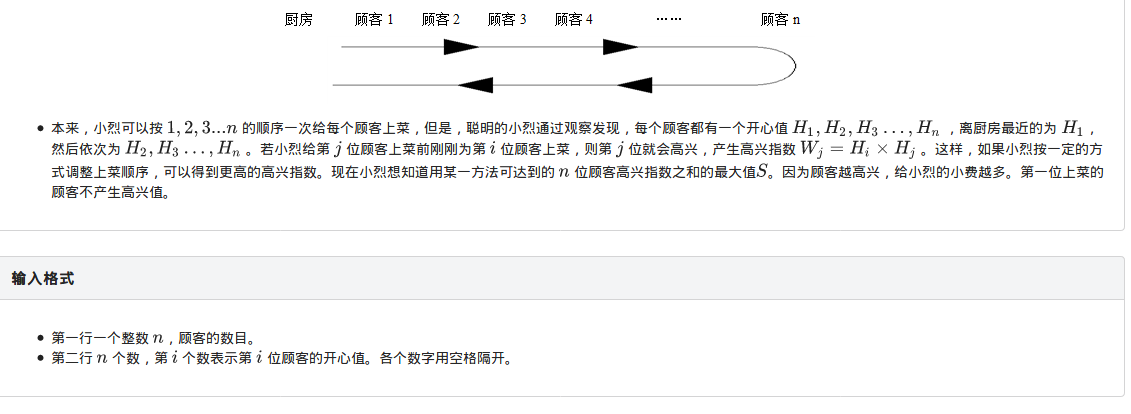
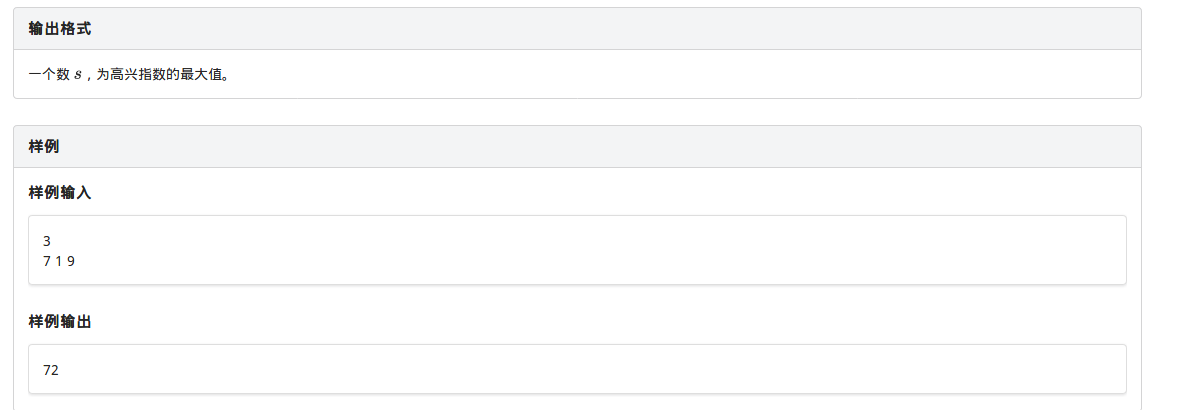

上辈子的题了(大雾)(所以这就是火星水吗)
但是在解决上一道题后会发现对于这道题会有不一样的理解~~~
我们先定义dp[i][j]表示小烈1走到i,小烈2走到j时的最大收益。且默认小烈1始终在小烈2前面,且前j个已经被送完。
换句话来说,其实根本没有小烈1和小烈2(只是我们yy出来的)或者说,并不是划分了“小烈1”和“小烈2”这两个抽象的概念,划分的应该是“送了a[i]的小烈”和“没有送a[i]的小烈”!
(woc这不就是上一道题吗,太像了好叭)
现在我们换一种表达方式来定义dp[i][j]:
dp[i][j]表示前i个客人,没有送过a[i]的小烈最后一个送的是a[j]时的最大收益。
默认j小于i,且前j个一定已经送过了(如果前j个有没有送过的,那就不合法了,因为两个小烈不能回头)
现在考虑a[i+1]由谁送。
1.由送了a[i]的小烈送。所以,没有送a[i]的小烈同样没有送a[i+1]。也就是说,这个转移完成后,没有送a[i]的小烈原来在j,现在还是在j,没有变化。
所以用(dp[i][j]+a[i]*a[i+1])更新(dp[i+1][j])。
2.由没有送a[i]的小烈送。所以,送了a[i]的小烈没有送a[i+1]。也就是说,没有送a[i+1]的小烈最后一个送的是a[i]!
所以用(dp[i][j]+a[j]*a[i+1])更新(dp[i+1][i]).
(和刚才那个一样绕嘤嘤嘤)
上代码:

1 #include <bits/stdc++.h> 2 using namespace std; 3 const int maxn=2500+10; 4 int dp[maxn][maxn],a[maxn],ans; 5 void Solve(){ 6 int n;scanf("%d",&n); 7 for(int i=1;i<=n;++i) scanf("%d",&a[i]); 8 for(int i=1;i<=n;++i){ 9 for(int j=0;j<i;++j){//j的范围要搞清楚哦; 10 dp[i+1][j]=max(dp[i+1][j],dp[i][j]+a[i]*a[i+1]); 11 dp[i+1][i]=max(dp[i+1][i],dp[i][j]+a[j]*a[i+1]); 12 } 13 } 14 for(int i=0;i<n;++i) ans=max(ans,dp[n][i]+a[i]*a[n]); 15 /*现实中的小烈是从1走到n,又从n回去,在dp方程里面我们把一个小烈拆成了两个, 16 其中一个表示现实中正向走的部分,另一个表示现实中反向走的部分(但是令这一个 17 反向走的小烈反过来走,就是正着走)也就是说,当现实中小烈走到n,开始返回的 18 时候,a[n]与dp方程中定义的小烈2经过的最后一个a[i](也就是反着走的第一个 19 a[i])是要产生一个值的,而这个值要加到答案里面才能得到最终结果*/ 20 printf("%d",ans); 21 } 22 int main(){ 23 Solve(); 24 return 0; 25 }
完结撒花花!!!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号