[51nod1482]部落信号 单调栈
题解:
可以发现这是一道单调栈的题目,首先来考虑数字没有重复时如何统计贡献。
因为这是一个环,而如果我们从最高的点把环断开,并把最高点放在链的最后面(顺时针移动),那么因为在最高点两侧的点无法互相看见,相当于就把环转化为链的问题了。
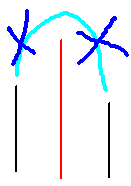
因此维护递减的单调栈,如果进来的点比栈顶高就弹出并统计1的贡献。
但是这样会有遗漏,我们观察什么情况下会遗漏。
因为是从1开始遍历,因此在前面的节点在遍历到n时完全有可能已经被弹走了,然而因为这是一个环,断开点(最高点)说不定还可以回头看见它。因此这种情况会被遗漏。
但如果又反着统计又会统计重复,因此考虑不统计最高点的贡献,然后最后再暴力跑2遍统计断开点的贡献。
但是数字可能有重复,怎么办?
重复数字会带来很多细节上的问题,比如8333中有5的贡献,而直接弹走显然统计不到5.又比如最大值可能有很多个,因此会将整个数列分为很多小段,,,等等诸如此类。
因此对于第一种情况,我们记录一下当前栈中每个数字有多少个,因为数字可能很大,但个数不多,因此一开始要离散化一下。
对于第二种情况,可以在最后暴力统计一下最高点两两搭配的方案数。
细节很多,注意调试&对拍

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define R register int 4 #define AC 1001000 5 #define LL long long 6 7 int n, id, k, maxn, num, last, cnt; 8 LL ans; 9 int ss[AC], t[AC], tot[AC]; 10 int s[AC], top; 11 bool vis[AC]; 12 13 inline int read() 14 { 15 int x = 0;char c = getchar(); 16 while(c > '9' || c < '0') c = getchar(); 17 while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); 18 return x; 19 } 20 21 inline void upmax(int &a, int b) 22 { 23 if(b > a) a = b; 24 } 25 26 inline int get(int x) 27 { 28 if(x < 1) x += n; 29 return x > n ? x - n : x; 30 } 31 32 int half(int x) 33 { 34 int l = 1, r = cnt; 35 while(l < r) 36 { 37 int mid = (l + r) >> 1; 38 if(ss[mid] == x) return mid; 39 else if(ss[mid] < x) l = mid + 1; 40 else r = mid - 1; 41 } 42 return l; 43 } 44 45 void pre() 46 { 47 n = read(); 48 for(R i = 1; i <= n; i ++) 49 { 50 ss[i] = read(); 51 if(ss[i] > k) id = i, k = ss[i], num = 1; 52 else if(ss[i] == k) ++ num; 53 } 54 id = get(id + 1); 55 for(R i = 1; i <= n; i ++) t[i] = ss[get(id + i - 1)]; 56 sort(ss + 1, ss + n + 1); 57 for(R i = 1; i <= n; i ++) 58 if(ss[i] != ss[i + 1]) ss[++cnt] = ss[i]; 59 for(R i = 1; i <= n; i ++) t[i] = half(t[i]); 60 k = cnt; 61 } 62 63 /*8 64 3 1 5 7 1 1 7 8 */ 65 void work() 66 { 67 for(R i = 1; i < n; i ++)//不统计中断处的 68 { 69 int tmp = (top && s[1] != t[i]); 70 // printf("%d\n", top); 71 while(top && s[top] < t[i]) -- tot[s[top]], -- top, ++ ans; 72 if(top && s[top] != t[i]) ++ ans; 73 ++ tot[t[i]], s[++top] = t[i]; 74 if(tot[t[i]] - 1) ans += tot[t[i]] - 1 + tmp; 75 // printf("%d\n", top); 76 } 77 for(R i = 1; i <= n; i ++) 78 { 79 if(t[i] == k) break; 80 if(vis[i]) continue; 81 if(t[i] >= maxn && !vis[i]) ++ ans, vis[i] = true; 82 upmax(maxn, t[i]); 83 } 84 maxn = 0; 85 for(R i = n - 1; i; i --) 86 { 87 if(t[i] == k) break; 88 if(t[i] >= maxn && !vis[i]) ++ ans, vis[i] = true; 89 upmax(maxn, t[i]); 90 } 91 if(num > 1) ans += num * (num - 1) / 2 - (num - 1) * (num - 2) / 2; 92 printf("%lld\n", ans); 93 } 94 95 int main() 96 { 97 // freopen("in.in", "r", stdin); 98 pre(); 99 work(); 100 // fclose(stdin); 101 return 0; 102 }




