[国家集训队]最长双回文串 manacher

～～～题面～～～

题解：

首先有一个直观的想法，如果我们可以求出对于位置i的最长后缀回文串和最长前缀回文串，那么我们枚举分界点然后合并前缀和后缀不就可以得到答案了么？

所以我们的目标就是求出这两个数列，

我们令f[i] 表示以i为结尾的最长回文后缀的长度，g[i]表示以i为开头的最长回文后缀的长度。

由于要找回文串，因此我们先想到manacher。

然后我们可以发现对于这样一个串：

原串：xxxxxxxxxx

新串：#x#x#x#x#x#x#x#x#x#x#

我们可以观察到，假设这时我们已经求出了f和g，那么对于任意位置而言，合并出的最长双回文串中，都是“偶串”，且有一半是'#',一半是原串。

因此我们可以直接合并f[i-1] 和 g[i],并用ans记录最大值，那么这时真正的答案就是ans / 2.

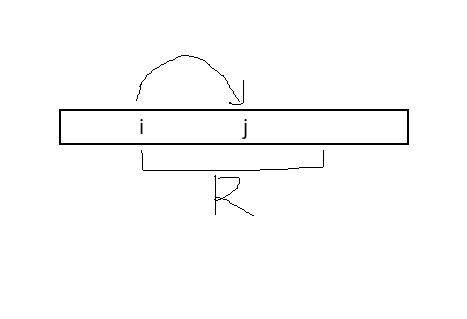
假设我们manacher已经求到了第i位，此时i的最长回文半径是R，且j已经被包括在R里面了，那么显然i对j的贡献是(j - i) * 2 + 1。

而因为贡献只和i与j的位置有关，并且我们的i是从1开始，逐渐递增的，因此对于任意一个j，第一次将它更新的i必然可以产生最优解，因此每个j会且仅会被更新一次。

而被更新的j显然也是递增的，因为如果j后面的k已经被更新的话，说明之前已经有一个i可以使得k被覆盖在内了。那么j既然在k前面，肯定也被覆盖过了，

因此求出f[j]时，j肯定是递增的（也就是说肯定是先求出前面的在求出后面的），因此我们可以直接维护一个指针t（这个指针只是字面上的指针），表示当前已经更新到了t，

一旦被覆盖的MaxRight > t,我们就直接用当前的i来更新t。

对于前缀回文串，我们直接把字符串翻转过来，然后再做一遍相同的操作，再把得到的数组反转回来就可以了

#include<bits/stdc++.h>
using namespace std;
#define R register int 
#define AC 202000
/*处理出前缀半径和后缀半径，然后合并。可以发现，在扩充了数列之后（#），
获取的最长双回文串一定是偶串，且# 和 真实字符数量相同。
因此ans就是合并后的最长长度/2*/
int n, pos, maxn, ans;
int f[AC], g[AC], tmp[AC], r[AC];
char s[AC], p[AC];

void pre()//读入
{
    scanf("%s", s + 1);
    n = strlen(s + 1);
    for(R i = n; i; --i) s[i * 2] = s[i];
    n = 2 * n + 1;
    for(R i = 1; i <= n; i += 2) s[i] = '#';
    for(R i = 1; i <= n; i++) p[i] = s[n - i + 1];//把原串倒过来做一遍就是后缀了
    s[0] = p[0] = '$', s[n + 1] = p[n + 1] = '$';
}

void build()//处理出前缀半径和后缀半径
{
    int t = 0;
    pos = maxn = 0;
    for(R i = 1; i <= n; i++)
    {
        r[i] = maxn > i ? min(r[2 * pos - i], maxn - i + 1) : 1;
        while(s[i - r[i]] == s[i + r[i]]) ++r[i];
        if(i + r[i] - 1 > maxn)
        {
            maxn = i + r[i] - 1, pos = i;
            if(maxn > t)//更新后缀
            {
                for(R j = t + 1; j <= maxn; j++) f[j] = (j - i) * 2 + 1;    
                t = maxn;
            }
        }
    }
    pos = maxn = t = 0;
    for(R i = 1; i <= n; i++)
    {
        r[i] = maxn > i ? min(r[2 * pos - i], maxn - i + 1) : 1;
        while(p[i - r[i]] == p[i + r[i]]) ++r[i];
        if(i + r[i] - 1 > maxn)
        {
            maxn = i + r[i] - 1, pos = i;
            if(maxn > t)//更新后缀
            {
                for(R j = t + 1; j <= maxn; j++) tmp[j] = (j - i) * 2 + 1;    
                t = maxn;
            }
        }
    }
    for(R i = 1; i <= n; i++) g[i] = tmp[n - i + 1];
//    for(R i = 1; i <= n; i++) printf("%d ", f[i]);
//    printf("\n");
}

inline void upmax(int &a, int b)
{
    if(b > a) a = b;
}

void work()//合并
{
    for(R i = 1; i <= n; i++)
        upmax(ans, f[i - 1] + g[i]);
    printf("%d\n", ans/2);
}

int main()
{
    freopen("in.in", "r", stdin);
    pre();
    build();
    work();
    fclose(stdin);
    return 0;
}