[CQOI2017]老C的方块 网络流

～～～题面～～～

题解：

做这题做了好久，，，换了4种建图QAQ

首先我们观察弃疗的形状，可以发现有一个特点，那就是都以一个固定不变的特殊边为中心的，如果我们将特殊边两边的方块分别称为s块和t块，

那么我们可以观察到，s块和t块永远是在中心位置，而其他两块则是紧邻s块和t块，一边一个。

所以我们要考虑将这个图像用一根线串起来，这样跑最小割才能割最小的边，

那么如何做到一条边割几个图形呢？

首先我们观察到一个非st方块本来就可以属于多个图形，因此也会有多条连边，因此我们只需要对每个方块拆点，限制其只能割一次就可以了。

一开始我选择的连图方式是：

以特殊边左边为s块，右边为t块，s连向s块，t块连向t（s块和t块名字来源），s块连向四周的非t块，t块四周的非s块连向它，s块四周的非t块连向t块四周的非s块。

但这样为什么这样不行呢？

我们可以观察到这样一种情况，

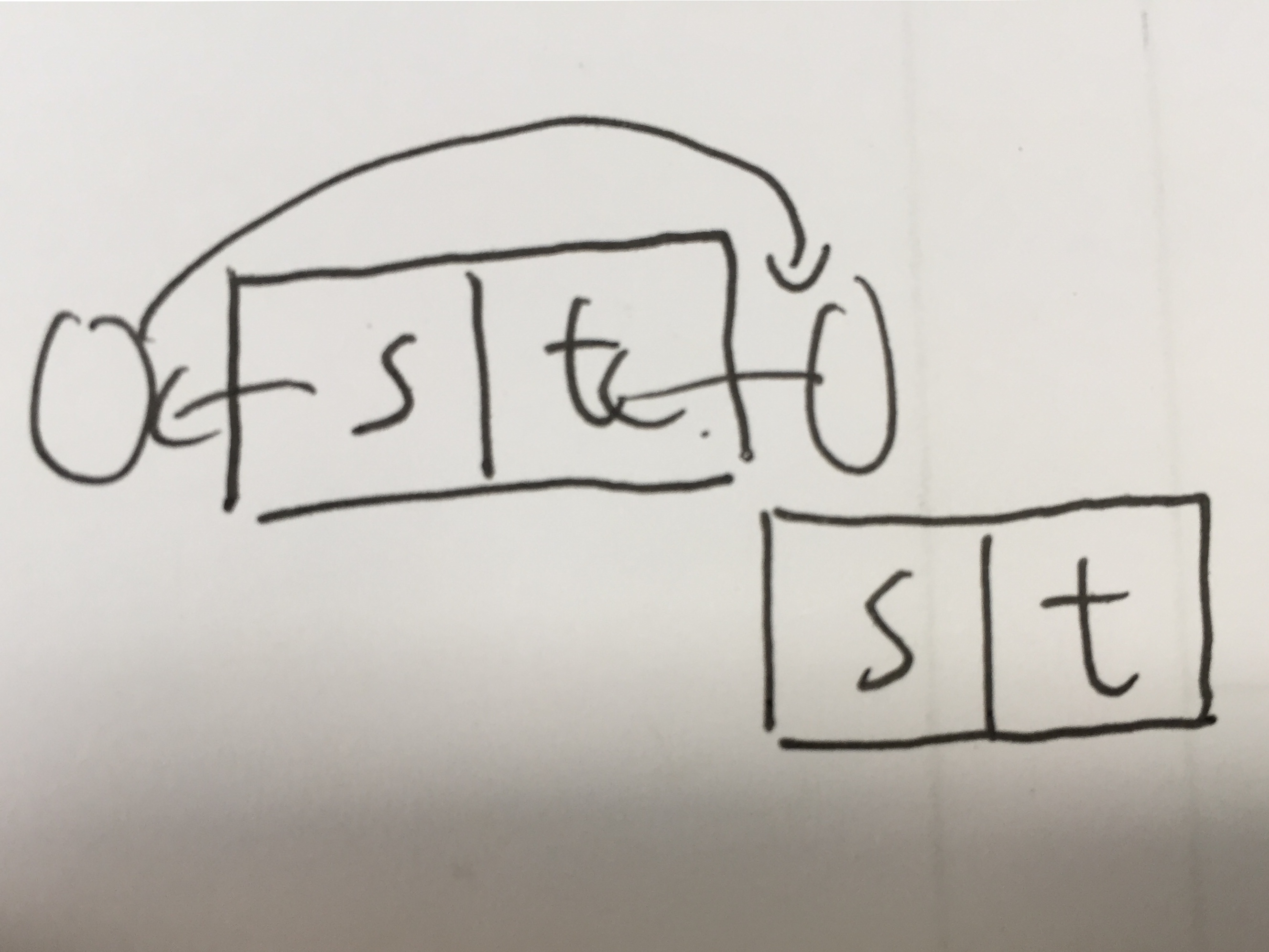
可以发现，右边的小圆圈同时处在s块和t块周围，那么由于扮演了两个角色，这就有可能导致右边的s块的流量流到左边的t块里，于是就出现了不合法情况。

…………

遂交换偶行的s块和t块。

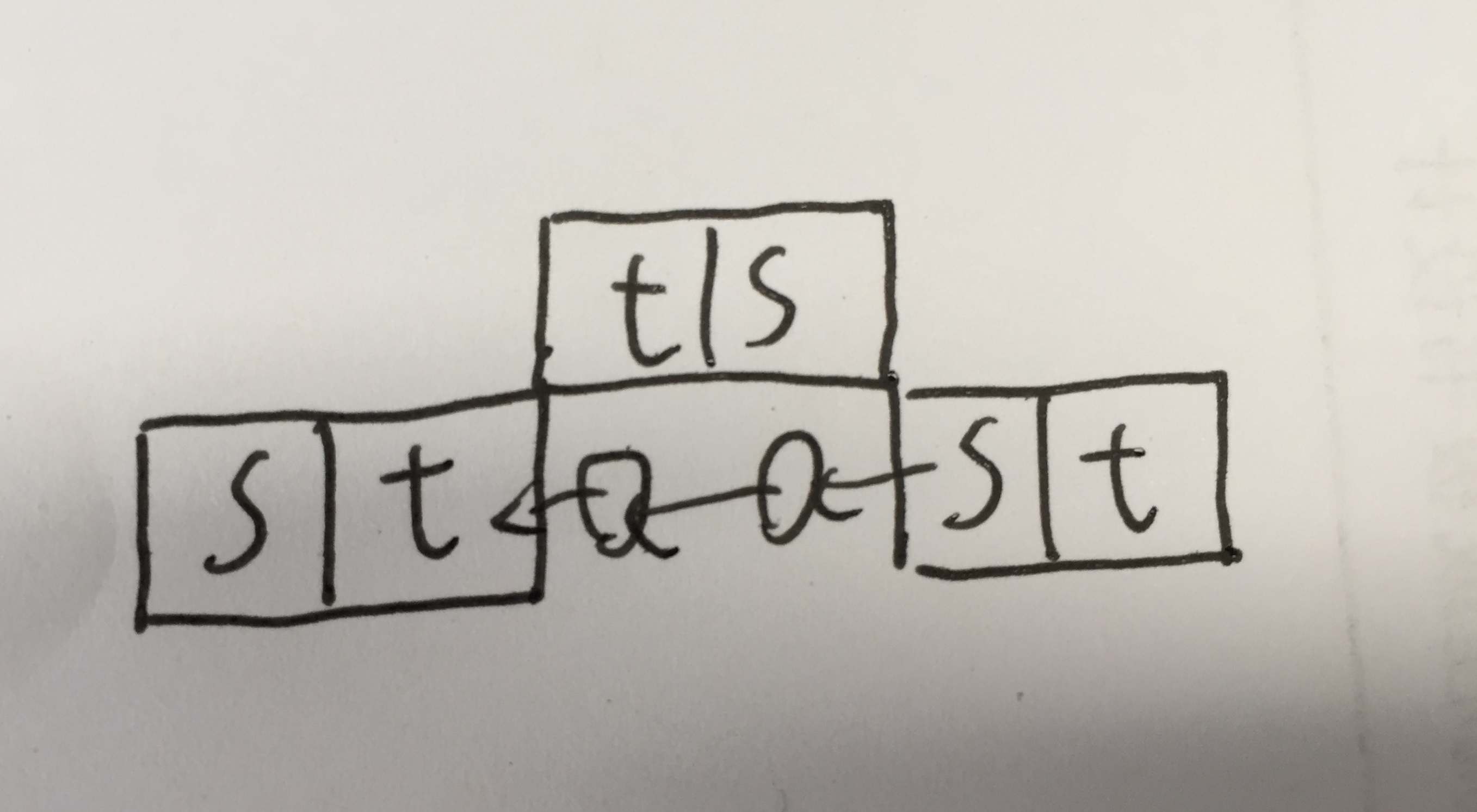
可以发现，右边的s块和左边的t块构成了一个不合法图形，那么这是为什么？

显然是上面反过来的t块和s块在勾桥搭线。。。。

那怎么办？

我们再观察一下图形。既然所有图形都是以s块和t块为中心，那么这两块显然是更加稳定的，因此我们不再用其他块作为中转块，而是采用以s块和t块为中转。

即：

s ---> s块周围的块 ----> s块 ---> t块 ---> t块周围的块

经验证，可以满足要求。

我是强行暴力人工分类讨论建图的。。。因此代码很长，建图就有60行。。。。

#include<bits/stdc++.h>
using namespace std;
#define R register int
#define inf 2139062143
#define getchar() *o++
#define AC 200100
#define ac 1700000

char READ[7001000], *o = READ;
int n, x, ans, s, t, addflow, X, Y;
int last[AC], good[AC], have[AC], c[AC], power[AC];
int q[AC], head, tail;
int date[ac], Next[ac], haveflow[ac], Head[AC], tot = 1;

struct point{
    int x, y;
}p[AC];

bool operator < (point a, point b)
{
    if(a.x != b.x) return a.x < b.x;
    else return a.y < b.y;
}

map<point, int> m;
 
inline int read()
{
    int x=0;char c=getchar();
    while(c > '9' || c < '0') c = getchar();
    while(c >= '0' && c <= '9') x=x*10+c-'0',c=getchar();
    return x;
}

inline void add(int f, int w, int S)
{
    date[++tot] = w, Next[tot] = Head[f], haveflow[tot] = S, Head[f] = tot;
    date[++tot] = f, Next[tot] = Head[w],/* haveflow[tot] = 0,*/ Head[w] = tot;
//    printf("%d ---> %d %d\n", f, w, S);
}

void pre()
{
    X = read(), Y = read(), n = read();
    s = n * 2 + 1, t = s + 1;
    for(R i=1;i<=n;i++)
    {
        p[i].y = read(), p[i].x = read(), power[i] = read();//注意行列是反的！
        m[p[i]] = i;//编号
    }
}

void build()//暴力枚举加边
{
    int x, y;
    for(R i=1;i<=n;i++)//枚举方块，只连出边
    {
        add(i, n + i, power[i]);//拆点连边
        x = p[i].x, y = p[i].y;
        if(x % 2)//按奇偶行分类 
        {
            if(y % 2)//按奇偶列分类（可能为s or t右）
            {//因为2 = 2 * 1, 6 = 2 * 3 .... 所以有余数就说明是s
                if(((y + 1) / 2) % 2)//有余数所以是s    
                {//跟旁边的t连上
                    if(m[(point){x, y + 1}]) add(i + n, m[(point){x, y + 1}], inf);
                }
                else add(i + n, t, inf);//不然就要连向t了    
            }
            else//不然就是s左的 or t
            {
                if((y / 2) % 2) 
                {
                    if(m[(point){x, y + 1}]) add(i + n, m[(point){x, y + 1}], inf);//如果有余数说明是t
                    if(m[(point){x + 1, y}]) add(i + n, m[(point){x + 1, y}], inf);
                    if(m[(point){x - 1, y}]) add(i + n, m[(point){x - 1, y}], inf);
                }
                else//不然属于s周围的
                {
                    if(m[(point){x, y + 1}]) add(i + n, m[(point){x, y + 1}], inf);
                    if(m[(point){x + 1, y}]) add(i + n, m[(point){x + 1, y}], inf);
                    if(m[(point){x - 1, y}]) add(i + n, m[(point){x - 1, y}], inf);
                    add(s, i, inf);//注意s周围的要连s
                }
            }
        }
        else //偶行
        {
            if(y % 2)//奇列，t or s右
            {
                if(((y + 1) / 2) % 2)//如果有余数说明是s右
                {
                    if(m[(point){x, y - 1}]) add(i + n, m[(point){x, y - 1}], inf);
                    if(m[(point){x + 1, y}]) add(i + n, m[(point){x + 1, y}], inf);
                    if(m[(point){x - 1, y}]) add(i + n, m[(point){x - 1, y}], inf);        
                    add(s, i, inf);        
                }
                else
                {
                    if(m[(point){x, y - 1}]) add(i + n, m[(point){x, y - 1}], inf);//如果有余数说明是t
                    if(m[(point){x + 1, y}]) add(i + n, m[(point){x + 1, y}], inf);
                    if(m[(point){x - 1, y}]) add(i + n, m[(point){x - 1, y}], inf);                
                }
            }
            else//t左 or s
            {
                if((y / 2) % 2)    add(i + n, t, inf);//如果有余数的话，说明是t左
                else//不然就是s
                    if(m[(point){x, y - 1}]) add(i + n, m[(point){x, y - 1}], inf);
            }//注意加了n才是出发点
        }
    }
}

void bfs()
{
    int x, now;
    c[t] = 1, x = t, q[++tail] = t;
    while(head < tail)
    {
        x = q[++head];
        for(R i=Head[x]; i; i=Next[i])
        {
            now = date[i];
            if(haveflow[i^1] && !c[now])
            {
                ++have[c[now] = c[x] + 1];
                q[++tail] = now;
            }
        }
    } 
    memcpy(good, Head, sizeof(Head));
}

inline void aru()
{
    while(x != s)
    {
        haveflow[last[x]] -= addflow;
        haveflow[last[x] ^ 1] += addflow;
        x = date[last[x] ^ 1];
    }
    ans += addflow;
}

void isap()
{
    int now; bool done;
    addflow = inf, x = s;
    while(c[s] != 200051)
    {
        if(x == t) aru(), addflow = inf;
        done = false;
        for(R i =good[x]; i ;i =Next[i])
        {
            now = date[i];
            if(haveflow[i] && c[now] == c[x] -1)
            {
                addflow = min(addflow, haveflow[i]);
                last[now] = i;
                good[x] = i;
                done = true;
                x = now;
                break;
            }
        }
        if(!done)
        {
            int go = 200050;
            for(R i=Head[x]; i ;i=Next[i])
            {
                now = date[i]; 
                if(haveflow[i] && c[now]) go = min(go, c[now]);
            }
            good[x] = Head[x];
            if(!(--have[c[x]])) break;
            ++have[c[x] = go + 1];
            if(x != s) x = date[last[x] ^ 1];
        }
    }
    printf("%d\n", ans);
}

int main()
{
//    freopen("in.in","r",stdin);
    fread(READ, 1, 7000000, stdin);
    pre();
    build();
    bfs();
    isap();
//    fclose(stdin);
    return 0;
}