算法学习——最小树形图
,,,本来只是想安静的做道题,,,结果是道最小树形图?
只好学习最小树形图了。
我们先来了解一下定义:
现在有一个有向图G(V,E),它具有如下性质:
1,没有环。
2,存在一个点x,它没有入度,且对于其他的点,有且只有一个入度。
此时x为树形图G的root
简单来说最小树形图就是给你一张图,让你找个树把图联通,让总权值最小
或者说最小树形图其实就相当于有向版的最小生成树
那么如何求呢?
我们可以采用朱刘算法。
我们需要先找到每个点的权值最小的入边,但这样可能有环or不联通,所以我们要去环,还要把图联通,
以下为主要算法流程:(不考虑缩点后的展开)
1,确定一个根
2,找到除根外每一个点的最小入边,若这些边构成了环(此时必然不联通),则缩环成点,并将环内的每一个点的其他入边都减去环内的入边,
3,重复步骤2直到没有环出现(构成了树)。
注意这是一个类似递归的过程,每次缩完点之后的点与其他点构成新图,不必考虑图是什么样的,我们只需要得到权值。这也是我之前陷入的一个误区。也就是说应当把缩完的点当做一个新点(正常的新点,不要和别的点分开,,,我们要平等的对待每一个点!)
为什么这样是对的呢?
我们观察缩点的过程,因为环的存在,图变得不联通,这时我们需要连上一条新边,例如:
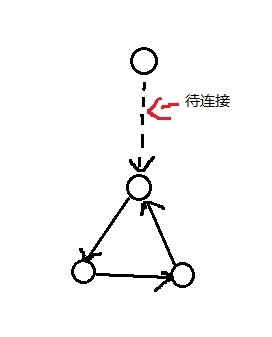
一旦我们连上这条新边,这将意味着我们要放弃一条环内的边,显然树要求不能有2个父亲,因此我们要删去入边,但这并不好操作,
于是注意到我们的目标仅仅是权值,因此我们将每个点在环外入边的权值减去环内入边的权值,所以当我们连上一条新边时,
这样操作的实际效果在权值上和删去环内入边是等效的,只是减的地方不同而已,反正我们是求和对吧
放2道板子题吧(虽然是一模一样的两道题,,,,)
[JSOI2008]小店购物 & bzoj4349:最小树形图 最小树形图
参考blog:


