[HNOI2009]最小圈
题解:
0/1分数规划的题。
不知道0/1分数规划的可以先看看我的简单介绍: 0/1分数规划
具体的还是来看题目吧。
这个题面应该还是比较直白的,
就是每条边有a[i]=权值,b[i]=1
求 的最小值,
的最小值,
其中选择的边必须构成一个环
所以我们修改权值为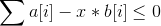 的左半部分
的左半部分
然后用spfa判负环即可
1 #include<bits/stdc++.h> 2 using namespace std; 3 #define R register int 4 #define AC 3100 5 #define ACway 11000 6 #define eps 1e-9 7 int n,m; 8 int date[ACway],Next[ACway],Head[AC],tot; 9 double mid,maxn,minn; 10 double length[ACway],Size[ACway],dis[AC]; 11 bool vis[AC],flag; 12 /*01分数规划emmm。。。 13 相当于代价为0了, 14 二分答案,然后将边权统一降低mid,因为是<=0,所以直接找负环就可以了*/ 15 16 inline int read() 17 { 18 int x=0;char c=getchar(); 19 while(c > '9' || c < '0') c=getchar(); 20 while(c >= '0' && c <='9') x=x*10+c-'0',c=getchar(); 21 return x; 22 } 23 24 inline void add(int f,int w,double S) 25 { 26 date[++tot]=w,Next[tot]=Head[f],Head[f]=tot,length[tot]=S; 27 } 28 29 inline void upmax(double &a,double b) 30 { 31 if(b > a) a = b; 32 } 33 34 inline void upmin(double &a,double b) 35 { 36 if(b < a) a = b; 37 } 38 39 void pre() 40 { 41 int a,b;double c; 42 n=read() , m=read(); 43 maxn = -INT_MAX,minn = INT_MAX; 44 for(R i=1;i<=m;i++) 45 { 46 a=read(),b=read(),scanf("%lf",&c); 47 add(a,b,c); 48 upmax(maxn,c); 49 upmin(minn,c); 50 } 51 } 52 53 void spfa(int x)//dfs版spfa判负环 54 { 55 int now; 56 vis[x]=true; 57 for(R i=Head[x]; i ;i=Next[i]) 58 { 59 now=date[i]; 60 if(dis[now] > dis[x] + Size[i]) 61 { 62 if(vis[now]) 63 { 64 flag = true; 65 break;//如果是return 的话就没办法回溯了,那样就会误判 66 } 67 dis[now] = dis[x] + Size[i]; 68 spfa(now); 69 } 70 if(flag) break;//也许可以剪枝???? 71 } 72 vis[x]=false; 73 } 74 75 void init()//重置边权 76 { 77 flag=false; 78 for(R i=1;i<=tot;i++) 79 Size[i] = length[i] - mid;//边权修改为真实权值 - 当前答案 80 memset(dis,0,sizeof(dis)); 81 memset(vis,0,sizeof(vis)); 82 } 83 84 void half() 85 { 86 double l=minn,r=maxn; 87 while(r - l > eps) 88 { 89 mid=(l + r) / 2.0; 90 init(); 91 for(R i=1;i<=n;i++) 92 { 93 if(flag) break; 94 spfa(i); 95 } 96 if(flag) r = mid; 97 else l = mid + eps; 98 } 99 printf("%.8lf\n",l); 100 } 101 102 int main() 103 { 104 // freopen("in.in","r",stdin); 105 pre(); 106 half(); 107 // fclose(stdin); 108 return 0; 109 }



