网络流
网络流
定义
1,网络流
用类似水流的定义,可以把一张图视作一堆管道,从s源源不断的流水,看最多有多少水可以汇聚到t (此处的水大致可以视作是每秒一定宽度的管道流过多少水之类的。)。
2,最大流最小割定理。
显然如果不把所有可以流的边都堵死就不能算一个最小割,因为还有可以到的边。
或者说最大流会在一组可以割的边中选最小的那个割掉,因为一组边可以流过的水显然是受容量最小的边所限制的。
3,必须流和可行流
1,最小割可行边,
意思就是最小割中可能出现的边。
充要条件:
1,满流
2,在残余网络中找不到x ---> y的路径
解释:
如果在残余网络中还找得到x--->y的路径的话,要割掉这条边就还需要割掉另一条路径,这显然是不够优的。如果是满流的话显然不是割掉了这条边
2,最小割必须边
1,满流
2,在残余网络中s 可以到 x, y 可以到 t。
解释:
满流的原因和上面原因一样,同时必须边肯定也是可行边(显然可行边的范围就要大一些嘛)。如果满流但s不能到x or y 不能到 t,因为这样的话说明在s 到 x(y 到 t)的路上就已经被割掉了,而不是在这里割的。但是因为满流了,所以这是可行的,但是由于割在别的地方,说明不是必须的。
因此s 必须可以到 x, y 必须可以到s才能保证是必须边,而不是可行边
至于实现方法就比较妙了,如果两个点在一个scc中则表示可以到,因此可行边需要保证x和y不在一个scc中,而必须边则还需要额外保证s 和 x 属于一个scc, y 和 t属于一个scc。
模板
这里只放非递归版ISAP。虽然看上去比较长,但好写好调。如果要学习原理的话需要百度?
----update in 2021/9/20---- 近期会更新一下isap的大概理解,应该可以帮助记忆代码吧。
稍微熟练一点的话,写起来还是比较快的,十多分钟吧。
#include<bits/stdc++.h>
using namespace std;
#define R register int
#define LL long long
#define AC 10100
#define ac 201000
const int inf = 1e9;
int n, m, x, s, t, all, addflow, head, tail, ans;
int Head[AC], date[ac], Next[ac], haveflow[ac], tot = 1;
int have[AC], good[AC], q[AC], c[AC], last[AC];
inline int read()
{
int x = 0;char c = getchar();
while(c > '9' || c < '0') c = getchar();
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x;
}
inline void upmin(int &a, int b) {if(b < a) a = b;}
inline void upmax(int &a, int b) {if(b > a) a = b;}
inline void add(int f, int w, int S)
{
date[++ tot] = w, Next[tot] = Head[f], Head[f] = tot, haveflow[tot] = S;
date[++ tot] = f, Next[tot] = Head[w], Head[w] = tot, haveflow[tot] = 0;
}
void bfs()
{
q[++ tail] = t, c[t] = have[1] = 1;
while(head < tail)
{
int x = q[++ head];
for(R i = Head[x]; i; i = Next[i])
if(!c[date[i]] && haveflow[i ^ 1])
have[c[date[i]] = c[x] + 1] ++, q[++ tail] = date[i];
}
memcpy(good, Head, sizeof(Head));
}
void aru()
{
while(x != s)
{
haveflow[last[x]] -= addflow;
haveflow[last[x] ^ 1] += addflow;
x = date[last[x] ^ 1];
}
ans += addflow, addflow = inf;
}
void isap()
{
bool done;
x = s, addflow = inf;
while(c[s] != all + 1)
{
if(x == t) aru();
done = false;
for(R &i = good[x]; i; i = Next[i])
{
int now = date[i];
if(c[now] == c[x] - 1 && haveflow[i])
{
upmin(addflow, haveflow[i]), last[now] = i;
done = true, x = now; break;
}
}
if(!done)
{
int go = all;
for(R i = Head[x]; i; i = Next[i])
if(c[date[i]] && haveflow[i]) upmin(go, c[date[i]]);
if(!(--have[c[x]])) break;
have[c[x] = go + 1] ++, good[x] = Head[x];
if(x != s) x = date[last[x] ^ 1];
}
}
}
void pre()
{
n = read(), m = read(), s = read(), t = read(), all = n + 3;
for(R i = 1; i <= m; i ++)
{
int x = read(), y = read(), z = read();
add(x, y, z);
}
}
int main()
{
// freopen("in.in", "r", stdin);
pre();
bfs();
isap();
printf("%d\n", ans);
// fclose(stdin);
return 0;
}
常见建模
1,最小路径覆盖
定义:用最少的链覆盖全图。
建图:将每个点分别拆成2个点,一个为出点,一个为入点,建立源点和汇点,分别连接s ---> 出点,入点 ---> t,容量为1,对于图中的每一条边,连出点 ---> 入点。ans = 点数 - 最大流
理解:这是一个二分图匹配问题,匹配2个点相当于合并2条路径,所以合并路径越多越优。
2,最小点覆盖 && 最大独立集
定义:
在一个二分图中,有如下定义:
- 最小点覆盖:选出一个点集使得所有边都被覆盖,同时使得点权之和最小;
- 最大独立集:选出一个点集使得没有边2个点都被覆盖,且点权之和最大。
结论:最小点覆盖 + 最大独立集 = 总点集
因为在最小点覆盖中,所有边都被覆盖了,所以取反之后,每条边最多只会选一个端点,因此是一个独立集。
又由于是最小的点覆盖,所以取反后的独立集也是最大的独立集。
因此我们给这个二分图增加源汇,然后直接跑最大流。
就是连:
- s ---> 奇点 : 点权
- 偶点 ---> t :点权
- x ---> y : inf
于是最大流就保证了每条边肯定都被覆盖了。
同时因为最大流 = 最小割,所以求出的是最小点覆盖。
那么如果要求最大独立集的话,用总点数减一减就可以了。
3,最大权闭合子图
定义:每个点有点权,要求选出一些点,满足这些点的出边连向的点也必须被选且点权之和最大。
建图:S向正权点连容量为权值的边,从负权边向t连容量为|权值|的边,对于原图上的边,在图上连容量为inf的边。答案即为:正权值之和 - 最大流
理解:可以看做先选了所有的点,然后如果割左边的边就是放弃选某些正权点,如果割右边的边就是选某些正权点然后承受相应代价。
4,带上下界网络流
1,无源汇带上下界可行流。
定义一个数组d[x]表示图中点x的入度下限和-出度下限和。
建图方式为:
对于图中每一条边,都连流量为上界-下界的边,并在加边的时候统计d[x]。
对于任意一个点,如果它的d[x] > 0,那么连s --- > x, 流量为d[x];
如果它的d[x] < 0, 那么连x --- > t, 流量为-d[x]。
然后直接从s到t跑网络流即可,如果满流即为合法,否则不合法。
如何理解?
因为下界是必须达到的,因此先把所有的边都强行达到下界。
在强行让所有边都达到下界后建出的图不能保证进入流量 = 流出流量,因为我们建图的时候,实际上将多余or少的流量给忽略了,因此我们要再加一些边表示这些被忽略的流量。
对于任意一个点,如果d[x] > 0,那么表示进来的流量有剩余,还没有流完,但此时图中并没有体现。因此从s给它补充d[x]的流量, 表示x还需要引进额外的d[x]流量。
反之,如果d[x] < 0,那么表示进来的流量不够用,除此之外还需要额外流出去-d[x]的流量,但此时图中并没有体现。所以向t连边表示点x还需要向t输出-d[x]的流量。
如果满流,那么代表剩余的流量可以恰好补全不够的流量,那么就是可行了。
同时因为每条边都变为了上界-下界,因此不管怎么流,都是不会超过上界的,于是就成功的把流量限制在了[下界,上界].
2,有源汇带上下界可行流。
建图方式与上述相同,只是把原来的源汇连一条t --- > s : inf的边(现在的超级源汇为ss, tt)
3,有源汇带上下界最大流。
先做一遍可行流,然后去掉ss和tt,在残余网络上跑最大流,最大流即为答案。
因为有反向边,所以之前可行流流出的流量会从反向边流到t,于是基础流量就会被满足了,然后就是在这个基础上增添流量。
又因为是最大流,所以跑出来的肯定是最优解。
4,有源汇带上下界费用流
建图方式和网络流差不多,原图上的边费用不变,新增的边费用为0.一开始减掉下界的时候要加上流下界的费用。
最后和跑出的费用相加,得到最后的费用。
5,切糕模型
问题:给定一个\(n \times m\)的矩阵,给每个位置填上一个\([1, k]\)之间的数,位置\((i, j)\)填\(t\)可以得到\(v(i, j, t)\)的代价。方案合法当且仅当每个位置的数与相邻的四个位置的数相差不超过\(d\).求一个最小总代价。
建图:先忽略相差不超过\(d\)的限制,考虑这样建图:
对于每个位置,拆成\(k\)个点。
- s ---> (i, j, 1) : v(i, j, 1)
- (i, j, t - 1) ---> (i, j, t) : v(i, j, t)
- (i, j, k) ---> t : inf
于是割掉(i, j, t) ---> (i, j, t + 1)的边就相当于这个位置填\(t\).
再考虑如果限制\(d\)。
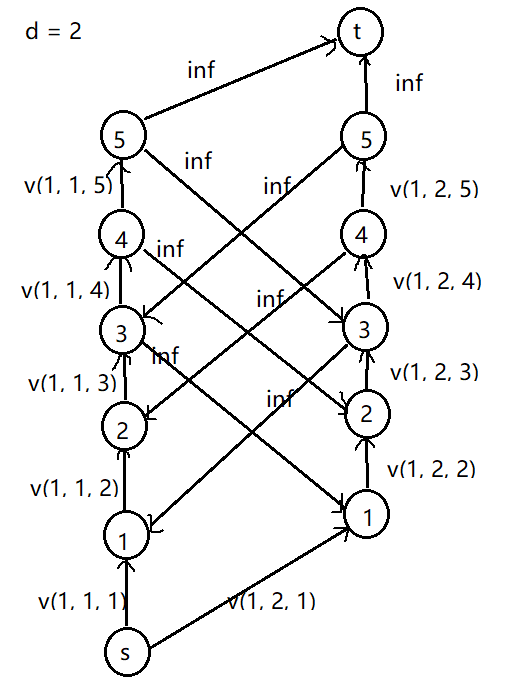
----update in 2021/9/19----不知道为什么这幅图不能正常显示,,,找个机会修修吧
来分析一下这幅图:
- 对于一个左边的点\(x\),如果右边取的边比它小\(2\)以上的话,因为\(inf\)是割不掉的,因此还会有流量通过这条边将\(\ge x - 2\)的边充满,也就相当于取走了上面的边。
- 对于一个左边的点\(x\),如果右边取的边比它大\(2\)以上的话,假设右边取走了\(y \ (y - x > 2)\),那么相对于\(y\)而言,就相当于左边取走了一个比它小\(2\)以上的边,与上一种情况冲突,所以不会出现。(这两种情况实际上是站在不同的点上看同一种情况)
因此这个建图就合法了。



