计算几何
向量
向量相关的一些基本量计算
向量的模:\(|\vec{AB}| = \sqrt{(x^2 + y^2)}\)
向量的简单表示:\(\vec{AB} = (x2 - x1, y2 - y1) = (x, y)\)
点积
公式
特别的,如果2个相同向量相乘:
扩展
那么我们可以利用这个式子来计算2个向量之间的夹角。
同时,由上式可以看出,点积的正负由夹角决定,即:
- 当\(\theta < 90^\circ\)时,点积为正
- 当\(\theta = 90^\circ\)时,点积为0,2个向量互相垂直
- 当\(\theta > 90^\circ\)时,点积为负
\(\Delta\):点积满足交换律。
叉积
公式
扩展
\(\vec{v} \times \vec{u}\)恰好等于这2个向量组成的三角形的有向面积的2倍。
所以2个向量组成的三角形面积为:\(\frac{\vec{v} \times \vec{u}}{2}\)
叉积的正负由向量的位置关系所决定。
- 当\(\vec{y}\)在\(\vec{x}\)左边时,\(\vec{x} \times \vec{y}\)为正
- 当\(\vec{y}\)在\(\vec{x}\)右边时,\(\vec{x} \times \vec{y}\)为负
- 如果\(\vec{y}\)与\(\vec{x}\)方向相同时,\(\vec{x} \times \vec{y}\)为零
即如下图所示:
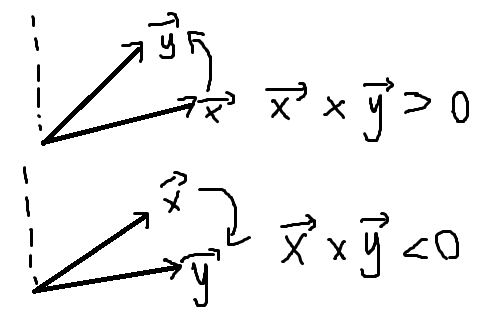
(当然判断方向的时候要用角度小的那边,用顺时针还是逆时针方向来判断)
由此可见,叉积没有交换律。同时叉积也由于这个性质,常在维护凸包的过程中被使用。
凸包
极角排序
其实也不知道这个是不是,,,就是这样:
bool cmp(node a, node b)
{return (a.x != b.x) ? a.x < b.x : a.y < b.y;}
叉积维护
极角排序后,依次遍历每个点,假设上2个点是\(p_0\)和 \(p_1\),新加入的点是\(p_2\),那么要根据\(\vec{p_0p_1} \times \vec{p_1p_2}\)的值来判断。
动态凸包
Splay
在插入一个点的时候,先找到如果可以放入凸包,那么应该放在哪里。
然后在找前驱后继,如果比前驱后继优秀,那么就弹出前驱后继。
重复以上过程,最后合并的时候可能细节比较多(判断这个点是否应该加入凸包等等)。
因为每个点只会被删除一次,每次弹到不能弹就停下了,所以插入的总复杂度是\(O(nlogn)\)
但是如果询问的\(k\)不单调的话,就需要二分相切的点,然后再在splay上二分的查询,所以复杂度就\(O(nlog^2n)\)的了
缺点:
- 代码长,细节多
- 可能会常数大?
- 查询复杂度\(log^2\)
优点:
- 在线做法
- 比较无脑
CDQ维护凸包
先按照\(k\)排序,然后在\(cdq\)的时候左边按\(x\)排序,右边按\(k\)排序。
相当于先打乱,再最后排成\(x\)升序的序列。
这样的话,用左边的来更新右边的,因为左边\(x\)升序,右边\(k\)升序,所以就相当于是二者都单调了。
因此注意要先处理完左边对右边的贡献,再递归右边区间。
然后再把整个区间按照\(x\)排序,这样才可以保证在处理贡献的时候始终单调。
注意到把整个区间按照\(x\)排序的时候已经把右侧的也递归处理完了,所以右边现在也是\(x\)升序的了,于是直接归并合并就好了。
此外因为在一个区间没有全部处理完之前,\(k\)升序的条件都是要用的,所以右区间再分小区间的时候,也要保证分出来的小区间中右区间是单调的.当然因为这里是\(cdq\),所以先递归左边,最后递归右边就可以保证在中间进行计算的时候两边都合法了。
缺点:
- 只能离线
优点:
- 代码短,相对来说好写
- 不管询问的斜率是否单调,总复杂度都是\(O(nlogn)\)的
#include<bits/stdc++.h>
using namespace std;
#define R register int
#define inf 1e9
#define eps 1e-9
#define AC 100400
int n;
int q[AC];
double f[AC];
struct day{
double k,x,y,a,b,r;int id;
}t[AC],m[AC];
inline bool cmp(day a,day b)
{
return a.k < b.k;
}
inline double getk(int i,int j)
{
if(fabs(t[i].x - t[j].x) <= eps) return inf;
return (t[j].y - t[i].y) / (t[j].x - t[i].x);
}
void pre()
{
scanf("%d%lf",&n,&f[0]);
for(R i=1;i<=n;i++)
{
scanf("%lf%lf%lf",&t[i].a,&t[i].b,&t[i].r);
t[i].k=-t[i].a / t[i].b,t[i].id=i;
}
sort(t+1,t+n+1,cmp);//先按照k排序,然后在cdq的时候左边按x排序,右边按k排序
}/*也就相当与先打乱,然后最后排成x升序的序列
这样的话,因为左边x升序,右边k升序,就相当于是单调的了,
然后注意先处理完左边对右边的贡献,然后再递归右边区间,
然后再把整个区间按照x排序,这样才可以保证在处理贡献时始终单调,
因为在一个区间没有全部处理完之前,k升序的条件都是要用的,
因为右区间再分小区间的时候也要保证分出来的小区间中右区间k升序*/
inline void merge(int l,int r)//按x递增排序
{
int mid=(l + r) >> 1,ll=l,rr=mid+1;
int tot=0;
/* for(R i=l;i<=mid;i++) printf("%.2lf ",t[i].x);
printf(" + ");
for(R i=mid+1;i<=r;i++) printf("%.2lf ",t[i].x);
printf("\n=");*/
while(ll <= mid && rr <= r)
{
if(t[ll].x < t[rr].x + eps) m[++tot]=t[ll++];
else m[++tot]=t[rr++];
}
while(ll <= mid) m[++tot]=t[ll++];//error!!!这里是while啊喂
for(R i=1;i<=tot;i++) t[l + i - 1]=m[i];
/* for(R i=l;i<=r;i++) printf("%.2lf ",t[i].x);
printf("\n\n");*/
}
void cdq(int l,int r)
{
if(l == r)
{
f[l]=max(f[l],f[l-1]);//每更新一次f就要更新x和y
t[l].y=f[l] / (t[l].a * t[l].r + t[l].b),t[l].x = t[l].y * t[l].r;
return ;
}
int mid=(l + r) >> 1,ll=l-1,rr=mid,top=0;
for(R i=l;i<=r;i++)
if(t[i].id <= mid) m[++ll]=t[i];
else m[++rr]=t[i];//要保证只能用前面的更新后面的(相当于是从k升序的序列里按顺序调了几个出来,
//放到左边,剩下的放右边,因为是按顺序拿的,并且本来就有序,所以拿出来后还是有序的
//相当于倒着归并
for(R i=l;i<=r;i++) t[i]=m[i];
cdq(l,mid);//要先处理完左边的,这样处理完后左边就x升序了
for(R i=l;i<=mid;i++)
{
while(top >= 2 && getk(q[top],i) + eps > getk(q[top-1],q[top])) --top;
q[++top]=i;
}
int be=mid+1;
for(R i=be;i<=r;i++)
{
while(top >= 2 && getk(q[top-1],q[top]) <= t[i].k + eps) --top;//...
int now=q[top];
f[t[i].id]=max(f[t[i].id],t[now].x * t[i].a + t[now].y * t[i].b);
}
cdq(mid+1,r),merge(l,r);
}
int main()
{
// freopen("in.in","r",stdin);
pre();
cdq(1,n);
printf("%.3lf\n",f[n]);
// fclose(stdin);
return 0;
}


