古典密码
替代密码
单表替代
每个字母对应的密文字母固定。
- 一般单表替代
密钥空间n = 26! - 移位密码
凯撒密码就是密钥为3的移位密码。 - 仿射密码
加密:k1*m + k0 (mod 26)
要求k1与26互素,避免出现多个明文对应同样的密文。 - 密钥短语密码
密钥是一个短语(单词),写在替代表最前端,整张替代表去掉所有重复字母。
多表替代
- 维吉尼亚密码
a-z用0-25编号,明文对应数字按位加上密钥(长度不够就循环使用)对应数字mod26,得到的数字译成字母就是密文。 - 希尔密码
密钥是一个n*n矩阵,将明文分为长度为n的组,密钥矩阵乘上每个分组矩阵,结果mod26得到密文对应矩阵,按原顺序拼成完整密文。 - 一次一密密码
难以做到。 - Playfair密码
基于一个5*5方格。
密钥去除重复字母按行从左上开始填入,具体类似于密钥短语密码填替换表的方法。i和j填在同一格。
明文两个分为一组。遵循下述复杂规则:
- 若两字母同行,分别加密为右侧紧邻字母。
- 若两字母同列,分别加密为下方紧邻字母。
- 若不同行不同列,分别加密为由两字母确定的矩形的同行字母。
- 若两字母相同,则在两字母中间插入一个事先约定的字母,按上述规则处理。
- 若明文长度为奇数,在末尾插入事先约定字母。
- 上下边界、左右边界进行循环。
置换密码
周期置换密码
给出一个置换密钥Π,按密钥长度将明文分组,每一组按照密钥进行置换后按顺序拼成密文。
列置换密码
给出一个置换密钥Π,明文按密钥长度为一行写出,按列执行密钥的置换。
转轮机密码
慢、中、快三个转子,慢端输入明文,快端输出密文。每次按键,快端向下移动一个位置,26次后中端移动,中端移动26次后慢端移动。加解密双方需要使用同样的转轮机。
分组密码
DES
算法描述
明文分组为64位,初始密钥64位,有效密钥56位,输出密文64位,16轮迭代的分组对称密码算法。基本操作是置换、替换、异或、循环移位。加解密算法相同,只是使用密钥的顺序相反。
流程图
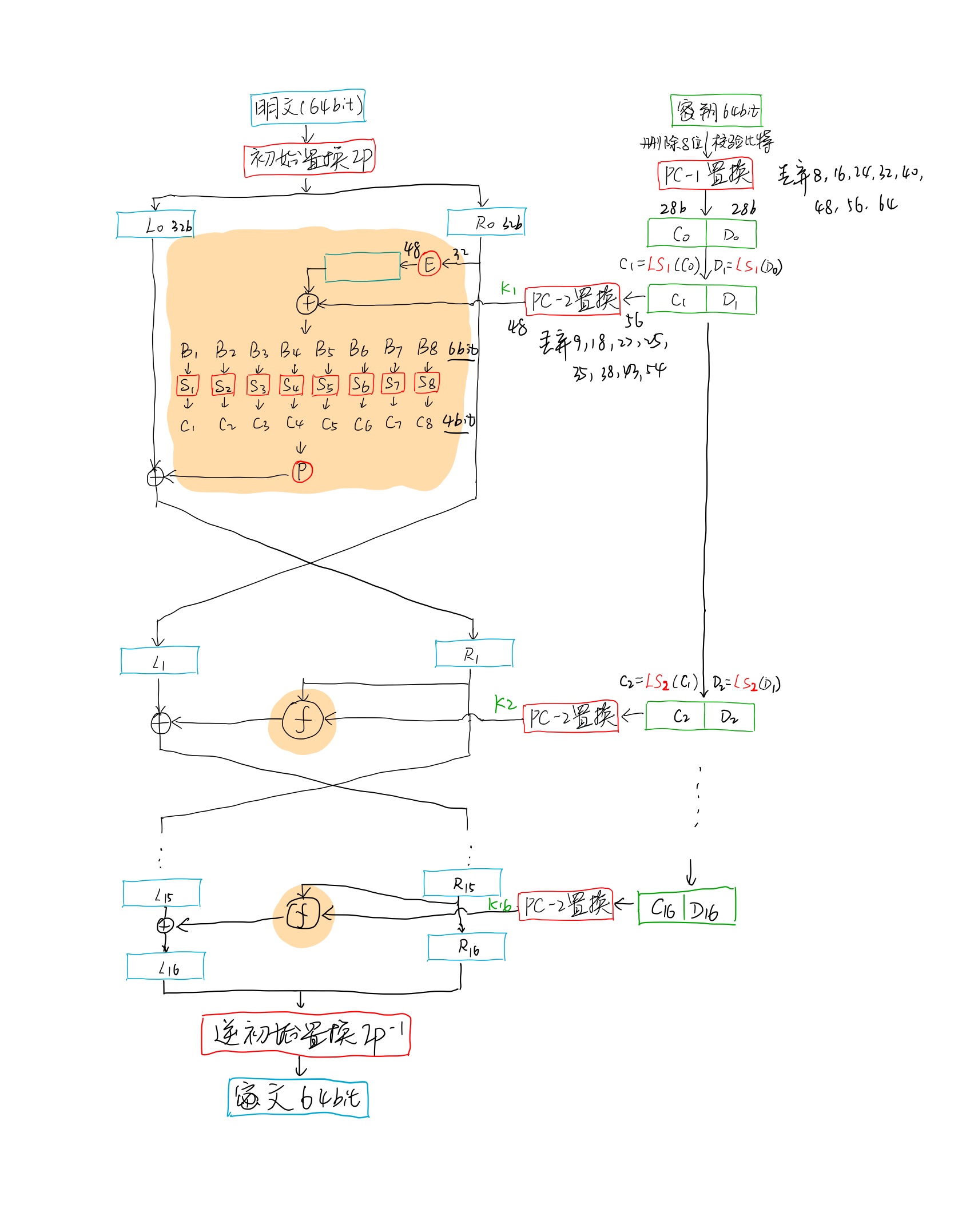
加密过程
密钥生成
-
64位初始密钥先进行一个PC-1置换,目的是根据置换表去掉8位奇偶校验位,并打乱剩下的56位有效密钥的顺序。将这56位分成C0和D0。
-
两部分分别根据LSi的值进行循环左移,左移后通过PC-2置换,然后合并作为48位子密钥。
-
整个des中一共会左移十六轮,第1、2、9、16次是左移一位,其他都是左移两位。
处理明文
-
初始置换IP
先对明文(64位)进行一个初始置换IP,将明文分为L0、R0两个32位块。
该过程并不会增加DES的安全性,但这种做法在16位和32位的总线出现之前将使得数据更容易加载到DES芯片中。 -
迭代
进行16轮Feistel加密。每一轮都用一个从初始密钥导出的48位且每次不同的密钥(密钥生成过程如上文所述)。
每一轮操作:
(1)E扩展置换
用E置换处理每一轮的R0。目的是把32位的R0扩展为48位,和密钥长度相同,以进行异或操作。
置换过程就是:针对4比特×8组,把每一组的第一位放在上一组的最后一位后面,把每一组的最后一位放在下一组的第一位前面。
置换之后的R与该轮密钥进行异或。
(2)S盒替换
把异或之后得到的48位送入通过8个内有不同替代表的S-盒,进行替代运算。每个S盒有6位输入4位输出,48位输入分为8个6比特的分组,一个分组对应一个S盒。每一个S盒中是4行16列的表,盒中的每一项都是一个4位的数。用6位输入的第一位和第六位确定所在行,中间四位确定列,对应一个格子里的值,即该组的替代运算结果。
(3)P盒置换
S盒代替运算的32位输出输入P盒进行置换。
(1)(2)(3)加起来构成f函数
(4)左右交换
P盒置换的结果与32位的L0异或,然后左、右半部分交换,开始下一轮。
注意第16轮中,最后一步不进行左右交换,直接把左右合并。 -
初始IP逆置换
第16轮结束后,左右合并的结果进行IP逆置换。最后得到密文。
算法分析
- S盒设计准则
输入改变1比特,至少2比特的输出会随之改变。 - 完全性
(1)完全性定义:任何一位输入的改变都能影响到每一位输出。
(2)如果Feistel的f函数的完全的,(最差情况下)Feistel需要3圈来实现完全性。
(3)如果Feistel的f函数需要T圈迭代来实现完全性,则Feistel需要T+2圈实现其完全性。
(4)DES经测试,经过5圈即可实现完全性,实际算法中进行16圈迭代是为了提高其安全性。
(5)DES有对称互补性,所以进行暴力攻击时只需要试验2^56个密钥的一半。
AES
算法描述
AES有128位的分组长度,密钥可以是128、192或256位。AES把一个字节看作有限域GF(2^8 )上的元素,生成有限域的不可约多项式是x^8 +x^4 +x^3 +x+1。AES使用的模数多项式是x^4 +1。
加密过程
- 明文初始化为State,并于轮密钥进行一次异或(AddRoundKey)。
- 前9轮:S盒替换(SubBytes)—— 行移位(ShiftRows)—— 列混淆(MixColumns)—— 异或(AddRoundKey)。
- 最后一轮:SubBytes——ShiftRows——AddRoundKey
- 最后输出的就是密文。
SubBytes
使用16个相同的S盒,将128bit分成16组。
是AES中唯一的非线性变换。
ShiftRows
第一行不动,第二、三、四行分别循环左移2、3、4个字节。
MixColumns
AES选取的固定多项式{03}x^3 +{01}x^2 +{01}x+{02}。State的每一列与这个多项式进行模x^4 +1的乘法。
列混合过程就是xtime过程.
- 如果b7 = 0,结果就是b6b5b4b3b2b1b00
- 如果b7 = 1,结果就是b6b5b4b3b2b1b00与00011011进行异或,这个00011011就是构成AES有限域的固定多项式去掉最高次项的结果。
AddRoundKey
轮密钥每一列与State的对应列进行异或。
AES解密可直接逆向进行加密过程实现。
解密过程优化
- SubBytes与ShiftRows顺序可换
- MixColums和InvMixColumns都是线性变换
所以:
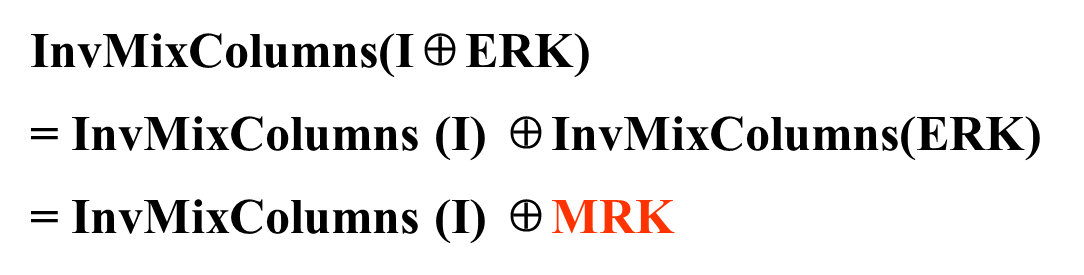
优化之后,可以实现加密过程与解密过程逻辑顺序相同,只是使用的密钥不同。如下图。
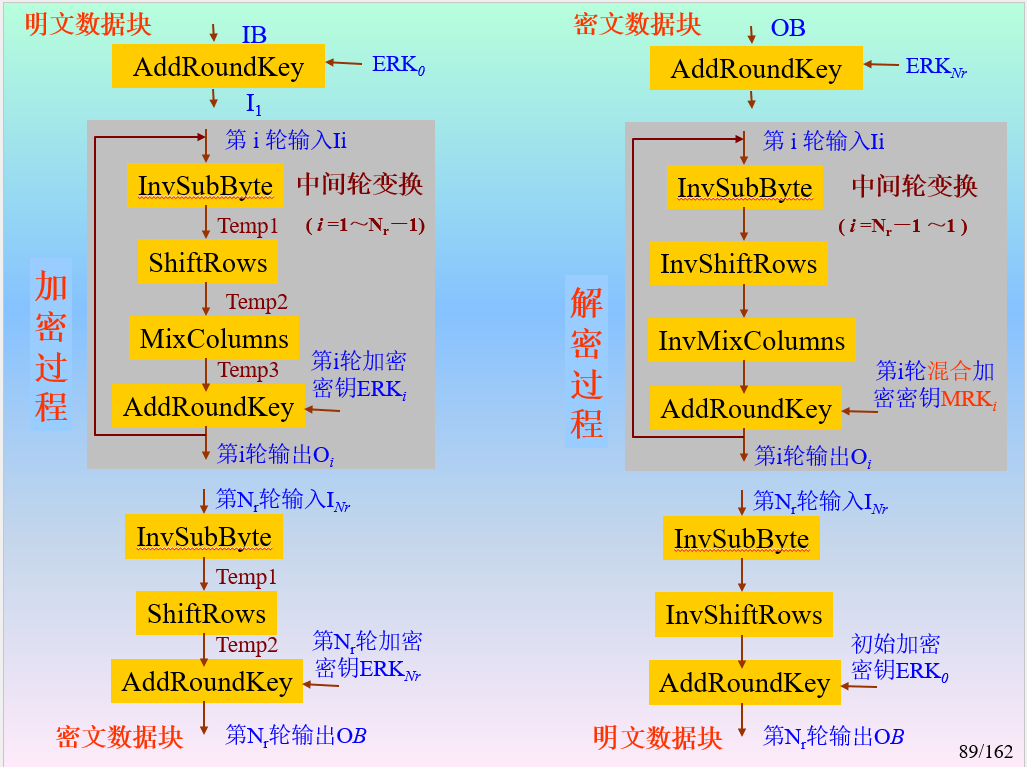
分组密码操作方式
- ECB电码本
大单表替换。 - CBC密码块链接
初始向量IV需要被当作密文传输。
有限传播:密文每一位的错误会影响当前轮和下一轮的解密。 - CFB密码反馈
分组密码 -> 流密码,可以实时加密。
密文中一位的错误最多会影响ceil(b/s)的解密。 - OFB输出反馈
内部反馈:同步流密码,通过反复加密IV得到密钥流。
没有错误传播,可以预计算。 - CTR计数器
每处理完一个分组后,计数器加上一个常数。 - CSM密文窃取
公钥密码
RSA
- 根据RSA计算原理,n必为奇数,φ(n)必为偶数,e和d都必为奇数。
- RSA是Zn -> Zn的一种单表代换密码,其安全的原理在于,当n极大时,只要不知道pq,根据陷门单向函数特性,很难通过密文推断出密钥或明文信息。且在同一个加密过程中,不同的明文一定对应不同的密文。
- 用中国剩余定理CRT可以加速RSA解密(因为需要知道p和q,所以只能辅助解密不能辅助加密)
- RSA安全问题
1)用户之间不能共享n
2)不同用户不能选择相同的密钥
3)同一个密钥不能同时用于加密和解密,可能面临选择密文攻击
ElGamal
安全性
基于有限域上离散对数问题的困难性。
具体描述
- 密钥生成
系统选一个大素数p,a是p的一个原根。随机生成一个整数x满足2 <= x <= p - 2,计算y = \(a^x\) mod p
(p,a,y)是公钥,x是用户的私钥。 - 加密
待加密的明文为m(m < p)
随机选一个整数k(2 <= k <= p - 2)
c1 = \(a^k\) mod p
c2 = m · \(y^k\) mod p
密文就是(c1,c2) - 解密
用私钥x对(c1,c2)进行解密
m = c2 · (\(c_1^x\))^-1 - p应至少有1024位,p-1应该具有一个较大的素因子
期末
密码的要求
机密性、数据完整性(对称(哈希、MAC)和非对称(数字签名))、鉴别、抗抵赖性(只有数字签名)
分组密码工作模式
- ECB电子密码本
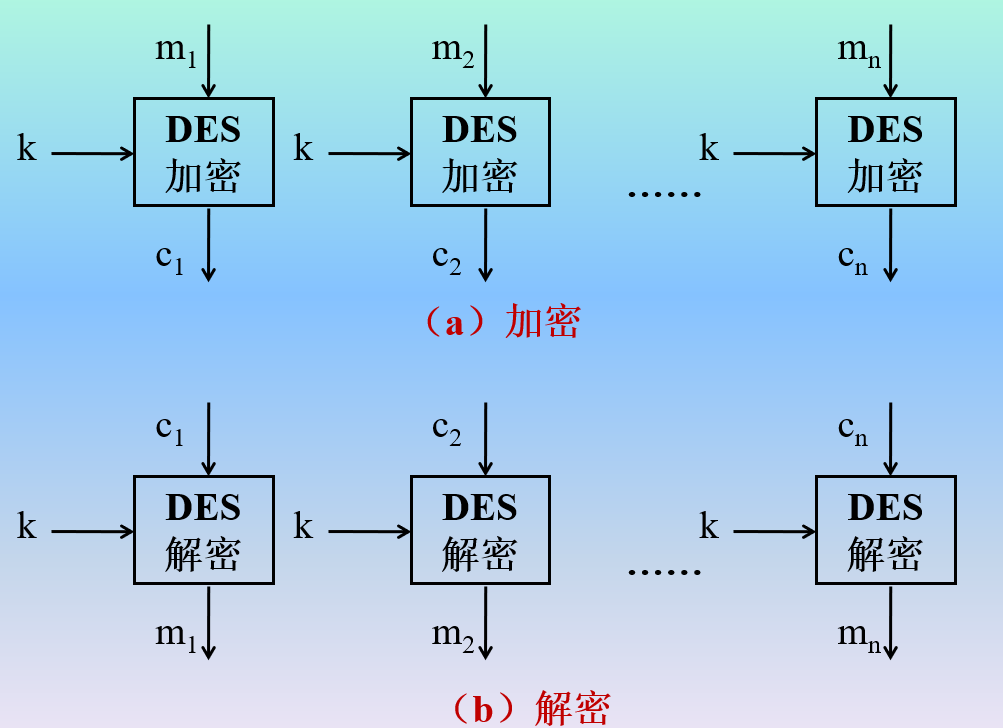
相同明文加密后产生相同密文;可能被敌手通过分组夹带方式攻击
无法纠正传输中的错误 - CBC密码分组链接
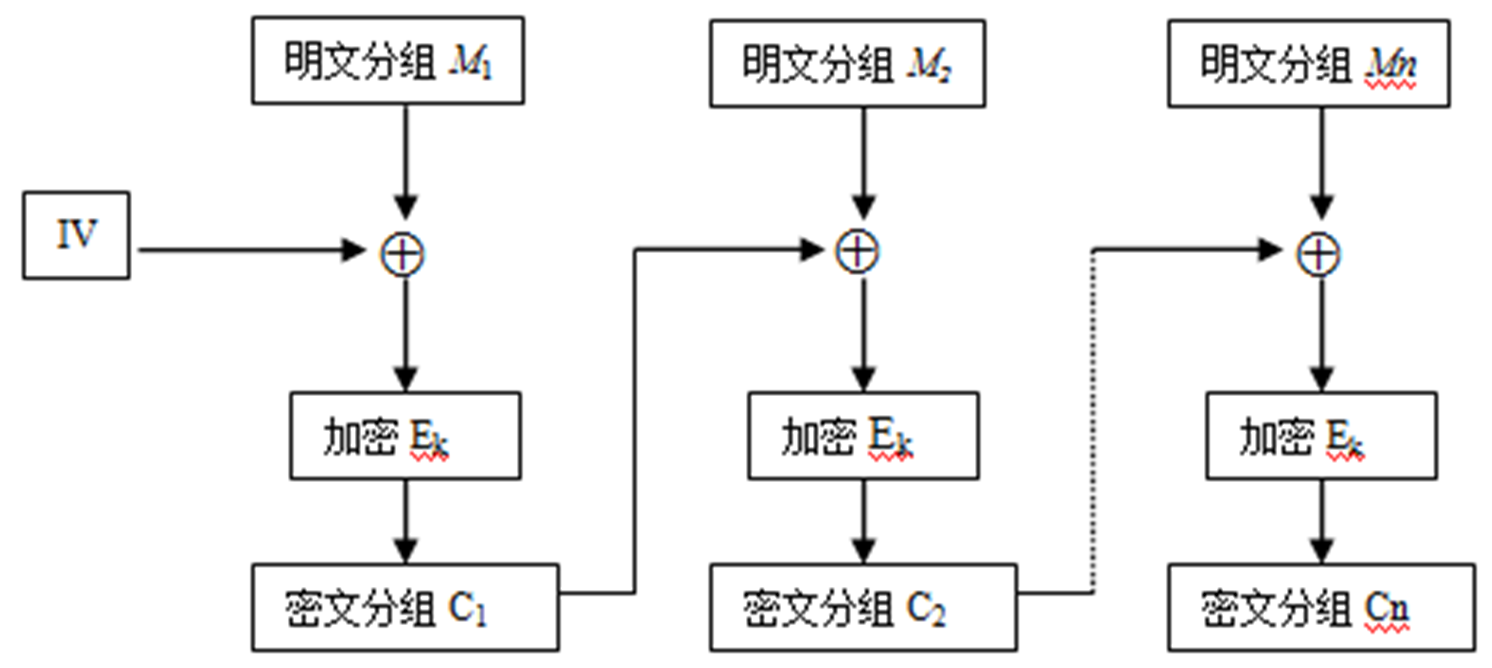
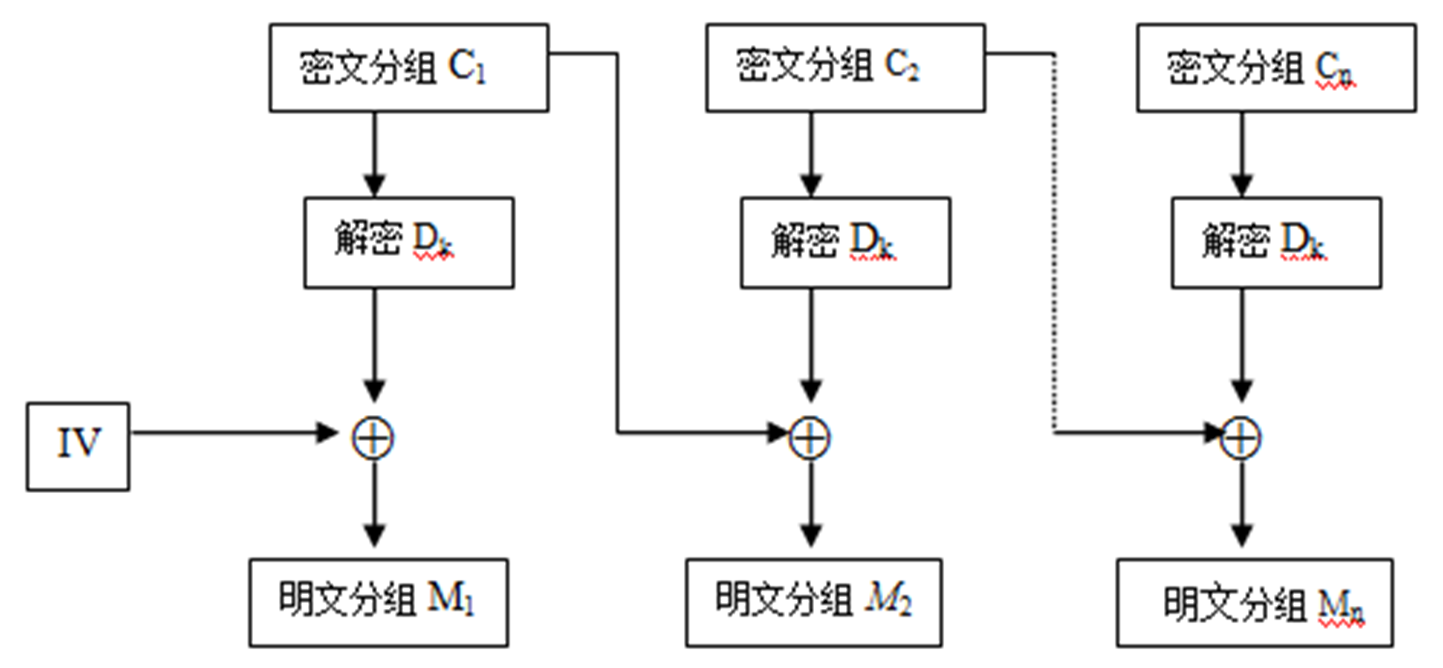
IV要被双方都知道,不用保密,需要随着消息进行更换
相同明文一般对应不同密文,能抵抗对分组的篡改(重放、插入、删除)
密文中一个位的错误会影响当前分组以及下一个分组的解密,自同步 - CFB密码反馈
分组密码转换为流密码
某个密文分组出现错误,会影响当前分组以及后面【最多】ceil(b/s)个分组的解密错误 - OFB输出反馈
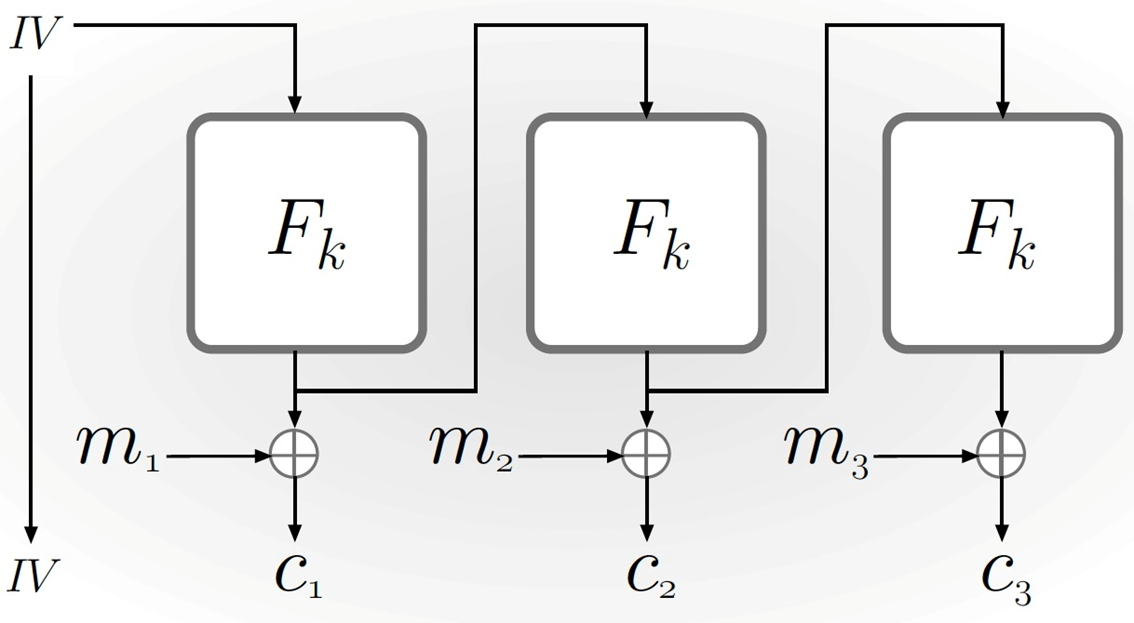
同步序列密码,通过反复加密一个IV得到密钥流,可以预计算
密钥相同的情况下,每次加密要使用不同的IV(OTP)
可加密任意长度的数据,没有错误传播
不能检测对密文的篡改 - CTR计数器
使用同一密钥时,相同明文产生不同的密文
可以随机对任意密文分组进行解密(每个密文的解密与其他密文块无关)
能并行对多个分组进行加解密处理
最主要的处理部分不依赖明密文,可以预计算
可以处理任意长度的数据,不需要实现解密算法(加解密都使用加密运算)
RSA安全问题
从公钥导出私钥理论上可行,计算上不可行
安全性依赖于大整数分解的困难性
- 小指数攻击
如果e很小,可以直接爆破e或者进行有限域开方 - 共享模数n
若两个用户用的是相同的n,则可以分解n - 选择密文攻击
加密和签名不能用同一对密钥
ElGamel安全问题
安全性依赖于有限域上计算离散对数的困难性
- k必须不可预测
- k重用
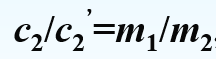
若两次加密使用相同的k,则只要知道一个明文,就可以算出另一个明文
ECC
优点:密钥比RSA短
安全性依赖于有限域上计算离散对数的困难性
消息鉴别
哈希本身没有密钥,所以不能直接用于消息鉴别;MAC是带有保密的密钥的哈希
基于对称分组密码的CBC工作模式的哈希(散列函数的设计方法之一):计算效率低,如果密钥保密,得到的是MAC(报文鉴别码)。密钥公开时,不能作为通常的不带密钥的哈希。因为只计算最后一个密文块的哈希,所以攻击者可以截取消息后通过构造,对消息进行篡改而不改变哈希值。
报文鉴别的实现方式:基于对称加密(差错控制,提供鉴别和机密性,不提供数字签名);基于公钥加密(可以提供鉴别、机密性和数字签名);基于散列函数(HMAC)
HMAC的安全性依赖于其中嵌入的散列函数的安全性
数字签名
- RSA签名
安全性取决于RSA加密算法的安全性(选择密文攻击,加密和签名不能用同样的密钥)
如果知道m1,m2及他们分别对应的签名s1和s2,则知道m1m2的签名就是s1s2
任何人都可以使用某人的公钥e来伪造对于随机消息的签名,但无法为选定的消息伪造签名 - ElGamal
安全性依赖于有限域上求解离散对数问题的困难性
非确定的签名(随机性)
如果随机数k泄露,敌手可以算出签名者私钥;
如果重用k,敌手可以根据两个不同消息的签名算出签名者私钥 - DSA
散列函数用的是SHA-1
只能签名,不能用于加解密(因为私钥不能解密使用公钥加密的数据)
安全性依赖于有限域上求解离散对数问题的困难性
是ElGamal的改进签名算法,非确定的
如果重用k,则可以用两个不同的签名计算出k和签名者私钥
线性k攻击:如果用不同的k1,k2对m1和m2分别签名,但k2 = a·k1 + b,也可以通过两个不同的签名求出签名者私钥 - ECDSA
是DSA在椭圆曲线上的模拟,安全性依赖于椭圆曲线上秋决离散对数的困难性
如果重用k,则可以用两个不同的签名计算出k和签名者私钥 - 特殊场景签名
1)不可否认签名
只有签名者参加的情况下才能验证签名,且签名者不能否认签名(签名;验证;否认)
2)盲签名
需要某人对某数据签名,且不让其知道数据的具体内容。(加密和签名)
在需要实现某些参加者匿名性的密码协议中应用。消息内容对签名者不可见,且签名被公开后,签名者不能追踪签名。
3)群签名
只有群中成员可以产生有效签名;验证者能验证签名有效且来自该群组,无法定位到个人;发生争议时借助可信机构或者群成员联合可以识别出签名者。
匿名性、不关联性、防伪造性、可跟踪性、可开脱性(不能以他人的名义产生有效群签名)、抗合谋攻击,不支持撤销
密钥管理
密钥协商 Diffie-Hellman
攻击目的:在攻击者与正常通信的一方之间建立起一个“安全”密钥
安全性基于有限域上计算离散对数的困难性
没有身份鉴别,易受中间人攻击,中间人与通信双方之间分别形成密钥,以截获两人发的消息且不被发现
Shamir秘密分割
基于多项式的拉格朗日插值公式
是完善的门限方案,是无条件安全的;易于扩充新用户;门限值固定;秘密分发者知道参与者的个数;不能防止秘密分发者和参与者的欺诈(合谋)
身份鉴别
抵御重放攻击的基本方法:时间戳(但是需要双方同步);质询/响应(每次通信要附加一些内容);挑战/应答(与前者类似,每次通信时验证者向声称者发送一个挑战字串,声称者需要按双方商量好的方式进行应答)
注意双向鉴别不是必须达到的要求
鉴别方法
所知;所有;不可改变的特性;零知识证明
S/Key一次性口令身份鉴别
可以防止重放(口令不可重复使用),不能防止小数攻击
用户与鉴别服务器之间传输的信息只是口令信息的散列值
缺乏完整性保护机制,不能保护鉴别过程中受到的主动攻击(注入虚假信息、修改口令、修改鉴别数据等)
序列密码
对称密码,与分组密码的最大区别是序列密码是有记忆的
分为同步(密钥流与明密文无关,无错误传播,要求双方同步)和自同步(假设密钥序列产生器有n位,则一位的错误会影响到后面n位的解密,即有限错误传播;自同步,只要连续收到n个正确的明文,双方的密钥序列产生器就会自动恢复同步)
线性反馈移位寄存器LFSR
不能直接用于产生密钥序列(因为周期太小),适合硬件实现
m序列在一个周期内,0和1出现的次数分别是\(2^{n-1}-1\)和\(2^{n-1}\)
RC4
安全性不高,以随机置换为基础、可变密钥长度、面向字节操作,基于非线性数据表变换
分为状态表初始化(密钥调度算法KSA)和密钥流生成(伪随机序列生成算法PRGA)
大多数攻击在理论上都是可行的,但是计算上是不可行的
单表替代:一般单表替代;移位;仿射;密钥短语
多表替代:维吉尼亚;希尔;一次一密;playfair
置换:周期置换;列置换
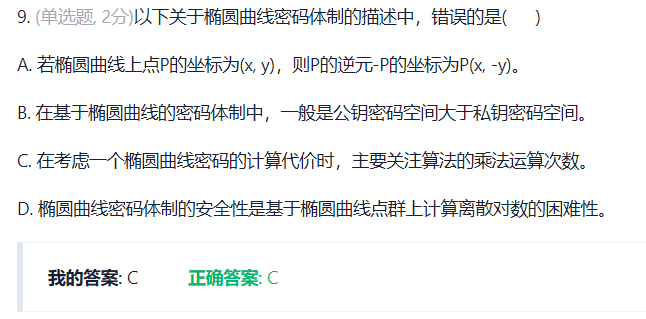
这个“大素数分解” 大素数如何分解??

应该是等于O




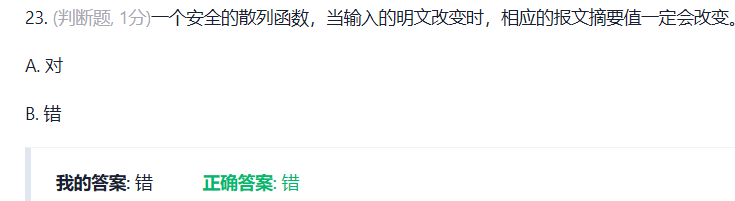
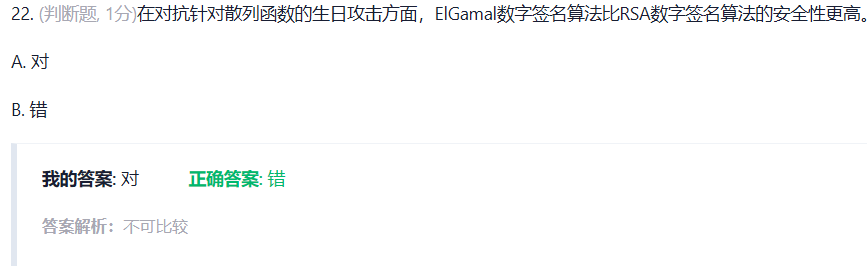
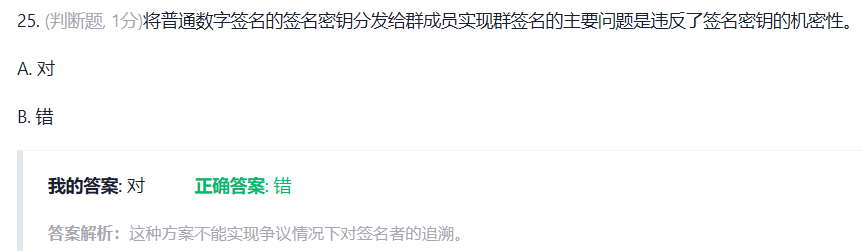
群签名,成员的密钥确实需要保密
字典攻击和暴力攻击不同,加扰只是让得到字典的过程变难了,暴力攻击就是一个个尝试,加不加扰对他没影响


 浙公网安备 33010602011771号
浙公网安备 33010602011771号