简单回顾一下深度优先搜索和广度优先搜索

一、先了解定义

深度优先搜索

深度优先搜索属于图算法的一种，是一个针对图和树的遍历算法，英文缩写为DFS即Depth First Search。深度优先搜索是图论中的经典算法，利用深度优先搜索算法可以产生目标图的相应拓扑排序表，利用拓扑排序表可以方便的解决很多相关的图论问题，如最大路径问题等等。一般用堆数据结构来辅助实现DFS算法。其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。

广度优先搜索

广度优先搜索（也称宽度优先搜索，缩写BFS，以下采用广度来描述）是连通图的一种遍历算法这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS，属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。基本过程，BFS是从根节点开始，沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问，则算法中止。一般用队列数据结构来辅助实现BFS算法。

 

二、上笔记图

 

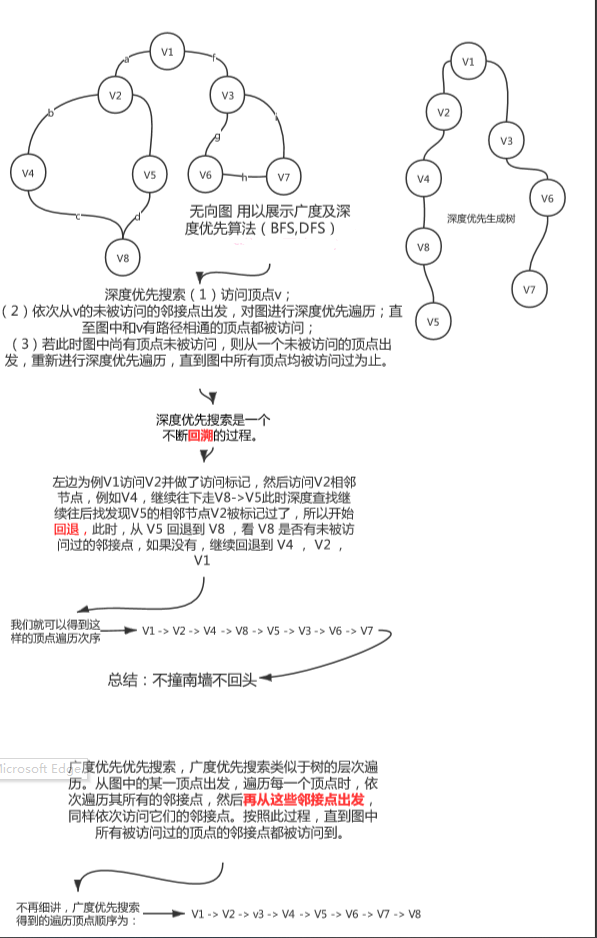
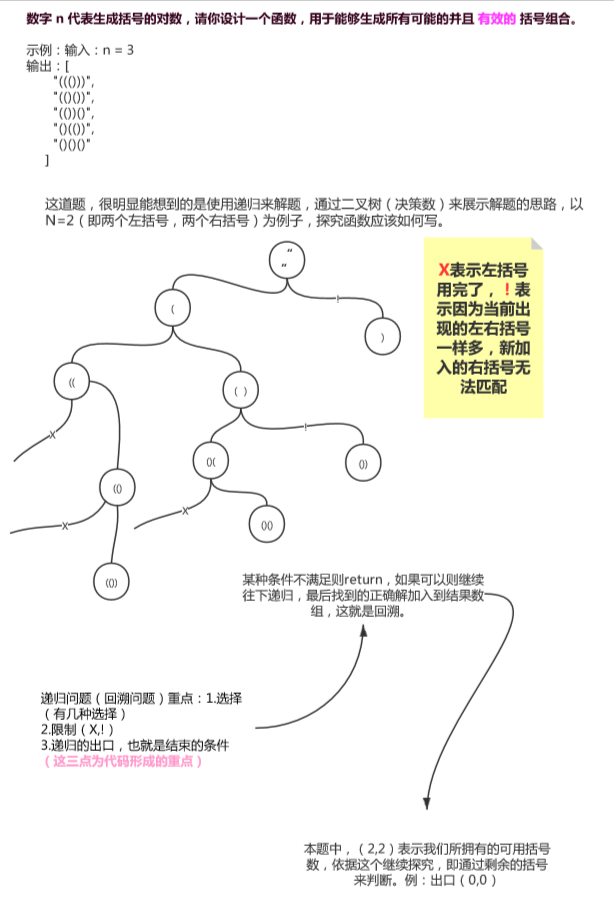
三、上面那道题的练习代码

function shenduchazhao(n) {
  const res = [];
  function dfs(leftRemain, rightRemain, str) {
    // 递归出口（左右括号都用完了）
    if (leftRemain === 0 && rightRemain === 0) {
      res.push(str);
     return;
    }
    // 先序遍历（前序遍历）
    // 如果都不满足这俩条件 结束dfs 就会回溯 继续考察
    // 左括号就能用 没有限制因为她始终可以期待一个右括号与之匹配
    if (leftRemain > 0) {
      dfs(leftRemain - 1, rightRemain, `${str}(`);
    }
    // 当左括号小于右括号的时候可以使用右括号
    if (leftRemain < rightRemain) {
      dfs(leftRemain, rightRemain - 1, `${str})`);
    }
  }
  dfs(n, n, '');
  return res;
}

 

shenduchazhao(3)

显示如下：