Mysql索引机制(B+Tree)
1，索引谁实现的：
索引是搜索引擎去实现的，在建立表的时候都会指定，搜索引擎是一种插拔式的，根据自己的选择去决定使用哪一个。
2，索引的定义：
索引是为了加速对表中数据行的检索而创建的一种分散存储的（不连续的）数据结构，硬盘级的。
索引意义：索引能极大的减少存储引擎需要扫描的数据量，索引可以把随机IO变成顺序IO。索引可以帮助我们在进行分组、排序等操作时，避免使用临时表。正确的创建合适的索引是提升数据库查询性能的基础。
3，为什么选择B+Tree：
B+树索引是B+树在数据库中的一种实现，是最常见也是数据库中使用最为频繁的一种索引。B+树中的B代表平衡（balance），而不是二叉（binary），因为B+树是从最早的平衡二叉树演化而来的。先了解二叉查找树、平衡二叉树（AVLTree）和平衡多路查找树（B-Tree），B+树即由这些树逐步优化而来。
二叉查找树：
二叉树具有以下性质：左子树的键值小于根的键值，右子树的键值大于根的键值。 如下图所示就是一棵二叉查找树，:
对该二叉树的节点进行查找发现深度为1的节点的查找次数为1，深度为2的查找次数为2，深度为n的节点的查找次数为n，因此其平均查找次数为 (1+2+2+3+3+3) / 6 = 2.3次。二叉查找树可以任意地构造，同样是2,3,5,6,7,8这六个数字，也可以按照下图的方式来构造：
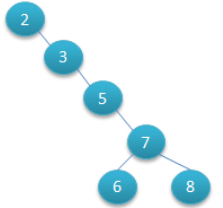
但是这棵二叉树的查询效率就低了。因此若想二叉树的查询效率尽可能高，需要这棵二叉树是平衡的，从而引出新的定义——平衡二叉树，或称AVL树。
平衡二叉树（AVL Tree）：
平衡二叉树（AVL树）在符合二叉查找树的条件下，还满足任何节点的两个子树的高度最大差为1。下面的两张图片，左边是AVL树，它的任何节点的两个子树的高度差<=1；右边的不是AVL树，其根节点的左子树高度为3，而右子树高度为1；
如果在AVL树中进行插入或删除节点，可能导致AVL树失去平衡，这种失去平衡的二叉树可以概括为四种姿态：LL（左左）、RR（右右）、LR（左右）、RL（右左）。它们的示意图如下：
这四种失去平衡的姿态都有各自的定义：
LL：LeftLeft，也称“左左”。插入或删除一个节点后，根节点的左孩子（Left Child）的左孩子（Left Child）还有非空节点，导致根节点的左子树高度比右子树高度高2，AVL树失去平衡。
RR：RightRight，也称“右右”。插入或删除一个节点后，根节点的右孩子（Right Child）的右孩子（Right Child）还有非空节点，导致根节点的右子树高度比左子树高度高2，AVL树失去平衡。
LR：LeftRight，也称“左右”。插入或删除一个节点后，根节点的左孩子（Left Child）的右孩子（Right Child）还有非空节点，导致根节点的左子树高度比右子树高度高2，AVL树失去平衡。
RL：RightLeft，也称“右左”。插入或删除一个节点后，根节点的右孩子（Right Child）的左孩子（Left Child）还有非空节点，导致根节点的右子树高度比左子树高度高2，AVL树失去平衡。
AVL树失去平衡之后，可以通过旋转使其恢复平衡。下面分别介绍四种失去平衡的情况下对应的旋转方法。
LL的旋转。LL失去平衡的情况下，可以通过一次旋转让AVL树恢复平衡。步骤如下：
- 将根节点的左孩子作为新根节点。
- 将新根节点的右孩子作为原根节点的左孩子。
- 将原根节点作为新根节点的右孩子。
LL旋转示意图如下：
RR的旋转：RR失去平衡的情况下，旋转方法与LL旋转对称，步骤如下：
- 将根节点的右孩子作为新根节点。
- 将新根节点的左孩子作为原根节点的右孩子。
- 将原根节点作为新根节点的左孩子。
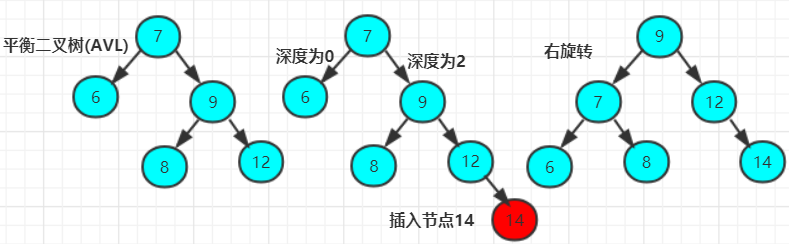
LR的旋转：LR失去平衡的情况下，需要进行两次旋转，步骤如下：
- 围绕根节点的左孩子进行RR旋转。
- 围绕根节点进行LL旋转。
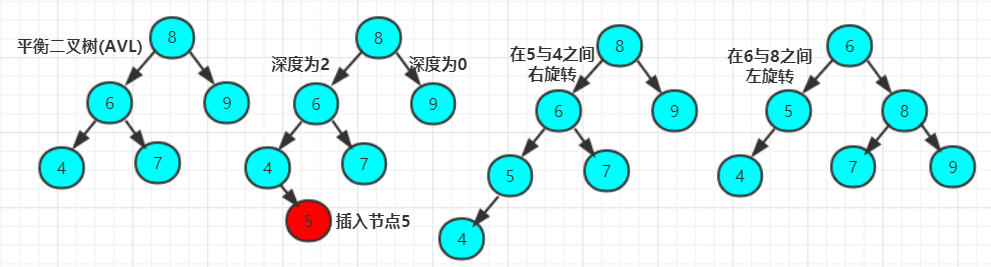
RL的旋转：RL失去平衡的情况下也需要进行两次旋转，旋转方法与LR旋转对称，步骤如下：
- 围绕根节点的右孩子进行LL旋转。
- 围绕根节点进行RR旋转。
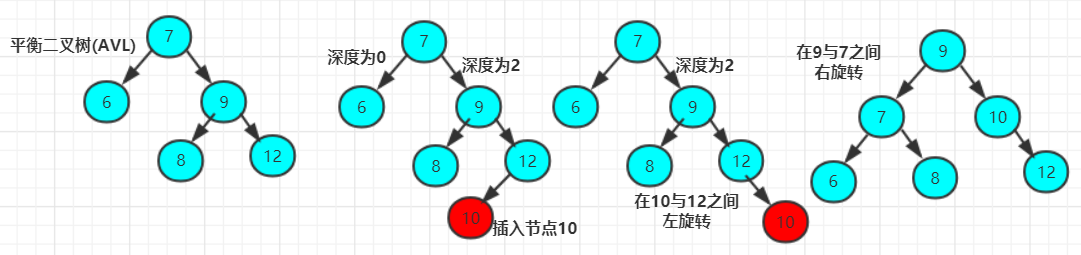
那么使用平衡二叉树作为索引数据结构的话会是怎么样的呢？先看一下下图：
可以把每个节点看成一个磁盘块，每个磁盘块存储的信息如右边这个结构图所示。
关键字：即我们建立索引的关键字段的对应值。
数据区：即关键字对应的数据存储磁盘位置，通过关键字所对应的磁盘位置进行IO读写操作获取数据。
节点引用：即指向子节点的磁盘位置。
如果要查找ID为8的数据，那么先会获取根节点10加载到内存中，比较数据大小，发现比10小，那么查找左节点5，发现比5大，查找5的右节点，发现命中，然后根据数据区地址去进行IO读写操作。但是B-Tree有如下缺点：
它太深了，数据处的（高）深度决定着他的IO操作次数，IO操作耗时大。它太小了，每一个磁盘块（节点/页）保存的数据量太小了。没有很好的利用操作磁盘IO的数据交换特性，一次IO操作以页为单位 ，4KB，那么加载一次绝对不会达到4KB.也没有利用好磁盘IO的预读能力（空间局部性原理），从而带来频繁的IO操作
平衡多路查找树（B-Tree）：
B-Tree是为磁盘等外存储设备设计的一种平衡查找树。因此在讲B-Tree之前先了解下磁盘的相关知识。
系统从磁盘读取数据到内存时是以磁盘块（block）为基本单位的，位于同一个磁盘块中的数据会被一次性读取出来，而不是需要什么取什么。InnoDB存储引擎中有页（Page）的概念，页是其磁盘管理的最小单位。InnoDB存储引
擎中默认每个页的大小为16KB，可通过参数innodb_page_size将页的大小设置为4K、8K、16K，在MySQL中可通过如下命令查看页的大小：mysql> show variables like 'innodb_page_size';
而系统一个磁盘块的存储空间往往没有这么大，因此InnoDB每次申请磁盘空间时都会是若干地址连续磁盘块来达到页的大小16KB。InnoDB在把磁盘数据读入到磁盘时会以页为基本单位，在查询数据时如果一个页中的每条数据都
能有助于定位数据记录的位置，这将会减少磁盘I/O次数，提高查询效率。B-Tree结构的数据可以让系统高效的找到数据所在的磁盘块。为了描述B-Tree，首先定义一条记录为一个二元组[key, data] ，key为记录的键值，对应表中的主键
值，data为一行记录中除主键外的数据。对于不同的记录，key值互不相同。一棵m阶的B-Tree有如下特性：
1. 每个节点最多有m个孩子。
2. 除了根节点和叶子节点外，其它每个节点至少有Ceil(m/2)个孩子。
3. 若根节点不是叶子节点，则至少有2个孩子
4. 所有叶子节点都在同一层，且不包含其它关键字信息
5. 每个非终端节点包含n个关键字信息（P0,P1,…Pn, k1,…kn）
6. 关键字的个数n满足：ceil(m/2)-1 <= n <= m-1
7. ki(i=1,…n)为关键字，且关键字升序排序。
8. Pi(i=1,…n)为指向子树根节点的指针。P(i-1)指向的子树的所有节点关键字均小于ki，但都大于k(i-1)
B-Tree中的每个节点根据实际情况可以包含大量的关键字信息和分支，如下图所示为一个3阶的B-Tree: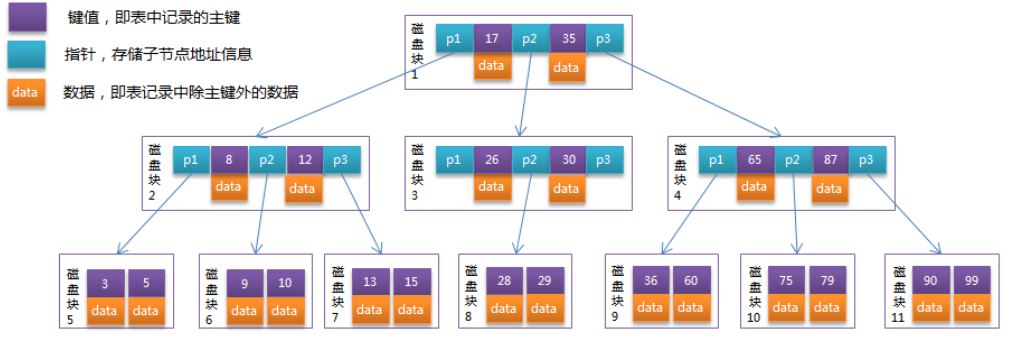
每个节点占用一个盘块的磁盘空间，一个节点上有两个升序排序的关键字和三个指向子树根节点的指针，指针存储的是子节点所在磁盘块的地址。两个关键词划分成的三个范围域对应三个指针指向的子树的数据的范围域。以根节点为例，关键字为17和35，P1指针指向的子树的数据范围为小于17，P2指针指向的子树的数据范围为17~35，P3指针指向的子树的数据范围为大于35。模拟查找关键字29的过程：
- 根据根节点找到磁盘块1，读入内存。【磁盘I/O操作第1次】
- 比较关键字29在区间（17,35），找到磁盘块1的指针P2。
- 根据P2指针找到磁盘块3，读入内存。【磁盘I/O操作第2次】
- 比较关键字29在区间（26,30），找到磁盘块3的指针P2。
- 根据P2指针找到磁盘块8，读入内存。【磁盘I/O操作第3次】
- 在磁盘块8中的关键字列表中找到关键字29。
分析上面过程，发现需要3次磁盘I/O操作，和3次内存查找操作。由于内存中的关键字是一个有序表结构，可以利用二分法查找提高效率。而3次磁盘I/O操作是影响整个B-Tree查找效率的决定因素。B-Tree相对于AVLTree缩减了节点个数，使每次磁盘I/O取到内存的数据都发挥了作用，从而提高了查询效率。
我们可以来算一笔账，以InnoDB存储引擎中默认每个页的大小为16KB来计算，假设以int型的ID作为索引关键字，那么 一个int占用4byte，由上图可以知道还有其他的除主键以外的数据，姑且页当成4byte，那么这里就是8byte，那么16KB=16*1024byte，那么我们在这种场景下，可以定义这个B-Tree的阶树为 （16*1024）/8=2048.那么这个树将会有2048-1路，也就是原来平衡二叉树(两路)的1024倍左右，从而大大提高了查找效率与降低IO读写次数。
B-Tree为了保证绝对平衡他有自己的机制，比如每个节点上的关键字个数=路数（阶数-1），如下图：
可以看到添加节点后违反了原有的规则，这个时候会进行分裂。结果就会形成一根最新的树，（如果分裂过程中23 333 这个节点页不满足了会继续向上分裂）：
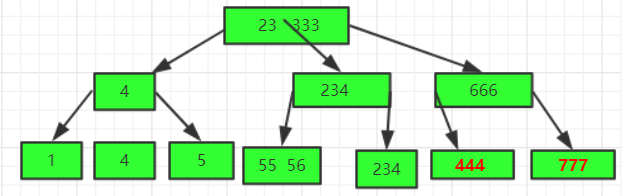
所以建立合适的索引是很重要的 ，不宜多，当加一条数据，整棵树会进行重组。
B+Tree：
B+Tree是在B-Tree基础上的一种优化，使其更适合实现外存储索引结构，InnoDB存储引擎就是用B+Tree实现其索引结构。
从 B-Tree 结构图中可以看到每个节点中不仅包含数据的key值，还有data值。而每一个页的存储空间是有限的，如果data数据较大时将会导致每个节点（即一个页）能存储的key的数量很小，当存储的数据量很大时同样会导致B-Tree的深度较大，增大查询时的磁盘I/O次数，进而影响查询效率。在B+Tree中，所有数据记录节点都是按照键值大小顺序存放在同一层的叶子节点上，而非叶子节点上只存储key值信息，这样可以大大加大每个节点存储的key值数量，降低B+Tree的高度。
B+Tree相对于B-Tree有几点不同：
- B+节点关键字搜索采用闭合区间
- B+非叶节点不保存数据相关信息，只保存关键字和子节点的引用
- B+关键字对应的数据保存在叶子节点中
- B+叶子节点是顺序排列的，并且相邻节点具有顺序引用的关系
将B-Tree优化，由于B+Tree的非叶子节点只存储键值信息，假设每个磁盘块能存储4个键值及指针信息，则变成B+Tree后其结构如下图所示：
通常在B+Tree上有两个头指针，一个指向根节点，另一个指向关键字最小的叶子节点，而且所有叶子节点（即数据节点）之间是一种链式环结构。因此可以对B+Tree进行两种查找运算：一种是对于主键的范围查找和分页查找，另一种是从根节点开始，进行随机查找。可能上面例子中只有22条数据记录，看不出B+Tree的优点，下面做一个推算：InnoDB存储引擎中页的大小为16KB，一般表的主键类型为INT（占用4个字节）或BIGINT（占用8个字节），指针类型也一般为4或8个字节，也就是说一个页（B+Tree中的一个节点）中大概存储16KB/(8B+8B)=1K个键值（因为是估值，为方便计算，这里的K取值为〖10〗^3）。也就是说一个深度为3的B+Tree索引可以维护10^3 * 10^3 * 10^3 = 10亿 条记录。
实际情况中每个节点可能不能填充满，因此在数据库中，B+Tree的高度一般都在2~4层。mysql 的InnoDB存储引擎在设计时是将根节点常驻内存的，也就是说查找某一键值的行记录时最多只需要1~3次磁盘I/O操作。数据库中的B+Tree索引可以分为聚集索引（clustered index）和辅助索引（secondary index）。上面的B+Tree示例图在数据库中的实现即为聚集索引，聚集索引的B+Tree中的叶子节点存放的是整张表的行记录数据。辅助索引与聚集索引的区别在于辅助索引的叶子节点并不包含行记录的全部数据，而是存储相应行数据的聚集索引键，即主键。当通过辅助索引来查询数据时，InnoDB存储引擎会遍历辅助索引找到主键，然后再通过主键在聚集索引中找到完整的行记录数据。
B+Tree在MYSQL中采用的是左闭合区间，MYSQL推崇使用ID作为索引，由于ID是自增的数字类型，只会增大，所以采用向右拓展的一个方式，从根节点进行比对，由于枝节点不保存数据，无所谓命不命中，都要继续走到叶子节点才能加载数据。
B+树是B-树的变种（PLUS版）多路绝对平衡查找树，他拥有B-树的优势。
B+树扫库、表能力更强。
B+树的磁盘读写能力更强。
B+树的排序能力更强。
B+树的查询效率更加稳定（仁者见仁、智者见智）。
4，B+Tree在两大引擎中如何体现：
索引的实现是由搜索引擎来实现的，那么在 MYSQL中比较主流的两大引擎是：Myisam 跟 innoDB，存储引擎是建立在表上面的，在建立表的时候可以指定所需要的搜索引擎。例如下列的创建语句中就指定了搜索引擎为：ENGINE=InnoDB，不指定就使用默认的InnoDB
CREATE TABLE `user` ( `id` int(11) NOT NULL, `name` varchar(255) DEFAULT NULL, PRIMARY KEY (`id`) ) ENGINE=InnoDB DEFAULT CHARSET=utf8;
B+Tree 在 Myisam 中的体现：
在创建好表结构并且指定搜索引擎为 Myisam之后，会在数据目录生成3个文件，分别是table_name.frm(表结构文件)，table_name.MYD（数据保存文件）,table_name.MYI（索引保存文件）。
例如上诉 teacher表，两个文件分别保存了数据及索引，由于B+Tree中只有叶子节点保存数据区，在Myisam中，数据区中保存的是数据的引用地址，就比如说ID为101的数据信息所保存到物理磁盘地址为 0x123456,在索引中的节点数据去中所保存的就是这个磁盘地址指针。当扫描到这个指针位置，就可以通过这个磁盘指针讲数据加载出来。
在Myisam中B+Tree的实现中比如现在不用ID作为索引了，要用name，那么他的一个展现形式有事怎么样的呢？其实他与ID作为索引是一样的，也是保存他指定的磁盘位置指针，他们是平级的。如下图：
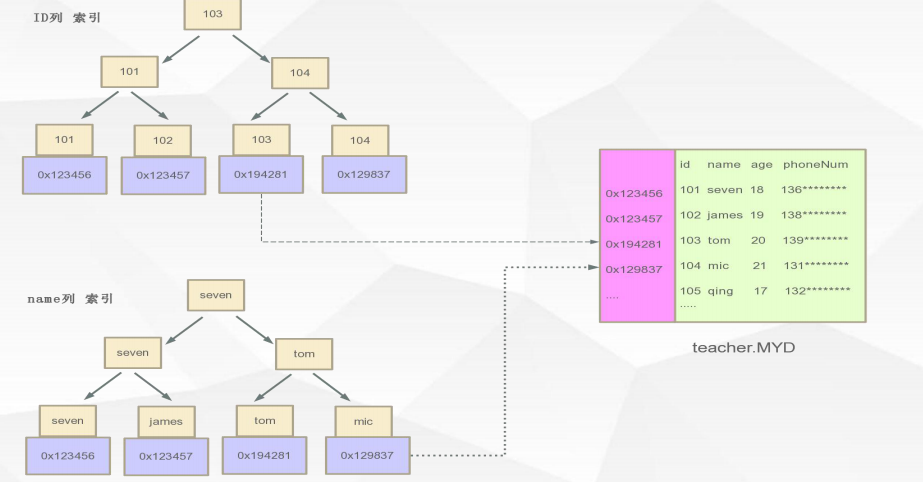
B+Tree 在 InnoDB 中的体现：
在创建好表结构并且指定搜索引擎为 InnoDB之后，会在数据目录生成3个文件，分别是table_name.frm(表结构文件)，table_name.idb（数据与索引保存文件）。
在 InnoDB中，因为设计之初就是认为主键是非常重要的。是以主键为索引来组织数据的存储，当我们没有显示的建立主键索引的时候，搜索引擎会隐式的为我们建立一个主键索引以组织数据存储。数据库表行中数据的物理顺序与键值的逻辑（索引）顺序相同，InnoDB就是以聚集索引来组织数据的存储的，在叶子节点上，保存了数据的所有信息。如果这个时候建立了name字段的索引：
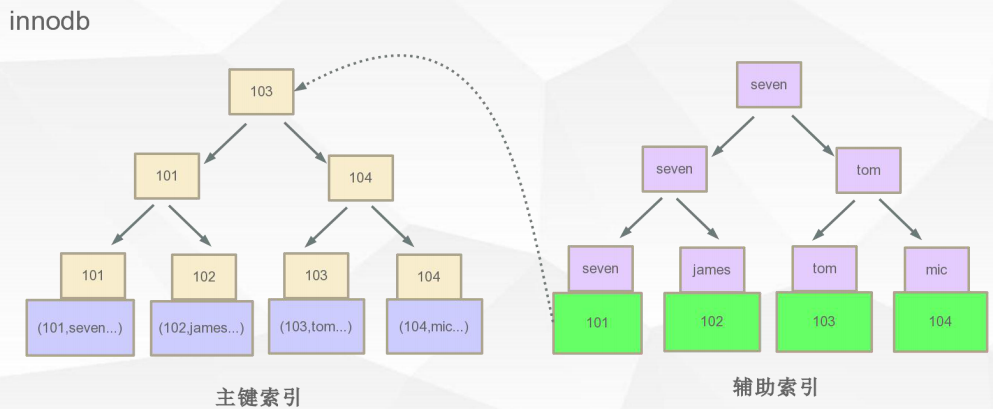
会产生一个辅助索引，即name字段的索引，而此刻叶子节点上所保存的数据为 聚集索引（ID索引）的关键字的值，基于辅助索引找到ID索引的值，再通过ID索引区获取最终的数据。这个做法的好处是在于产生数据迁移的时候只要ID没发生变法，那么辅助索引不需要重新生成，不这么做的话，如果存储的是磁盘地址的话，在数据迁移后所有辅助索引都需要重新生成。
5，索引知识：
找出离散性最好的列：
越大离散型越好 count(distinct col):count(col) 理解为差异性。结论：离散性越高选择性就越好，比如有一个性别的字段的索引，假设男为1，女为0：就会生成一下一个索引树：
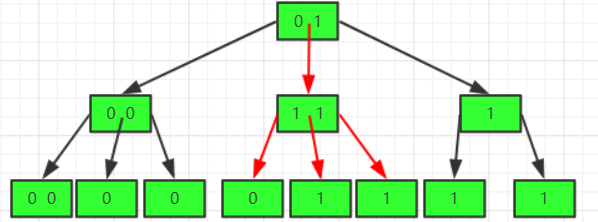
这个时候要搜索女的数据，那么在根节点触发，可以由两条路可以走，从中间走下去的话发现可以选择的线路太多了，这样会导致搜索引擎懵逼，优化器觉得既然要搜索这么多数据，还不如全表扫描呢，这就导致离散型降低。不利于性能。
最左匹配原则：
对索引中关键字进行计算（对比），一定是从左往右依次进行，且不可跳过，在创建数据库的时候需要选择字符集及排序规则，这都是有用的 ，比如一棵B-tree中的根节点为一个字符串 abc ，那么我现在要搜索一个为 adc的索引关键字的数据，根节点abc的ASCII 码为 97 98 99，而 adc的为 97 100 99，那么和3个数字会逐一比对，且100>98，接下去一定会走右子树。
联合索引：
单列索引：节点中关键字[name] 及索引的关键字的值为那么对应的值 ，比如 张三。
联合索引：节点中关键字[name,phoneNum]比如张三，138888888。
联合索引列选择原则。
- 经常用的列优先 【最左匹配原则】。
- 选择性（离散度）高的列优先【离散度高原则】。
- 宽度小的列优先【最少空间原则】。
示例：经排查发现最常用的sql语句：Select * from users where name = ? ;Select * from users where name = ? and phoneNum = ?;
机灵的李二狗的解决方案：create index idx_name on users(name);--（冗余索引 最左原则，下面这个联合索引适用于以上2个sql语句）；create index idx_name_phoneNum on users(name,phoneNum);
所以在这种情况下只需要建立一个联合索引即可，会根据最左匹配原则去匹配的。
覆盖索引：
如果查询列可通过索引节点中的关键字直接返回，则该索引称之为覆盖索引。覆盖索引可减少数据库IO，将随机IO变为顺序IO，可提高查询性能。比说所建立了一个联合索引 reate index idx_name_phoneNum on users(name,phoneNum);而此刻有sql select name phoneNum from 。。。。这个就是覆盖索引。
6，总结及验证：
索引列的数据长度能少则少。索引一定不是越多越好，越全越好，一定是建合适的。查询条件上有计算函数无法命中索引。
匹配列前缀：like 9999%（最原则上按照左匹配上来说是可以的，但是不一定能用到索引，当离散性太差的时候就不行），like %9999%（不行）、like %9999（不行）用不到索引；
Where 条件中 not in 和 <>操作无法使用索引；匹配范围值，order by 也可用到索引；多用指定列查询，只返回自己想到的数据列，少用select *；
联合索引中如果不是按照索引最左列开始查找，无法使用索引；
联合索引中精确匹配最左前列并范围匹配另外一列可以用到索引；比如联合索引【name，phoneNum】，当SQL为：select .....where name='1' and phoneNum>xxxxxxx.
联合索引中如果查询中有某个列的范围（大于小于）查询，则其右边的所有列都无法使用索引；
最后送上一首网友提供的打油诗：
全值匹配我最爱，最左前缀要遵守；
带头大哥不能死，中间兄弟不能断；
索引列上少计算，范围之后全失效；
Like百分写最右，覆盖索引不写星；
不等空值还有or，索引失效要少用；
VAR引号不可丢，SQL高级也不难！
