素数的判断

定义：

　　素数指在大于1的自然数中，除了1和此整数自身外，无法被其他自然数整除的数（也可以定义为只有1和本身两个因数的数）。比1大的不是素数的数称为合数。1和0既非素数也非合数。素数在数论中有着很重要的地位。

判断：

　　1，检查一个整数n是否为素数就，是要判定整数n能否被除1和它自身之外的任意整数整除，若都不能整除，则n为素数。【效率低】

　　2，检查一个正整数是否为素数，最简单的方法就是试除法，将该数用小于等于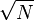的所有素数去试除，若均无法整除，则为素数。因为如果一个数不是素数是合数（除了1和0）， 那么一定可以由两个自然数相乘得到， 其中一个大于或等于它的平方根，一个小于或等于它的平方根。并且成对出现。 【效率高】

 

#include <iostream>
#include <cmath>

using namespace std;

//函数在调用之前必须先声明
bool prime(int n);

int main()
{
    int i;
    
    //设置一个死循环，当用户输入0的时候终止循环
    
    while (true)
    {
          cout << "请输入一个数字，并按Enter。";
          cin >> i;
          if (i == 0)
          {
                break;
          } 
          if (prime(i))
          {
                       cout << i << " 是质数." << endl; 
          }
          else 
          {
               cout << i << " 不是质数。" << endl;
          }
    } 
    
    system ("PAUSE");
    return 0; 
} 

bool prime(int n)
{
      int i;
      
      for (i = 2; i <= sqrt(n); i++)
      {
          if (n % i == 0)
          {
                return false;
          }
      }
      return true; 
}

有个问题还没有解决，就是这个程序在DEV-CPP的编译环境中通不过，提示sqrt()函数需要double类型的数据，可以改了之后还是没通过，求解？