Python 基础算法
递归
时间&空间复杂度
常见列表查找
算法排序
数据结构
递归
在调用一个函数的过程中,直接或间接地调用了函数本身这就叫做递归。
注:python在递归中没用像别的语言对递归进行优化,所以每一次调用都会基于上一次的调用进行,并且他设置了最大递归数量防止递归溢出
递推:每一次都是基于上一次进行下一次执行
回溯:在遇到终止条件,则从最后往回一级级把值返回来
递归的特点:
1、调用自身
2、结束条件 ===> (有穷)
时间&空间复杂度
时间复杂度
算法的时间复杂度是一个函数,它定量描述了该算法的运行时间,时间复杂度常用o表述,适用这种方式时,时间复杂度可被称为是渐进的,它考察当输入值大小趋近无穷时的情况
时间复杂度是用来估计算法运行时间的一个式子。一般来说,时间复杂度高的算法比复杂度低的算法慢
常见的时间复杂度(按效率排序):o(1)<o(logn)<o(n)<o(nlogn)<o(n^2)
不常见的时间复杂度:o(n!) o(2^n) o(n^n)
print('Hello world') # O(1) # O(1) print('Hello World') print('Hello Python') print('Hello Algorithm') for i in range(n): # O(n) print('Hello world') for i in range(n): # O(n^2) for j in range(n): print('Hello world') for i in range(n): # O(n^2) print('Hello World') for j in range(n): print('Hello World') for i in range(n): # O(n^2) for j in range(i): print('Hello World') for i in range(n): for j in range(n): for k in range(n): print('Hello World') # O(n^3)
如何判断时间复杂度?
1、循环减半的过程 ==> o(logn)
2、几次循环就是n的几次方的复杂度
空间复杂度
空间复杂度:用来评估算法内存占用大小的一个式子
a = 'Python' # 空间复杂度为1 # 空间复杂度为1 a = 'Python' b = 'PHP' c = 'Java' num = [1, 2, 3, 4, 5] # 空间复杂度为5 num = [[1, 2, 3, 4], [1, 2, 3, 4], [1, 2, 3, 4], [1, 2, 3, 4], [1, 2, 3, 4]] # 空间复杂度为5*4 num = [[[1, 2], [1, 2]], [[1, 2], [1, 2]] , [[1, 2], [1, 2]]] # 空间复杂度为3*2*2
定义一个或多个变量,空间复杂度都是为1,列表的空间复杂度为列表的长度
常见列表查找
首先我们先定义一个装饰器,为了后期比较各个算法(无论是排序,还是查找)的时间。
import time def cal_time(func): def wrapper(*args, **kwargs): t1 = time.time() result = func(*args, **kwargs) t2 = time.time() print('%s running time : %s seconds.' % (func.__name__, t2-t1)) return wrapper
1、顺序查找
遍历所有元素,查找出对应的。也叫做线性查找
def line_search(data_set, val): for i in range(len(data_set)): if data_set[i] == val: return i
2、二分查找
在计算机科学中,二分搜索(binary search),是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半
# 二分查找法 建立在有序区间的基础上实现 def bin_search(data_set, val): low = 0 high = len(data_set) - 1 # 定义最小最大下标 while low <= high: # 循环 mid = (low + high) // 2 # 取中间值的整数 if data_set[mid] == val: # 如果中间值等于查询值,返回 return mid elif data_set[mid] < val: # 如果中间值小于查询值,最小下标变成low + 1, 区间减半 low = mid + 1 else: high = mid - 1 # 同理最大下标变成mid-1, 区间减半
两种查找方法的时间复杂度分别为
线性查找:o(n) 二分查找:o(logn)
测试一下:
@cal_time def _bin_search(data_set, val): bin_search(data_set, val) # 不能把装饰器直接用来装饰递归函数,不然会伴随递归函数一起递归的 import random import copy data = [i for i in range(10000000)] line_search(data, 99990009) _bin_search(data, 99990009)
时间效率:
/Library/Frameworks/Python.framework/Versions/3.6/bin/python3 /Users/dandyzhang/PycharmProjects/untitled/综合/算法/算法查找.py line_search running time : 0.6025080680847168 seconds. _bin_search running time : 1.52587890625e-05 seconds. Process finished with exit code 0
算法排序
常用的排序算法:冒泡排序,插入排序,归并排序, 快速排序、基数排序、堆排序,选择排序。
首先,我们先来剖析一下最常见的lowB三人组:冒泡排序,选择排序,插入排序。
1. 冒泡排序
冒泡排序(Bubble Sort)是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元n个项目需要O(n^2) 的比较次数,且可以原地排序。尽管这个算法是最简单了解和实现的排序算法之一,但它对于包含大量的元素的数列排序是很没有效率的
最优时间复杂度: O(n)
最坏时间复杂度: O(n^2)
稳定性:稳定的排序
思路
列表相邻的数比较,换位置,最后一个在第一次循环肯定变成有序区的第一个元素,即最大的
# 冒泡排序 # 最好情况o(n) 一般情况o(n^2) 最坏情况o(n^2) @cal_time def bubble_sort(li): for i in range(len(li) -1): for j in range(len(li) - i - 1): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1], li[j] # 冒泡排序优化 @cal_time def bubble_sort_1(li): for i in range(len(li) -1): exchange = False for j in range(len(li) - i - 1): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1], li[j] exchange = True if not exchange: # 可能一次没减少,可能是排好序的省了全部的循环,只走了一趟 break
测试一下冒泡排序及其优化版的时间:
data = list(range(5000)) random.shuffle(data) # 打乱列表顺序,如果注释掉这一句,就是极端情况 bubble_sort(data) bubble_sort_1(data) # 绝大多数情况下都会是比第一种快的 # 冒泡排序分为最好情况,一般情况, 最坏情况, 时间复杂度是不一样的 bubble_sort running time : 2.3754842281341553 seconds. bubble_sort_1 running time : 0.0004961490631103516 seconds.
2.选择排序
最优时间复杂度:O(n^2)
最坏时间复杂度:O(n^2)
稳定性:不稳定的排序
思路
一趟便利记录最小的数,放到第一个位置;再遍历记录剩余列表中最小数,继续放置;
# 选择排序法 @cal_time def select_sort(li): for i in range(len(li) - 1): min_loc = i # 设置初始值永远为第一位数, 循环跟后面的数进行比较 for j in range(i + 1, len(li)): # 不需要跟自身相比,所以+1 if li[j] < li[min_loc]: # 如果后面循环到的数小于现在认为的最小位置 min_loc = j # 记录下循环到的数的下标 li[i], li[min_loc] = li[min_loc], li[i] # 循环结束后取最小的下标跟当前比对的位置互换 select_sort(data)
3.插入排序
最坏时间复杂度: O(n^2)
最优时间复杂度: O(n)
稳定性:稳定的排序
思路
跟打扑克牌抓牌的操作很相似,抓牌的时候跟有序区进行遍历的比较,插入在合适的位置
@cal_time def insert_sort(li): for i in range(1, len(li)): # 从1开始 tmp = li[i] # 循环到的需要跟有序区进行对比的数 j = i - 1 # 循环到的数跟之前的有序区进行比较 while j >= 0 and li[j] > tmp: # 比较的位置不在最左边并且循环到的需要对比的数小于有序区的被比较的数 li[j+1] = li[j] # 有序区被比较的数向右移动一位 j = j -1 # 递减往左比较 li[j + 1] = tmp # li[j+1] = li[j] ==> 比如3的位置的值被放到4号了,3号空了应该放在3号,但是下面又减了1,所以是j+1 # -1的话,直接+1到起始位置0,另外提一个没什么卵用的优化,遍历有序区查找,其实可以用二分查找插入点,但是位置还是要一个个移动,所以。。。 insert_sort(data)
这次测试下lowB三人组的时间
data = [i for i in range(5000)] random.shuffle(data) data1 = copy.deepcopy(data) data2 = copy.deepcopy(data) data3 = copy.deepcopy(data) bubble_sort(data) bubble_sort_1(data1) select_sort(data2) insert_sort(data3)
bubble_sort running time : 2.424175977706909 seconds.
bubble_sort_1 running time : 2.353872776031494 seconds.
select_sort running time : 0.9465441703796387 seconds.
insert_sort running time : 1.176313877105713 seconds.
***************************************************************************************************************************************
下面研究下比较高端的排序
快速排序
思路
1、取一个元素p(第一个元素),使元素p归位
2、列表被p分成两部分,左边都比p小,右边都比p大
3、递归完成排序
# 快速排序 时间复杂度nlogn def quick_sort_x(data, left, right): # 建立模型,已经存在左右两块区域 if left < right: mid = partition(data, left, right) # 分区 quick_sort_x(data, left, mid - 1) # 递归左分区 quick_sort_x(data, mid + 1, right) # 递归右分区 def partition(data, left, right): # 分区,建立一个左边小,右边大的分区 tmp = data[left] # 取最左边的存入tmp,以此为指针 while left < right: # 左指针跟右指针没右碰到 while left < right and data[right] >= tmp: # 右边指向的数大于tmp right -= 1 # 继续循环 data[left] = data[right] # 右边的数小于tmp的时候移动到左边的left while left < right and data[left] <= tmp: # 左边的小于tmp left += 1 # 继续循环 data[right] = data[left] # 左边的大于tmp,指向的左边值放到右边 data[left] = tmp # 此时left跟right已经相等 也可以将tmp放在right return left # 同理也可以return right @cal_time def quick_sort(data): # 这个就不解释了,看灵性 return quick_sort_x(data, 0, len(data) - 1)
跟lowB三人组比较下:
data = list(range(5000)) random.shuffle(data) data1 = copy.deepcopy(data) data2 = copy.deepcopy(data) data3 = copy.deepcopy(data) data4 = copy.deepcopy(data) bubble_sort_1(data1) insert_sort(data2) select_sort(data3) quick_sort(data4) bubble_sort_1 running time : 2.3831076622009277 seconds. insert_sort running time : 1.2162189483642578 seconds. select_sort running time : 1.002126932144165 seconds. quick_sort running time : 0.012326955795288086 seconds. # 为什么叫快排,显而易见了。
绝大多数的语言 C++ /java都是快速排序,但python不是,python的排序跟快速排序是一个时间复杂度级别,C封装的。所以C的排序肯定是比python的排序还要快。
快排也不是一直都很快,比如一组数据都是按照倒序排好的,每次取最左边分区的话只能分得一个元素,时间复杂度可想而知。
快速排序的最坏情况
最好情况 o(nlogn)
一般情况o(nlogn)
最坏情况o(n^2)
先来比较下python系统内置排序跟快排。
系统内置排序
# 系统内置排序 @cal_time def sys_sort(data): return data.sort()
比较:
data = list(range(5000)) random.shuffle(data) data4 = copy.deepcopy(data) data5 = copy.deepcopy(data) quick_sort(data4) sys_sort(data5) quick_sort running time : 0.012069225311279297 seconds. sys_sort running time : 0.0011510848999023438 seconds.
可以发现python内置排序算法,比快速排序还要快的多得多。内置排序算法是什么呢?我也不知道,后续有空可以研究。
备注
上面的代码递归测试可能会遇到递归最大限度的问题。
解决方案
import sys sys.setrecursionlimit(10000)
快排遇到最坏情况可以反过来大小调换处理,大于换小于
def partition(data, left, right): tmp = data[left] while left < right: while left < right and data[right] <= tmp: # mark1 right -= 1 data[left] = data[right] while left < right and data[left] >= tmp: # mark2 left += 1 data[right] = data[left] data[left] = tmp return left
堆排序
在引入堆排序的思想之前,先补充下二叉树的知识。
https://baike.baidu.com/item/%E4%BA%8C%E5%8F%89%E6%A0%91/1602879?fr=aladdin
只是找个链接让大家了解二叉树概念:
树 二叉树 ==》 特殊的树,父节点只有2个子节点 完全二叉树 ==》 从后往前不能隔断的二叉树 满二叉树 ==》 全部节点都有的二叉树 大根堆&小根堆 ==》 根结点是最大或最小的
思路:
子节点中最大的跟父节点比较,上位,从下往上攀登
# 堆排序 def shift(data, low, high): i = low j = 2 * i + 1 tmp = data[i] while j <= high: # 孩子在堆里 if j < high and data[j] < data[j + 1]: # j < high代表有右孩子, 并且右孩子比左孩子大 j += 1 if tmp < data[j]: # 如果父节点小于最大的孩子节点 data[i] = data[j] # 最大的孩子节点上位 i = j # 孩子成为新父节点 j = 2 * i + 1 # 新孩子节点 else: break data[i] = tmp # 上位完的孩子节点,或者本身 @cal_time def heap_sort(data): # 升序 n = len(data) for i in range(n // 2 - 1, -1, -1): # n//2-1 最后一个有孩子的父亲的下标 shift(data, i, n-1) # 堆建好了 for i in range(n - 1, -1, -1): # i指向堆的最后 data[0], data[i] = data[i], data[0] # 父节点下位,孩子节点上去 shift(data, 0, i - 1) # 调整出新的父节点,大的树放在最左节点,不再参与循环 def heap_sort(data): # li 降序 n = len(data) for i in range(n // 2 - 1, -1, -1): # n//2-1 最后一个有孩子的父亲的下标 shift(data, i, n-1) # 堆建好了 li = [] for i in range(n - 1, -1, -1): # i指向堆的最后 li.append(data[0]) data[i] = data[0] shift(data, 0, i - 1) # 调整出新的父节点
归并排序
思路
两段有序列表,一次次相互比较拿最小的 ==> 操作被称为一次归并
1、分解:将列表越分越小,直至分成一个元素
2、一个元素是有序的
3、合并:将两个有序列表归并,列表越来越大
简述就是:先递归到最小单位下进行大小比较,调整位置,再往上进行合并比对调整

时间复杂度:o(nlogn) 空间复杂度:o(n)
代码实现:
def merge(li, low, mid, high): i = low j = mid + 1 ltmp = [] # 实际上i,j已经将区分好,0~mid | mid+1 high while i <= mid and j <= high: # 当两边指针都没有走完的时候 if li[i] < li[j]: # 如果左边小于右边的把左边的加入空列表,因为左右已经是有序的,所以一定是降序的了 ltmp.append(li[i]) i += 1 else: ltmp.append(li[j]) # 不满足的话,右边的一定小 j += 1 # 左指针或者右指针已经走完 while i <= mid: # 右指针走完,只剩左指针 ltmp.append(li[i]) i += 1 while j <= high: # 左指针走完,只剩右指针 ltmp.append(li[j]) j += 1 # print(ltmp) li[low: high + 1] = ltmp # 处理完,即拍完序,再赋值给原传入数组,右I/O操作!! def _mergesort(li, low, high): if low < high: # 左右指针不重合继续分区,最小化分区 mid = (low + high) // 2 # 中间指针 _mergesort(li, low, mid) # 左分区处理 _mergesort(li, mid + 1, high) #右分区处理 merge(li, low, mid, high) # 最小分区后合并排序 @cal_time # 不解释了 def mergesort(li, low, high): _mergesort(li, low, high)
上面三种快的排序算法进行比较:
data = list(range(100000, 0, -1)) random.shuffle(data) data1 = copy.deepcopy(data) data2 = copy.deepcopy(data) data3 = copy.deepcopy(data) quick_sort(data1) heap_sort(data2) mergesort(data3, 0, len(data) - 1) quick_sort running time : 0.3668999671936035 seconds. heap_sort running time : 0.5506401062011719 seconds. mergesort running time : 0.4741668701171875 seconds.
三种快的排序的缺点:
快速排序:极端情况下排序效率低
归并排序:需要额外的内存开销
堆排序:在快的排序算法中相对较慢
所以一般情况下:时间:快速排序 < 归并排序 < 堆排序
真的,再说最后一个。
希尔排序
观察一下”插入排序“:其实不难发现她有个缺点:
如果当数据是”5, 4, 3, 2, 1“的时候,此时我们将“无序块”中的记录插入到“有序块”时,估计俺们要崩盘,
每次插入都要移动位置,此时插入排序的效率可想而知。
shell根据这个弱点进行了算法改进,融入了一种叫做“缩小增量排序法”的思想,其实也蛮简单的,不过有点注意的就是:
增量不是乱取,而是有规律可循的。

思路:
是一种分组插入排序算法的优化
先取一个整数d = n//2,将元素从头开始,分为n//2个元素一组
取第二个整数 d1 = d // 2 同上
直到按1来分组
希尔排序每趟并不使某些元素有序,而是使整体数据越来越接近有序,最后一趟排序使得所有数据有序
时间复杂度:1.3n 或者 (1+T)n
@cal_time def mergesort(li, low, high): _mergesort(li, low, high) def shell_sort(li): gap = len(li) // 2 # 取差值 while gap >= 1: # 差值大于等于1 for i in range(gap, len(li)): # 第一组差值往后循环 tmp = li[i] # 后半区间的开始 j = i - gap # 间隔gap个的前一个数 while j >= 0 and tmp < li[j]: # 前一个数存在,tmp 小于前面的数 li[j + gap] = li[j] # 大的放后面 j -= gap # 减去一个差值,看是否存在前前个值 li[j + gap] = tmp gap /= 2
时间复杂度:
希尔排序的时间复杂度是所取增量序列的函数,尚难准确分析。有文献指出,当增量序列为d[k]=2^(t-k+1)时,希尔排序的时间复杂度为O(n^1.5), 其中t为排序趟数。
稳定性: 不稳定
希尔排序效果:
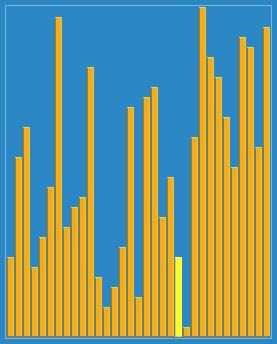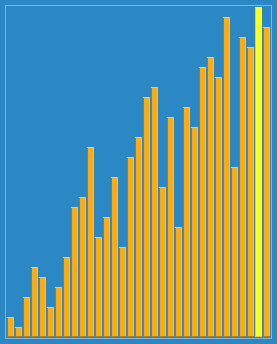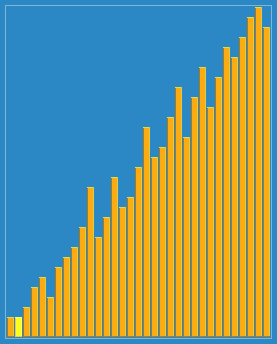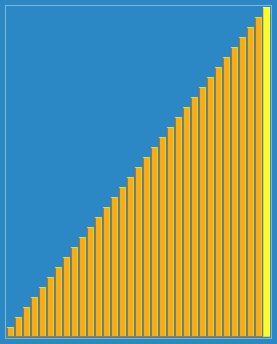
练习题
https://leetcode.com/problems/two-sum/?tab=Description
1、根据提供的整数,查找有序数列 返回下标范围
例如:a = [1,2,3,3,4,4,4,5,5,6,6]; val = 3; 返回(2,3)
data = [1,2,3,3,3,4,4,5] def bin_search(data, val): low = 0 high = len(data) - 1 while low <= high: mid = (low + high) // 2 if data[mid] == val: left = mid right = mid while left >= 0 and data[left] == val: left -= 1 while right <= high and data[right] == val: right += 1 return (left + 1, right -1) elif data[mid] < val: low = mid + 1 else: high = mid - 1 print(bin_search(data, 5))
2、列表[1,2,5,4]与目标整数3,返回2个加起来等于目标数的下标
例如1+2=3,结果为(0, 1)
data = [1, 2, 4, 5, 6] target = 3 # 方法一 循环试 for i in range(len(data)): for j in range(i, len(data)): if data[i] + data[j] == target: print(i, j) # 方法二 二分法 def bin_search(data, res, low, high): while low <= high: mid = (low + high) // 2 if data[mid] == res: return mid elif data[mid] < res: low = mid + 1 else: high = mid - 1 def func2(): import copy data2 = copy.deepcopy(data) for i in range(len(data2)): a = i b = bin_search(data2, target - data2[i], i + 1, len(data2) - 1) if b: return (data.index(data2[a]), data.index(data2.index(data2[b])))
3、约瑟夫问题
题目:有一组数首位比如0,1,2,3,4,5,6,7,8,以m为循环间隔数,杀掉从开始数第m个数,直到结束。
方法一:通过列表解决问题。
# 约瑟夫问题 # 1 2 3 4 5 6 7 8 9 # 0 1 2 3 4 5 6 7 8 # 循环去除隔4个的元素 def func(n, m): # n 总人数,m隔的数 people = [i for i in range(1, n + 1)] x = 0 while len(people) > 0: dead_location = (x + (m - 1)) % len(people) # 当前位置 + 下次循环的m 跟总长度取余 yield people.pop(dead_location) x = dead_location print(list(func(9, 4))) # 时间复杂度o(n^2)
方法二:通过链表解决问题
class LinkList: class Node: def __init__(self, item=None): self.item = item self.next = None class LinkListIterator: def __init__(self, node): self.node = node def __next__(self): if self.node: cur_node = self.node self.node = cur_node.next return cur_node.item else: raise StopIteration def __iter__(self): return self def __init__(self, iterable=None): self.head = LinkList.Node(0) self.tail = self.head self.extend(iterable) def append(self, obj): s = LinkList.Node(obj) self.tail.next = s self.tail = s def extend(self, iterable): for obj in iterable: self.append(obj) self.head.item += len(iterable) def remove_nth_node(self, node, m): for i in range(m - 2): node = node.next p = node.next node.next = p.next self.head.item -= 1 return p # p 可以删, 可以自动回收 def __iter__(self): return self.LinkListIterator(self.head.next) def __len__(self): return self.head.item def __str__(self): return '<<' + ','.join(map(str, self)) + '>>' def yuesefu_link(n, m): people = LinkList([i for i in range(1, n + 1)]) people.tail.next = people.head.next x = people.head.next while len(people) > 0: p = people.remove_nth_node(x, m) x = p.next yield p.item print(list(yuesefu_link(9,4))) # 时间复杂度 o(nm)





