砝码称重问题,因式分解有妙用
如果天平两端都允许放砝码,并且假定所有的砝码都是整数克。为了称出从 1 克到 40 克 所有整数克 的物品,最少需要几个砝码?
感兴趣的读者不妨自己先试着想想,再往下看。
秘密在于 3 的幂
说起来这个问题历史还算是挺悠久的。据《数学游戏与欣赏》( [英] 劳斯·鲍尔 [加] 考克斯特 著,杨应辰等 译),这个问题被称作巴协 (Bachet) 砝码问题;而据《数学聊斋》(王树禾著),该问题至少可追溯到 17 世纪法国梅齐里亚克 (Meziriac, 1624) 。他们给出的答案是:
最少需要 4 个砝码,规格分别为 1 克、3 克、9 克和 27 克。
例如,为了称出 2 克的物品,我们只需在天平一端放 3 克砝码,在另一端放上 1 克的砝码;而要称出 7 克的物品,则可以在一端放上 1 克和 9 克的砝码,另一端放上 3 克的砝码。
类似地,要称出 1 克到 4 克中所有整数克的物品,只需要 2 个砝码;要称出 1 克到 13 克中所有整数克的物品,则只需要 3 个砝码;要称出 1 克到 121 克中所有整数克的物品则要 5 个砝码,它们分别是 1 克、3 克、9 克、27 克和 81 克,如此等等。
也许有人已经心领神会了,但是如果就此满足而匆匆离去的话,可能就错失了一个领略数学思想的机会——问题到这里并未结束啊!例如,4 个砝码究竟是不是最少的?还有没有其他的组合?对这些疑问的一个彻底的分析和说明,是 19 世纪由麦克马洪 (MacMahon) 给出的。下面就来领略一下其中的思想吧,或许你会从中学到很多。
因式分解的妙用
假设有一个重为 a 克的砝码,那么用它自然能够称出 0 克和 a 克的物品。不过,如果虚设天平的某一端为正的话,利用此天平和砝码我们还能称出 - a 克的物品——不妨规定把 a 克砝码放在天平右侧,将物品放在天平左侧,由此可以称出 a 克的物品;但若把 a 克砝码放在天平左侧,把物品放在天平右侧,由此称出的物品重量记作 - a。目前这样一种设想有点怪异,但这实际上和人类引入负数的思想是相同的。很快大家便会发现,这种设定非常精妙地简化了我们的计算和推导。现在暂且把该砝码能够称出的重量 - a,0,a 放进一个表达式中:
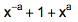
现在,假设有两个不同规格的砝码,分别重 a 克和 b 克(a
可以看到,它不是别的,正好是
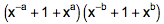
的展开式。
另外,假设有 m 个同样重为 a 克的砝码,则可以称出 - ma,- (m - 1)a,…,0,…,(m - 1)a,ma 克的物品。暂且按照上面的办法,把这些数也塞进一个表达式中 :

结合上面的分析,容易看出,如果有 m 个 a 克的砝码,n 个 b 克的砝码,等等,那么可以称出物品的克数就是表达式

展开后出现过的那些 x 的幂数,而展开式中 x 的 i 次项系数就表示用给定的这组砝码称出 i 克物品的不同方法数。
如果要称出 1 到 40 中所有的整克数,并且要求所用的砝码尽可能少,我们自然希望这些砝码能够“物尽其用”,称出的克数正好都是我们需要的克数,并且称的方法都是唯一的。也就是说,上述表达式展开后应该恰好是

反过来,就是要把

还原成

的形式。
对这个式子进行分解,一共有八种不同的方案:

前四个式子展示了我们实际上是如何对原式进行逐步分解的。它们的意义依次为:(1) 40 个 1 克的砝码;(2) 1 个 1 克,13 个 3 克的砝码 ;(3) 1 个 1 克,1 个 3 克以及 4 个 9 克的砝码;(4) 1 个 1 克,1 个 3 克,1 个 9 克以及 1 个 27 克的砝码。其中,第四个分解式是最基本的,它就是我们想要的答案。
当然我们还要说明,除了上面列举的 8 种组合之外没有其他的组合。这是一个多少有些复杂的讨论,不过我们可以就此为止了,因为上面的分解式看起来应该明显包含了所有可能的分解。最少的那组已经明摆着了,无须再说。大家可以到 死理性派小组 参与更详细的讨论
http://www.guokr.com/article/3742/



