OpenCV-Python系列之姿态估计

在上一节摄像机校准里，我们找到了摄像机矩阵，畸变参数等，给一个模板图像，我们可以用上面的信息来计算它的姿态，或者物体是如何处于空间中的，比如如何旋转的，怎么被移动的。对于一个平面物体。我们可以假设Z = 0，这样，问题现在变成了摄像机如何放置的来看我们的模板图像，所以，如果我们知道物体是怎么放在空间中的，我们可以画出2D图来模拟3D效果。

在计算机视觉中，物体的姿势指的是其相对于相机的相对取向和位置，一般用旋转矩阵、旋转向量、四元数或欧拉角表示（这四个量也可以互相转换）。一般而言，欧拉角可读性更好一些，也可以可视化（见下图，分别对应欧拉角的三个角度），所以常用欧拉角表示。欧拉角包含3个角度：pitch、yaw、roll，这三个角度也称为姿态角。

确定物体的姿态就是要计算其相对相机的欧拉角，刚提到也可以是旋转矩阵。旋转矩阵可以和欧拉角相互转换，一般而言，得到的欧拉角可以可视化到二维图像上，见下图。

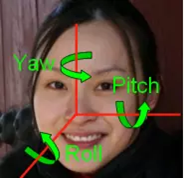
姿势估计问题通常称为Perspective-n-Point问题或计算机视觉术语中的PNP。在该问题中，目标是在我们有校准相机时找到物体的姿势或运动（即找到欧拉角或旋转矩阵），还需要知道物体上的n个3D点的位置以及相应的相机3D到图像2D平面的投影。

在上面的方程中，我们有很多已知的3D世界坐标点，即（U，V，W），但不知道具体的3D相机坐标（X，Y，Z），但知道3D相机坐标中的X和Y，即2D图像上的关键点。在没有径向畸变（即z点的畸变）的情况下，2D图像坐标中P点即（x，y）有以下公式。

下面公式描述了，将相机坐标（X，Y，Z）转换即投影为平面坐标（x，y，1）的过程，已知平面坐标和相机参数，通过下面公式算出相机坐标（X，Y，Z）：

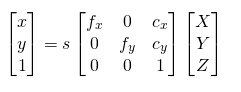
其中，f_x和f_y是在x和y方向上的焦距，并且（c_x，c_y）是光学中心。当涉及径向变形时，事情变得稍微复杂一些，为了简单起见不考虑这一项。

s是一个我们未知的比例因子，表示深度信息。举个例子，若将3D世界坐标中某个点P与3D相机坐标中对应的点P连接起来，即光线，那么这个光线会与图像平面相交得到二维平面上的点P。这个s就是这个过程中变换的深度信息，但我们这里因为未知，统统将所有点s考虑为一样的。

以下公式，将3D世界坐标（U，V，W）转换为3D相机坐标，已知3D世界坐标和上面公式算出的3D相机坐标，因而可以算出3x3的旋转矩阵和3x1的平移向量。

基于上面的两个公式，先用第一个公式计算出Z值，再用第二个公式计算出旋转矩阵，依次列出方程组，依次求解得到3D相机坐标的值Z、旋转R和平移T参数。这种方法称为直接线性变换（Direct Linear Transform，DLT）。

我们先来看代码：

import cv2
 import numpy as np
 import glob
 
 # Load previously saved data
 with np.load('B.npz') as X:
     mtx, dist, _, _ = [X[i] for i in ('mtx', 'dist', 'rvecs', 'tvecs')]

现在让我们创建函数，draw， 取棋盘的角点(用cv2.findChessboardCorners()）和坐标轴的点来画3d坐标轴

def draw(img, corners, imgpts):
     corner = tuple(corners[0].ravel())
     img = cv2.line(img, corner, tuple(imgpts[0].ravel()), (255,0,0), 5)
     img = cv2.line(img, corner, tuple(imgpts[1].ravel()), (0,255,0), 5)
     img = cv2.line(img, corner, tuple(imgpts[2].ravel()), (0,0,255), 5)
     return img

然后和前面的例子一样，我们创建结束条件，物体点(棋盘角的3D点）和坐标轴点，坐标轴点是在3D空间画坐标轴的。我们画长度为3的坐标轴（单位和棋盘面积大小相关）。所以我们的X轴从(0,0,0)画到(3,0,0)，同理可得Y轴。对于Z轴，从（0，0,0）画到(0,0,-3)。负数表明他是朝镜头画的。

criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
 objp = np.zeros((6*7, 3), np.float32)
 objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)
 axis = np.float32([[3,0,0], [0,3,0], [0,0,-3]]).reshape(-1,3)

现在，和平常一样，我们加载图像，搜索7x6网格，如果找到了，我们用子角像素改进一下它，然后计算旋转和平移，我们使用函数cv2.solvePnPRansac()。当我们计算完这些转换矩阵以后，我们用他们来投影我们的坐标轴点到图像平面上，简单的说，我们找到图像平面上的点对应3D空间里的(3,0,0), (0,3,0), (0,0,3)。当我们找到以后，我们就可以从第一个角到每个这些轴点画线，用draw()函数。解决！

for fname in glob.glob('left*.jpg'):     img = cv2.imread(fname)     gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)     ret, corners = cv2.findChessboardCorners(gray, (7,6),None)
    if ret == True:         corners2 = cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
        # Find the rotation and translation vectors.         rvecs, tvecs, inliers = cv2.solvePnPRansac(objp, corners2, mtx, dist)
        # project 3D points to image plane         imgpts, jac = cv2.projectPoints(axis, rvecs, tvecs, mtx, dist)
        img = draw(img,corners2,imgpts)         cv2.imshow('img',img)         k = cv2.waitKey(0) & 0xff         if k == 's':             cv2.imwrite(fname[:6]+'.png', img)
cv2.destroyAllWindows()

看下面的结果，注意每个坐标轴都是3格长：

渲染一个立方体

如果想要画䘝立方体，修改draw()函数和坐标轴点。

def draw(img, corners, imgpts):     imgpts = np.int32(imgpts).reshape(-1,2)
    # draw ground floor in green     img = cv2.drawContours(img, [imgpts[:4]],-1,(0,255,0),-3)
    # draw pillars in blue color     for i,j in zip(range(4),range(4,8)):         img = cv2.line(img, tuple(imgpts[i]), tuple(imgpts[j]),(255),3)
        # draw top layer in red color         img = cv2.drawContours(img, [imgpts[4:]],-1,(0,0,255),3)
        return img
修改坐标轴点，他们是立方体在3D空间里的8个角
axis = np.float32([[0,0,0], [0,3,0], [3,3,0], [3,0,0], [0,0,-3], [0,3,-3], [3,3,-3], [3,0,-3]])

结果：