主流排序算法全面解析
以下如无特殊说明都是按照升序进行排序。
源码见最下方
比较类排序
交换排序
冒泡排序
定义
是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端--维基百科。
思想
冒泡排序很简单，顾名思义每轮循环中将一个最大/最小的数通过交换一路冒到数组顶部。
代码
public class BubbleSort {
public static void main(String[] args) {
int[] arr = {4, 12, 2, 8, 453, 1, 59, 33};
for (int i = 0, length = arr.length; i < arr.length - 1; i++) {
for (int j = 0, tempLength = length - 1 - i; j < tempLength; j++) {
//如果当前数大于下一个数那么和下一个数交换位置
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
System.out.println(Arrays.toString(arr));
}
}
}
快速排序
定义
快速排序（Quicksort）是对冒泡排序的一种改进。由 C. A. R. Hoare 在 1960 年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列--百度百科。
思想
- 使用了分治的思想，先取一个数作为基数（一般选第一个数），然后将这个数移动到一个合适的位置使左边的都比它小，右边的都比他大
- 递归处理这个数左边的数和右边的数，直到所有的数都有序。直到所有的数都有序
代码
public class QuickSort {
private static void deal(Integer[] arr, int start, int end) {
if (start >= end) {
return;
}
int base = arr[start], i = start, j = end;
while (i < j) {
//在右边找一个比基数小的数,直到i,j相等
while (arr[j] >= base && j > i) {
j--;
}
//在左边找一个比基数大的数,直到i,j相等
while (arr[i] <= base && j > i) {
i++;
}
//如果ij不相等，交换其值
if (i < j) {
ArrayUtil.swap(arr, i++, j--);
}
}
//此时i等于j，交换基数和i/j,使左边的数小于等于基数，右边的数大于等于基数
if (start != i) {
ArrayUtil.swap(arr, start, i);
}
deal(arr, start, i - 1);
deal(arr, j + 1, end);
}
public static void main(String[] args) {
Integer[] arr = {1, 43, 2, 7, 5, 6, 555, 200, 21};
deal(arr, 0, arr.length - 1);
System.out.println("结果" + Arrays.toString(arr));
}
}
插入排序
简单插入排序
是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用 in-place 排序，因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间--维基百科。
思想
插入排序的思想很简单直接：
- 从第一个元素开始，该元素可以认为已经被排序
- 取出下一个元素，在已经排序的元素序列中从后向前扫描
- 如果该元素（已排序）大于新元素，将该元素移到下一位置
- 重复步骤 3，直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤 2~5
动图如下：
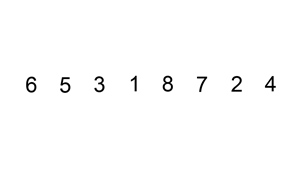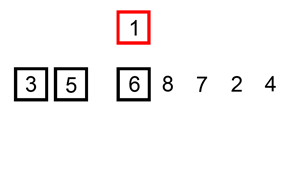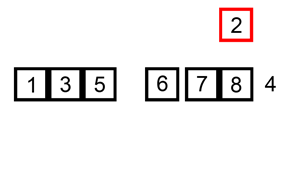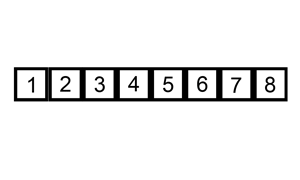
代码
public class InsertSort {
public static void sort(Integer[] arr) {
for (int i = 0, length = arr.length; i < length; i++) {
//有序部分从后向前比较,直到找到合适的位置
int j = i, temp = arr[i];
//如果arr[j-1]<=temp,说明arr[j]需为temp，否则将arr[j-1]向后移动一位
for (; j > 0 && temp < arr[j - 1]; j--) {
arr[j] = arr[j - 1];
}
arr[j] = temp;
System.out.println("当前数组状态为：" + Arrays.toString(arr));
}
}
public static void main(String[] args) {
Integer[] arr = {1, 65, 32, 12, 21};
InsertSort.sort(arr);
System.out.println(Arrays.toString(arr));
}
}
希尔排序
定义
希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的：
- 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率
- 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位
思想
- 取一个小于数组长度 n 的整数 n1，将所有间隔为 n1 的数分成一组，对各组进行直接插入排序.然后 n=n1；
- 重复上述操纵，直到 n1=1 进行一次完整的插入排序后结束。
代码
public class ShellSort {
public static void sort(Integer[] arr) {
int n1 = arr.length / 2;
// 也可将do/while替换成尾递归
do {
//共n1组数据需要进行直接插入排序
for (int start = 0; start < n1; start++) {
//对一组执行插入排序，第一个数为arr[start],增量为n1
for (int i = start; i < arr.length; i += n1) {
int j = i, temp = arr[i];
for (; j > start && temp < arr[j - n1]; j -= n1) {
arr[j] = arr[j - n1];
}
arr[j] = temp;
}
}
n1 /= 2;
} while (n1 >= 1);
}
public static void main(String[] args) {
Integer[] arr = {1, 65, 32, 12, 21};
ShellSort.sort(arr);
System.out.println(Arrays.toString(arr));
}
}
选择排序
简单选择排序
定义
是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
思想
简单选择排序顾名思义,每次从无序部分选出一个最大的数，和无序部分的最后一个值交换，重复 n-1 次后所有的值都变成有序状态.
动画如下：
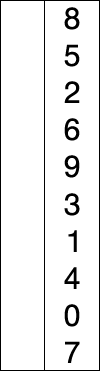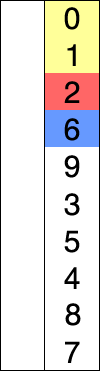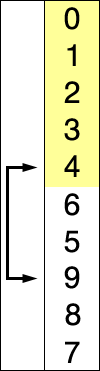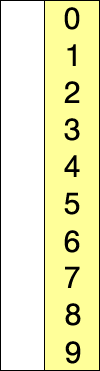
代码
public class SimpleSelectSort {
public static void sort(Integer[] arr) {
int length = arr.length;
for (int i = 0; i < length - 1; i++) {
int maxIndex = 0;
for (int j = 1; j < length - i; j++) {
if (arr[j] > arr[maxIndex]) {
maxIndex = j;
}
}
ArrayUtil.swap(arr, maxIndex, length - i);
}
}
public static void main(String[] args) {
Integer[] arr = {1, 65, 32, 12, 21};
sort(arr);
System.out.println(Arrays.toString(arr));
}
}
堆排序
定义
堆排序（英语：Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子节点的键值或索引总是小于（或者大于）它的父节点。
不了解堆的可以看看这篇，翻译的挺好的。
思想
- 构建大顶堆(升序用大顶堆，降序用小顶堆) ,i=arr.lengh-1,n=arr.lengh
- 将 arr[0]和 arr[i]互换,
- i--
- 重新将 arr 0 到 i 构建为大顶堆
- 重复 2，3，4 直到 i=1
构建大顶堆过程如下：
- 从最后一个非叶子节点开始从下往上进行调整。
- 将该节点的值调整为 max(节点值，直接子节点值），注意如果产生了交换操作还要调整被交换节点,让其也是 max（节点值，直接子节点值）,直到被交换节点无子节点
代码
public class HeapSort {
private static void sort(Integer[] arr) {
int n = arr.length;
//构建大顶堆
for (int i = n / 2 - 1; i >= 0; i--) {
adjustHeap(arr, i, n);
}
//排序
for (int i = n - 1; i > 0; i--) {
ArrayUtil.swap(arr, 0, arr[i]);
adjustHeap(arr, 0, i);
}
}
/**
* Description: 调整堆
*
* @param arr 数组
* @param index 调整index处的对结构
* @param length 堆大小
* @author fanxb
* @date 2019/7/31 19:50
*/
private static void adjustHeap(Integer[] arr, int index, int length) {
if (index >= length) {
return;
}
int maxIndex = index;
for (int i = 2 * index + 1; i < length - 1 && i <= 2 * index + 2; i++) {
if (arr[maxIndex] < arr[i]) {
maxIndex = i;
}
}
//如果进行了交换，还要调整被交换节点
if (maxIndex != index) {
ArrayUtil.swap(arr, maxIndex, index);
adjustHeap(arr, maxIndex, length);
}
}
public static void main(String[] args) {
Integer[] arr = {1, 65, 32, 334, 12, 21, 65, 112, 444443};
ShellSort.sort(arr);
System.out.println(Arrays.toString(arr));
}
}
归并排序
二路归并
定义
归并排序（英语：Merge sort，或 mergesort），是创建在归并操作上的一种有效的排序算法，效率为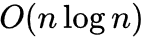
。1945 年由约翰·冯·诺伊曼首次提出。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。--维基百科
思想
归并排序的核心思想是将两个有序的数组合并成一个大的数组，这个过程称为 1 次归并。
一次归并过程如下(arr1,arr2 两个有序数组，arr3 存放排序后的数组,i=0,j=0,k=0)：
-
如果
arr1[i]<=arr2[j],那么arr3[k]=arr1[i]，i++,k++;否则arr3[k]=arr2[j]，j++,k++; -
重复 1，直到某个有序数组全部加入到 arr3 中，然后将另外一个数组剩余的部分加到 arr3 中即可。
但是一个无须数组显然不能直接拆成两个有序数组，这就需要用到分治的思想。将数组一层一层的拆分，直到单个数组的长度为 1（长度为 1 的数组可以认为是有序的），然后再反过来一层层进行归并操作，那么最后数组就变成有序的了。
排序过程动图如下(来自Swfung8)：
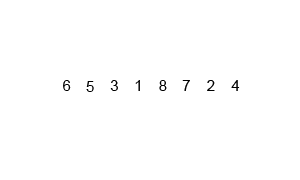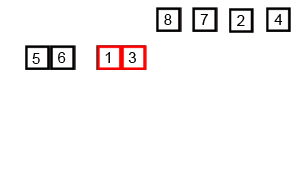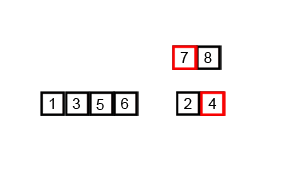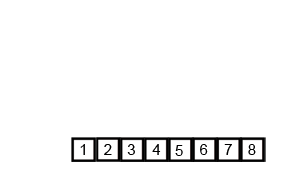
代码
public class MergeSort {
/**
* Description:
*
* @param arr 待排序数组
* @param start 开始下标
* @param end 结束下标
* @author fanxb
* @date 2019/8/6 9:29
*/
public static void mergeSort(Integer[] arr, int start, int end) {
if (start >= end) {
return;
}
int half = (start + end) / 2;
//归并左边
mergeSort(arr, start, half);
//归并右边
mergeSort(arr, half + 1, end);
//合并
merge(arr, start, half, end);
}
/**
* Description:
*
* @param arr arr
* @author fanxb
* @date 2019/8/5 17:36
*/
public static void merge(Integer[] arr, int start, int half, int end) {
ArrayList<Integer> tempList = new ArrayList<>();
int i = start, j = half + 1;
// 循环比较，将较小的放到tempList中
while (i <= half && j <= end) {
if (arr[i] <= arr[j]) {
tempList.add(arr[i]);
i++;
} else {
tempList.add(arr[j]);
j++;
}
}
if (i > half) {
//说明第一个数组已经完了，将第二个数组的剩余部分放到tempList中
while (j <= end) {
tempList.add(arr[j]);
j++;
}
} else {
//说明第二个数组已经完了，将第一个数组剩余部分放到tempList中
while (i <= half) {
//说明第二个数组处理完了
tempList.add(arr[i]);
i++;
}
}
//最后将tempList复制到arr中
for (int k = 0, length = tempList.size(); k < length; k++) {
arr[start + k] = tempList.get(k);
}
}
public static void main(String[] args) {
Integer[] arr = {4, 3, 1, 2, 5, 4, 2};
mergeSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
}
非比较排序
计数排序
定义
计数排序不以比较为基础，核心在于将数 a 存放在 arr[a]上,排序速度超级快，但是要求输入的数必须是有确定范围的整数。
思想
假设对于范围 0-100 的整数进行排序
- 定义长度为 101 的数组 arr,并将值初始化为 0
- 读取一个数 a，然后 arr[a]++
- 遍历 arr，数组上的每个值表示对应下标的数的出现次数。
代码
public class CountSort {
/**
* Description:
*
* @param arr 待排序数组
* @return void
* @author fanxb
* @date 2019/8/6 17:36
*/
public static void sort(Integer[] arr, Integer minValue, Integer maxValue) {
int range = maxValue - minValue + 1;
Integer[] numCount = new Integer[range];
Arrays.fill(numCount, 0);
for (Integer item : arr) {
item = item - minValue;
numCount[item]++;
}
int count = 0;
for (int i = 0; i < range; i++) {
if (numCount[i] == 0) {
continue;
}
for (int j = 0; j < numCount[i]; j++) {
arr[count] = minValue + i;
count++;
}
}
}
public static void main(String[] args) {
Integer[] arr = {1, 65, 32, 334, 12, 21, 65, 112, 444443};
sort(arr, 1, 444443);
System.out.println(Arrays.toString(arr));
}
}
PS
计数排序有很多的变种，下面列举几种：
- 存在负数怎么办?
很简单，先进行一次遍历将正数负数分开，在分别进行排序，负数取反后再排。
- 有空间限制且数组非常大怎么办？
这里可以利用文件来实现。先将超大的数组按照规则分成几个部分，分别存到文件中（比如 1-1000000 放在文件 1 中，1000001-2000000 放在文件 2 中，以此类推）就将超大的数组分成了小的数组，然后再分别计数排序即可。
基数排序
定义
是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。基数排序的发明可以追溯到 1887 年赫尔曼·何乐礼在打孔卡片制表机（Tabulation Machine）上的贡献。--来自维基百科
基数排序可以采用 LSD(从高位开始),MSD(从低位开始),这里以 MSD 为例。
（有兴趣的可以思考思考如何用 LSD 实现，目前网上绝大多数都是 MSD 实现的）
思想
- 先创建 10 个桶，分别对应数字 0-9。
- 从左往右取第一位的数字，放到对应的桶中
- 依次从桶中取出数字(要按照先进先出的原则)放到源数组中。
- 重复 2,3 步骤，依次对第二、第三。。。位的数字排序，直到最大位数处理完毕。
为什么能够这样排序呢？第一遍排序完毕后，所有的数是按照个位排序的，对于所有小于 10 的数来说，他们已经是相对有序(并不是说位置不再变化，只是相对顺序不再变化)的了，在第二轮对十位排序时，所有的个位数都将被放到 0 桶了，用先进先出策略处理这些个位数，取出时个位数还是有序的。
第二轮排序后所有小于 10 的数的位置已经确定且不再变化，大于 10 小于 100 的数的位置已经相对有序.在第三轮中所有小于 100 的数都将被放到 0 桶，这时相对有序就变成了绝对的了，取出后位置不再变化。
第三轮排序后所有小于 100 的数的位置已经确定且不再变化。以此类推直到全部排序完成。
动图如下：
代码
public class RadixSort {
@SuppressWarnings("unchecked")
public static void sort(Integer[] arr) {
//定义桶
LinkedList<Integer>[] buckets = new LinkedList[10];
for (int i = 0; i < 10; i++) {
buckets[i] = new LinkedList<>();
}
int size = arr.length;
//当前处理第几位的数
int count = 0;
while (true) {
//是否继续进位
boolean isContinue = false;
//将数放到桶中
for (int i = 0; i < size; i++) {
int temp = arr[i] / (int) Math.pow(10, count) % 10;
if (!isContinue && temp != 0) {
// 如果存在一个数取的值不为0，说明还要继续循环。
isContinue = true;
}
buckets[temp].addLast(arr[i]);
}
if (!isContinue) {
return;
}
//从桶中取出放到arr中,注意以什么顺序放进去的就要以什么顺序取出来（先进先出）
int index = 0;
for (int i = 0; i < 10; i++) {
Integer item;
while ((item = buckets[i].pollFirst()) != null) {
arr[index++] = item;
}
}
//位数+1
count++;
}
}
public static void main(String[] args) {
Integer[] arr = {4, 31, 1, 29, 5, 4, 2};
sort(arr);
System.out.println(Arrays.toString(arr));
}
}
源码:github
