相似度计算

 标量的计算

标量也就是无方向意义的数字，也叫标度变量。现在先考虑元素的所有特征属性都是标量的情况。

1.欧几里得距离

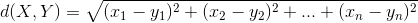
例如，计算X={2,1,102}和Y={1,3,2}

2.曼哈顿距离

 

3.闵可夫斯基距离

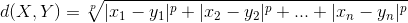
欧氏距离和曼哈顿距离可以看做是闵可夫斯基距离在p=2和p=1下的特例。

 

上面这样计算相异度的方式有一点问题，就是取值范围大的属性对距离的影响高于取值范围小的属性。例如上述例子中第三个属性的取值跨度远大于前两个，这样不利于真实反映真实的相异度，为了解决这个问题，一般要对属性值进行规格化。所谓规格化就是将各个属性值按比例映射到相同的取值区间，这样是为了平衡各个属性对距离的影响。通常将各个属性均映射到[0,1]区间，映射公式为：

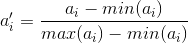
其中max(ai)和min(ai)表示所有元素项中第i个属性的最大值和最小值。例如，将示例中的元素规格化到[0,1]区间后，就变成了X’={1,0,1}，Y’={0,1,0}，重新计算欧氏距离约为1.732。