【转】K-Means聚类算法原理及实现

k-means 聚类算法原理：

  1、从包含多个数据点的数据集 D 中随机取 k 个点，作为 k 个簇的各自的中心。

  2、分别计算剩下的点到 k 个簇中心的相异度，将这些元素分别划归到相异度最低的簇。两个点之间的相异度大小采用欧氏距离公式衡量，对于两个点 T0(x1,y2)和 T1(x2,y2)，T0 和 T1 之间的欧氏距离为：

 

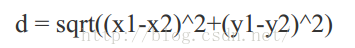
欧氏距离越小，说明相异度越小

  3、根据聚类结果，重新计算 k 个簇各自的中心，计算方法是取簇中所有点各自维度的算术平均数。

  4、将 D 中全部点按照新的中心重新聚类。

  5、重复第 4 步，直到聚类结果不再变化。

  6、将结果输出。

  举例说明, 假设包含 9 个点数据 D 如下(见 simple_k-means.txt), 从 D 中随机取 k 个元素，作为 k 个簇的各自的中心, 假设选 k=2, 即将如下的 9 个点聚类成两个类(cluster)

 

 

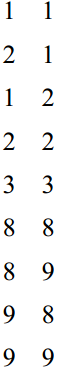
  1.假设选 C0(1 1)和 C1(2 1)前两个点作为两个类的簇心。
  2. 分别计算剩下的点到 k 个簇中心的相异度，将这些元素分别划归到相异度最低的簇。结果为:

 

  3.根据 2 的聚类结果，重新计算 k 个簇各自的中心，计算方法是取簇中所有元素各自维度的算术平均数。
C0 新的簇心为： 1.0,1.5
C1 新的簇心为： 5.857142857142857, 5.714285714285714
  4.将 D 中全部元素按照新的中心重新聚类。

 

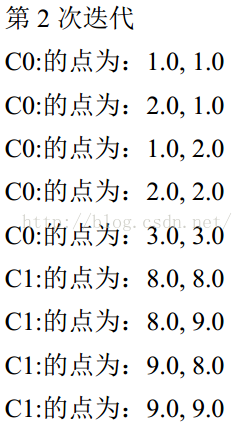
  5.重复第 4 步，直到聚类结果不再变化。当每个簇心点前后移动的距离小于某个阈值t的时候，就认为聚类已经结束了，不需要再迭代，这里的值选t=0.001，距离计算采用欧氏距离。
C0 的簇心为： 1.6666666666666667, 1.75
C1 的簇心为： 7.971428571428572, 7.942857142857143

 

 

C0 的簇心为： 1.777777777777778, 1.7916666666666667
C1 的簇心为： 8.394285714285715, 8.388571428571428

 

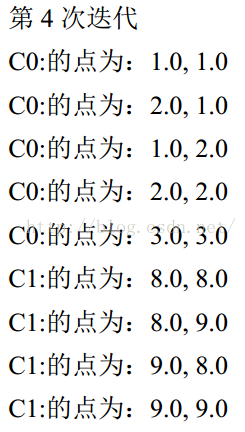
C0 的簇心为： 1.7962962962962965, 1.7986111111111114
C1 的簇心为： 8.478857142857143, 8.477714285714285

 

C0 的簇心为： 1.799382716049383, 1.7997685185185184
C1 的簇心为： 8.495771428571429, 8.495542857142857

 

C0 的簇心为： 1.7998971193415638, 1.7999614197530864
C1 的簇心为： 8.499154285714287, 8.499108571428572

#include <iostream>
#include <cstdlib>
#include <ctime>
#include <vector>
#include <cmath>
 
using namespace std;
 
class Cluster//聚类，每个聚类都包含两个属性，一个是簇心的属性（维数），另一个是距离本簇心最近的样本点
{
public:
    vector <double> centroid;//存放簇心的属性（维数）
    vector <int> samples;//存放属于相同簇心样本的下标
};
 
double CalculateDistance(vector<double> a, vector<double> b)//计算两个向量之间的距离
{
    int len1 = a.size();
    int len2 = b.size();
    if(len1 != len2)
        cerr<<"Dimensions of two vectors must be same!!\n";
    double temp = 0;
    for(int i = 0; i  < len1; ++i)
        temp += pow(a[i]-b[i], 2);
    return sqrt(temp);
}
 
//max_iteration表示最大的迭代次数，min_move_distance
vector<Cluster> KMeans(vector<vector<double> >data_set, int k, int max_iteration, double threshold)
{
    int row_number = data_set.size();//数据的个数
    int col_number = data_set[0].size();//每个向量(属性)的维数
 
    //初始随机选取k个质心
    vector<Cluster> cluster(k);//存放k个簇心。vector<T> v(n,i)形式，v包含n 个值为 i 的元素
    srand((int)time(0));
    for(int i = 0; i < k; ++i)
    {
        int c = rand()%row_number;
        cluster[i].centroid = data_set[c];//把第c个作为簇心，并把它相应的属性赋值给centroid
    }
 
    //iteration
    int iter = 0;
    while(iter < max_iteration)
    {
        iter++;
        for(int i = 0; i < k; ++i)
            cluster[i].samples.clear();
        //找出每个样本点所属的质心
        for(int i = 0; i < row_number; ++i)
        {
            double min_distance = INT_MAX;
            int index = 0;
            //计算离样本点i最近的质心
            for(int j = 0; j < k; ++j)
            {
                double temp_distance = CalculateDistance(data_set[i], cluster[j].centroid);
                if(min_distance > temp_distance)
                {
                    min_distance = temp_distance;
                    index = j;
                }
            }
            cluster[index].samples.push_back(i);//把第i个样本点放入，距离其最近的质心的samples
        }
 
        double max_move_distance = INT_MIN;
        //更新簇心
        for(int i = 0; i < k; ++i)
        {
            vector<double> temp_value(col_number, 0.0);
            for(int num = 0; num < cluster[i].samples.size(); ++num)//计算每个样本的属性之和
            {
                int temp_same = cluster[i].samples[num];
                for(int j = 0; j < col_number; ++j)
                    temp_value[j] += data_set[temp_same][j];
            }
            vector<double> temp_centroid = cluster[i].centroid;
            for(int j = 0; j < col_number; ++j)
                cluster[i].centroid[j] = temp_value[j]/cluster[i].samples.size();
            //计算从上一个簇心移动到当前新的簇心的距离
            double temp_distance = CalculateDistance(temp_centroid, cluster[i].centroid);
            if(max_move_distance < temp_distance)
                max_move_distance = temp_distance;
        }
        if(max_move_distance < threshold)
            break;
    }
    return cluster;
}
 
int main()
{
    int threshold = 0.001;//当从上一个簇心移动到当前粗心的距离几乎不变时，可以结束。这里用threshold作为阈值
    vector <vector<double> >data_set(9, vector<double>(2, 0.0));
    int point_number;
    cin>>point_number;
    for(int i = 0; i < point_number; ++i)
    {
        for(int j = 0; j < 2; ++j)
            cin>>data_set[i][j];
    }
 
    int col = data_set[0].size();
    vector<Cluster> cluster_res = KMeans(data_set, 2, 200, threshold);
    for(int i = 0; i < cluster_res.size(); ++i)
    {
        cout<<"Cluster "<<i<<" : "<<endl;
        cout<<"\t"<<"Centroid: ";//<<endl;
        cout<<"(";
        for(int j = 0; j < cluster_res[i].centroid.size()-1; ++j)
            cout<< cluster_res[i].centroid[j]<<",";
        cout<<cluster_res[i].centroid[cluster_res[i].centroid.size()-1]<<")"<<endl;
        cout<<"\t"<<"Samples: ";
        for(int j = 0; j < cluster_res[i].samples.size(); ++j)
        {
            int c = cluster_res[i].samples[j];
            cout<<"(";
            for(int m = 0; m < col-1; ++m)
                cout<<data_set[c][m]<<",";
            cout<<data_set[c][col-1]<<")  ";
        }
        cout<<endl;
    }
    return 0;
}
 
/**
1 1
2 1
1 2
2 2
3 3
8 8
8 9
9 8
9 9
*/

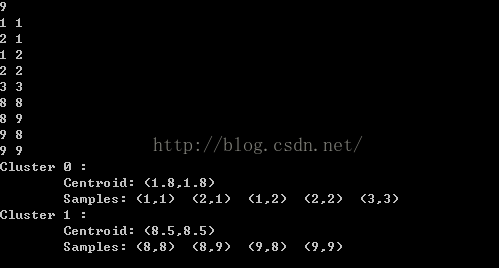
　　运行结果：

 

转发自：https://blog.csdn.net/hearthougan/article/details/52932452