第六章 模型的验证、监控与调优
模型的验证、监控与调优
简介:得到评分卡模型后,还需要验证模型的性能。并且部署后还要持续监测模型的表现。
目录:
- 模型的区分度
- 模型的预测性与混淆矩阵
- 模型的平稳性
- 模型的调优
- 模型的区分度
区分度的概念
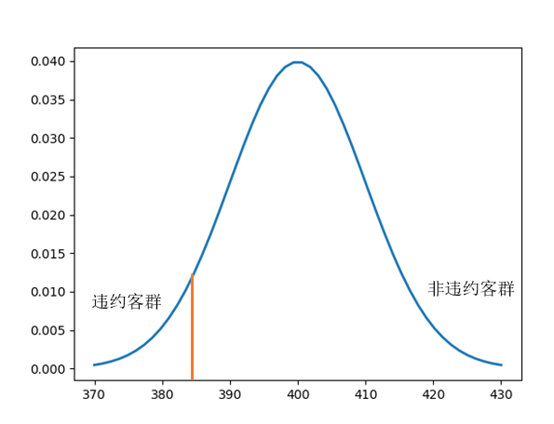
评分模型的作用是通过分数将好坏人群进行区分。从分数的性质可以看出,好的评分模型下违约人群的分数低、非违约人群的分数高。反之坏的评分模型下违约与非违约人群的分数是几乎无法区分的。在理想模型里,所有非违约人群的评分均高于违约人群。但在现实场景中无法达到这样的理想状态。因此我们需要借助某些统计量来衡量好坏人群分数的差异性,即评分模型的区分能力。
- 区分度的度量
从量化角度来说,我们需要找出一个指标来衡量分数对好坏样本的区分度,这样的一个指标需要满足一定的性质:
- 与区分能力单调相关,即指标越高(或越低)说明区分能力越强
- 与好坏样本的占比不相关。即在好、坏样本分层抽样的情况下依然不会发生显著的改变。例如,当好坏样本从100:1进行采样后变为10:1,度量指标依然不会发生显著的改变
一般可以从以下几个方面衡量模型的区分度:
- 好、坏样本的分布的差异
- 好、坏样本在统计学意义下的"距离"
- 从分布的差异性看区分度-KS值
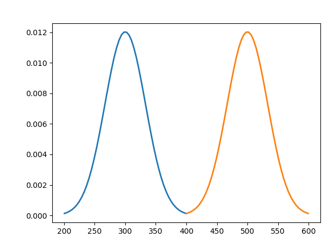
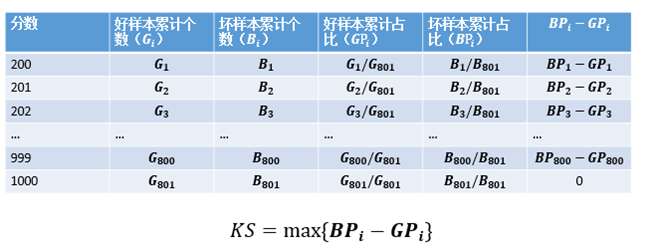
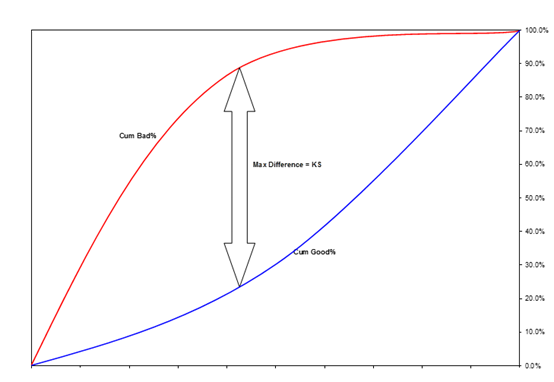
最直接的办法就是检验在评分的意义下两类样本的分布的差异性。在非参统计学里有多种指标可以计算两类样本的分布的差异性,最常用的就是KS(Kolmogorov-Smirnov)值。
分布的差异性看区分度-KS值(续)
需要注意的是,计算KS时需要将分数从低分到高分进行排序。这是因为评分模型中,违约人群的分数低于非违约人群。因此在低分段时,违约人群的累计速度会高于非违约人群。
正常情况下KS的范围是0~100%。当评分模型的结果与预期相反,即坏样本得分高于好样本时,KS为负。
KS越高,说明评分模型对好坏人群的区分能力越强。通常要求KS在训练样本上超过40%,在训练样本以及部署后超过30%。
KS对应的分数可以作为切分点(cut-off point)的选择之一。当两个模型在同一个样本集上的KS相等或者接近时,推荐使用切分点较小的模型。
- 从分布的差异性看区分度-Gini Score
除了KS值之外,还可以通过Gini Score来评估区分度:
先将样本分为若干组,再计算每组的坏样本率,进而得到Gini Score。Gini Score越小说明区分度越强。
需要注意的是:
- Gini Score与分组方式相关。同一个模型下,将样本分为10组与20组得到的结果是完全不同的。一般来说分组越细,Gini Score越小
- Gini Score不能反映分数在好坏人群上的有序性
- 对好坏比敏感。改变好坏比后,Gini Score也会发生改变。
- 从样本距离看区分度-散度(Divergence)
在机器学习模型和统计学模型中,"距离"是频繁使用的度量之一,用以衡量单个样本或者样本集的差异。同样的,在评分模型中我们也可以计算好坏样本的距离来检验分数的区分度:
和分别表示好坏样本的评分均值,和分别表示好坏样本的评分的方差。
注意:
- 与好坏样本的比例无关。当对好坏样本进行抽样处理后,不会显著影响到的值。
- 当好、坏样本的分数的分布比较接近正态分布时, 最能真实刻画区分度。
- 没有参照的阈值。可以用来比较不同模型在同一样本上的表现,或者同一模型在不同样本上的表现。
- 模型的预测性与混淆矩阵
模型的预测性
除了区分度之外,预测性也是评分模型重要的评估性能之一。与其他预测模型不用评分模型预测的准确性并不是简单地评估有多少样本能被正确地分类。
考虑以下场景:有1000个样本,其中有10个违约样本,其他都是非违约的。现在某模型将所有的样本都预测为非违约。在这样的情况下,分类正确率为(1000-10)/1000=99%.
从正确率的角度看,该模型的预测性是很强的。但是,该模型未能识别出任何一例违约样本,对信用风控是没有帮助的。我们需要寻找出可以正确评估模型预测性的指标。
两类错误
Type I:将好样本预测为坏样本
Type II:将坏样本预测为好样本
两类错误的代价是不同的。通常第二类错误的代价高于第一类。
- 混淆矩阵(confusion matrix)
在评分模型中,混淆矩阵及其衍生量是在二分类(或多分类)场景中常用的预测性能度量的工具。混淆矩阵的作用是细分了上一页陈述的两类错误。二分类下的混淆矩阵是:
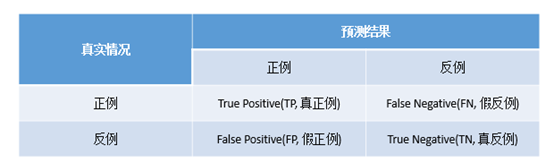
其中,对角线的值是预测正确的值;FP和FN表示第一类和第二类错误
在评分模型中,我们用正例代表违约类别,用反例代表非违约类别
- 混淆矩阵(续)
在混淆矩阵的基础之上,我们衍生出一些常用的性能指标
,所有被预测为违约的样本中,真正违约的比例
,所有真正违约的样本中,能被模型检测出来的比例
我们希望和都能达到很高的数值。但是在非理想的情况下,二者是不能同时增大的。例如,当我们认为所有的样本都是违约样本时,Recall达到最大,但是Precision很小。或者,当我们认为评分最低的那些样本是违约样本时,Precision很高但是Recall很小。
综合了Precision和Recall两个指标。
- ROC与AUC
但是上述的混淆矩阵是用于预测结果为类别的模型(例如SVM或者决策树)。评分模型的输出是分数(或概率,二者等价)。此时不能直接将输出结果用来构建混淆矩阵。解决办法是,先用分数与某一阈值做比较。低于阈值的样本被分为违约样本,反之则是非违约样本。任何一个阈值下都能建立相应的混淆矩阵,继而可以计算出Precision,Recall,F1或其他指标。将不同阈值下的性能指标用曲线图的方式展现出来是一个好的评估手段。ROC曲线是其中的一种常用的度量曲线,描述的是TPR和FPR在不同阈值下的变化情况。
FRP反映的是所有被预测为违约样本中,真实为非违约样本的比例。
类似的,我们希望TPR达到最大100%,同时FPR达到最小0%。此时意味着所有的违约样本都能被识别出来,而没有非违约样本被误判。但只有理想模型才能达到这种效果。
比较好的评分模型意味着当FPR较低时,TPR能相对达到比较大的值。反映在ROC曲线上,就是曲线尽可能的靠近(0,1)点。
坏的模型意味着好坏样本均匀散落在全部评分中,即TPR和FPR的增长速率相近。此时ROC曲线近似对角线。该模型近似随机判别的模型。
更坏的模型则将违约样本给予高分,将非违约样给予低分,此时ROC曲线低于对角线。
如何衡量ROC与(0,1)接近的程度呢?曲线下的面积是较好的度量工具。该面积被称为AUC(Area Under Curve)。当AUC较大时,说明模型的预测能力很强。通常用70%作为评估AUC的阈值。

- 模型的预测性和区分性的总结
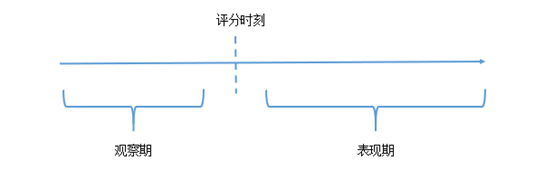
需要注意的是,在衡量模型的预测性和区分性的时候,需要知道样本的违约标签,意味着需要等待一个完整的表现期。如果表现期定位1年,则现在只能衡量模型在1年前的预测性和区分性。
- 模型的平稳性
- 平稳性
评分模型追求平稳性,即当信贷产品、客群、宏观经济、监管政策等没有发生大的变化时,在不同客群或者相同客群不同时间上的评分的结果应该相对保持稳定。由于评分卡模型的入模变量已经经过分箱处理,消除了有细微的变化对评分结果带来的影响,因此"随机性"的因素已经得到了一定的控制。在这样的情况下,如果评分结果发生较激烈的变化,说明模型的平稳性发生弱化。
在评分模型中,通常用PSI指标来衡量模型的平稳性。计算如下:
同一个评分模型在两份样本(比如,同一个信贷产品在不同月份的申请人群的得分)上比较分布的平稳性。将两份样本分各自为K组,计算每组在各自总体中的比例,设为。
PSI越低说明两组样本上的分数越接近。
注:
- 常用的阈值为25%。高于25%说明模型的平稳性发生弱化。
- PSI同时也受到分组方式的影响。一般来说分地越细,PSI越低。
- PSI的计算与好、坏标签无关,因此不需要积累一个完整的表现期。
4.模型的调优
- 模型调优的必要性
模型需要进行必要的调优,当遇到如下情形时:
1,监控结果不满足要求
- 连续3个月的KS低于30%,AUC低于70%,PSI高于25%
2,产品发生变化
- 额度提高,周期提高,利率降低
3,人群发生变化
- 准入政策发生变化
4,其他宏观因素发生变化
- 特征层面的调整
特征层面的调整通常分为2种:
1,舍弃或者新增特征
例如:舍弃"过去6个月的跨银行申请次数",新增"过去3个月的跨银行申请次数"
2,调整特征计算方法或者分箱方法
例如:对年龄进行重新分箱
调整的原则是:
当变量的PSI显著升高,或者IV显著降低时,需要做调整
- 分数层面的调整
根据新的样本和(或)调整后的特征,重新进行模型训练,估计模型参数
要求:
- 新模型的KS、AUC等指标不低于原有模型以及30%和70%的标准
- PSI不高于原有模型以及25%的标准


