第五章 逻辑回归模型在评分卡开发中的应用
逻辑回归模型在评分卡开发中的应用
课程简介:在分类场景中,逻辑回归模型是常用的一类算法。它具有结构简单、可解释性强、输出结果是"软分类"的特点。评分模型多采用这类算法。同时逻辑回归模型也面临一些限制,因此在特征工程阶段我们对输入特征做了相应的调整和约束。
目录:
- 逻辑回归模型的基本概念
- 基于逻辑回归模型的评分卡构建工作
- 尺度化
1. 逻辑回归模型的基本概念
- 伯努利概型
在分类模型中,目标变量是离散、无序型的变量。例如,违约预测模型中的目标变量(也称为标签)是{违约,非违约}。线性回归模型无法对这类标签进行建模,因为线性回归模型的结果的取值空间是整个实数空间.对于分类模型而言,我们建模的对象是每个类别在某条样本上出现的概率。
伯努利概型
某个事件有"发生"与"不发生"两种互斥的状态。假设该事件发生的概率为,不发生的概率即为.我们用1和0表示事件的发生与不发生,则有:
可以统一成
逻辑回归模型与logistic变换
在违约预测场景中,单个个体的违约事件可以看成伯努利概型:
参数即是我们需要预测的目标。
如果对概率做拟合?
概率的取值范围是0~1.如前所述,线性回归的目标变量的取值空间是整个实数空间,因此不适合用线性回归模型做预测。引入下面的logistic变换(也称为sigmoid函数),能够是的拟合的目标函数的取值范围限定在0~1:
逻辑回归模型与logistic变换(续)
的特点
- 单调性,即>
- 有界性,即
- 可导性,即
除此之外,还有一个计算上的优势,即
- 逻辑回归模型与logistic变换(续)
由于logistic变换有上述种种优点,我们将该变换应用在概率的刻画当中:
其中分别表示第i个观测值上p个特征的取值和特征的权重。
于是整个逻辑回归模型的形式为:
需要注意的是,这里的回归模型是对违约概率做回归,而非对违约结果{0,1}做回归。
- 参数估计
通常用极大似然估计法(MLE)求出逻辑回归的参数
对于样本,逻辑回归模型的似然函和对数似然函数分别为
参数估计的结果是为了让似然函数最大化。由于对数似然函数与似然函数单调上升且具有更紧凑的形式,同时也易于求导运算,因此将似然函数最大化转化为对数似然函数最大化,即
对求偏导,结果是
显然,的方程是没有解析解的。
无法得到解析解的情况下,只能通过数值求解的方式来计算参数的估计。常用梯度上升法来迭代地计算。基本的算法步骤如下:
- 初设化参数和步长
- 计算当前梯度:
- 更新参数:
- 直至满足终止条件
注:
根据计算梯度使用的样本量的多少,梯度上升法分为批量梯度上升法、随机梯度上升法与小批量梯度上升法。
- 逻辑回归模型的优点
结构简单:
- 变量之间的关系是线性可加关系
可解释性高:
- 结构简单;输入变量对目标变量的影响是容易获得的
支持增量训练:
- 无需读入全部数据,可增量式地读取数据、训练模型
给出概率而非判别类别:
- 模型的结果是估计出属于某一类的概率,可用于更加复杂的决策
工程化相对容易:
- 模型的测试、部署、监控、调优等工作相对简单
逻辑回归模型的不足
预测精度一般
- 由于模型结构较为简单,导致预测精度不如其他模型
对变量要求高
- 输入变量需数值类型,需要对非数值变量进行编码
- 不能容忍缺失值,需要对缺失值做处理
- 对异常值敏感,需要对异常值做处理
- 变量尺度差异较大时,容易对模型有影响,需要做变量归一化
- 变量间的线性相关性对模型有影响,需要做变量挑选或加上正则项
2.基于LR模型的评分卡构建工作
逻辑回归模型对变量的要求
当用逻辑回归模型来构建评分卡时,入模变量需要满足以下条件
- 变量间不存在较强的线性相关性和多重共线性
- 变量具有显著性
- 变量具有合理的业务含义,即变量对于风控业务是正确的
其中,第1点已经在单变量分析与多变量分析中得到一定的约束,但是未必充分。
关于第2点,需要从系数的p值进行检验
关于第3点,需要从系数的符号进行检验
- 变量显著性
为了获取与目标变量(即违约标签)有较高相关性的变量,我们要求最终入模的变量的系数的p值很小,例如低于0.1。如果发现模型中某些变量不显著,需要检验一下两种可能性:
- 该变量本身不显著
- 该变量显著,但是由于有一定的线性相关性或者多重共线性,导致该变量在多元回归下不显著
先检验1的可能性,如果排除,再检验2.
检验1的方法:
将该变量单独与目标变量做逻辑回归模型,如果在单变量回归的情况下系数的p值仍然较高,即表明该变量本身的显著性很低。
注:
对于IV较高的变量,1的可能性较低。
- 变量正确性
在WOE的计算公式中,
当WOE为负时,表明当前箱的"危险性"高于平均样本的"危险性",出现坏样本的概率更高。因此在逻辑回归模型中,所有变量对应的系数应该为负。
反之,如果采取的WOE的计算公式为:
同理,所有变量对应的系数应该为正。
- 逻辑回归模型对变量的要求(续)
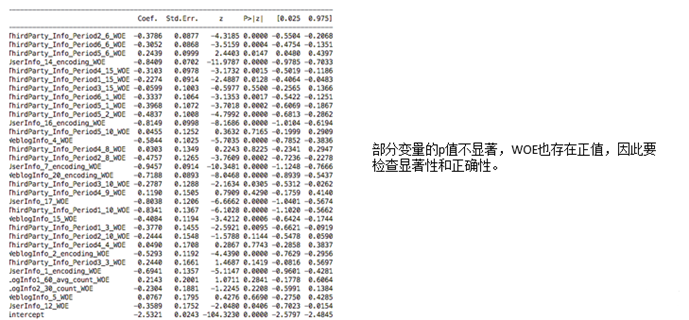
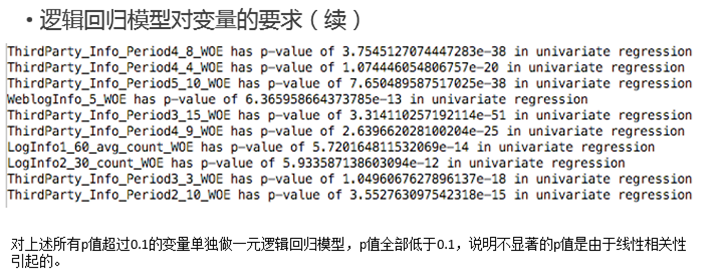
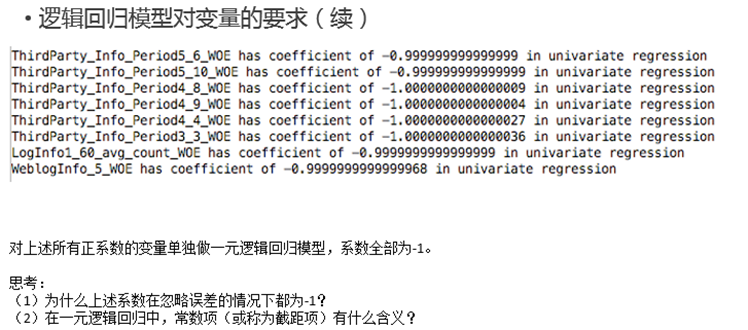
- 特征选择
从上述的单变量回归中可以发现,在full regression中,不显著、不正确的变量是由于线性相关性引起的。因此需要在做一次变量挑选。变量挑选的目的是为了满足:
- 入模变量正确并且显著
- 入模变量的"重要性"是最高的
其中,我们可以用IV来衡量入模变量的重要性。
综上,变量挑选的步骤如下:
- 将变量根据IV进行降序排列,不妨设为,其中""代表重要性的次序
- 当前的入模变量集合为{}
- 从剩余的变量中挑选第一个变量放入上一步的集合中,建立回归模型。如果该模型的所有的变量都满足p值小于阈值、系数为负,则在入模变量集合中保留该变量,否则剔除
- 遍历所有变量
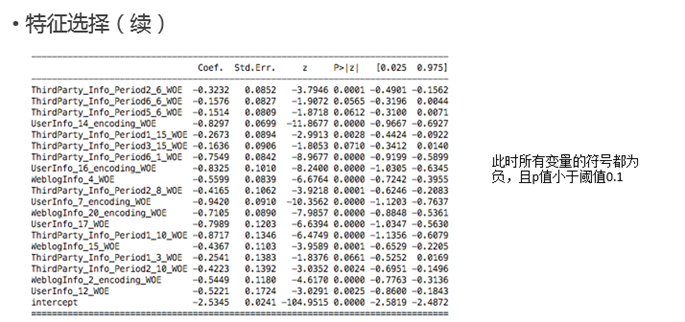
- 尺度化
得到符合要求的逻辑回归模型后,通常还需要将概率转化成分数。分数的单调性与概率相反,即分数越高表明违约的概率越低,信用资质越好。在评分卡模型中,上述过程称为"尺度化",转换公式为:
其中,, : point to double odds
PDO的作用
假设当前的好坏比为, 对应的分数为.
当好坏比上升一倍时变为2, 即=y-ln2, 此时分数变为
因此,PDO的含义即为,当好坏比上升1倍时,分数上升PDO个单位。
Base Point的选择
要满足所有的评分的取值为正。