第三章 数据的预处理与特征构建
申请评分卡模型
数据的预处理与特征构建
简介:在构建评分卡模型的工作中,数据的预处理和特征构建工作是至关重要的一步。数据的预处理工作可以有效处理缺失值与异常值,从而增强模型的稳健性。而特征构建工作则可以将信息从字段中加以提炼,形成有业务含义的优异特征。
- 评分卡模型的简介
风控场景中的评分卡:
- 以分数形式来衡量风险几率的一种手段
- 是对未来一段时间内违约/逾期/失联概率的预测
- 有一个明确的(正)区间
- 通常分数越高越安全
- 数据驱动
- 反欺诈评分卡、申请评分卡、行为评分卡、催收评分卡
非信贷场景中的评分卡:
- 推荐评分卡
- 流失评分卡
常用的信贷评分卡:
申请评分卡(Application Scorecard)
用在贷前审核环节,评估房贷后是否会违约的模型。常用特征:个人信息、央行征信信息、申请行为信息、其他辅助信息
行为评分卡(Behavioral Scorecard)
用在贷后监控环节,做早期预警的工作(包括巴塞尔2.5及之前AIRB的要求),常用特征:贷后还款行为、消费行为等。通常适用于还款周期长的产品或者循环授信类产品
催收评分卡(Collection Scorecard)
用在发生逾期后的管理环节,为催收工作提供指导。催收评分卡又可细分为预测失联的失联评分卡、预测逾期加重的滚动率评分卡和预测催收后的还款率的还款评分卡。常用特征:个人信息、贷后的还款行为、消费行为、联系人信息等。
评分卡模型开发步骤:
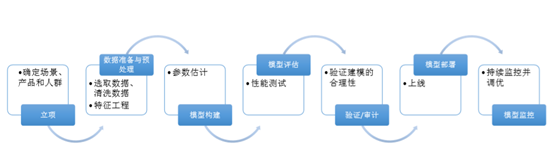
• 评分卡开发的常用模型
逻辑回归
优点: 简单,稳定,可解释,技术成熟,易于监测和部署
缺点:准确度不高
决策树
优点: 对数据质量要求低,易解释
缺点:准确度不高
其他元模型
组合模型
优点: 准确度高,不易过拟合
缺点:不易解释;部署困难;计算量大
- 数据集介绍
本次案例分析用的数据,是拍拍贷发起的一次不信贷申请审核工作相关的竞赛数据集。其中共有3份文件:
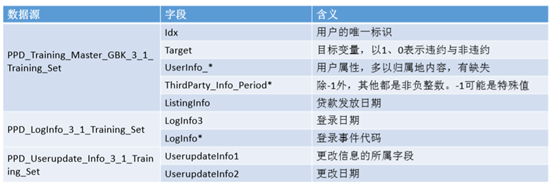
PPD_Training_Master_GBK_3_1_Training_Set.csv:信贷客户在拍拍贷上的申报信息和部分三方数据信息,以及需要预测的目标变量
PPD_LogInfo_3_1_Training_Set.csv:信贷客户的登彔信息
PPD_Userupdate_Info_3_1_Training_Set.csv:部分客户的信息修改行为
建模工作就是从上述三个文件中对数据进行加工,提取特征幵建立合适的模型,对贷后表现做预测
关键字段:
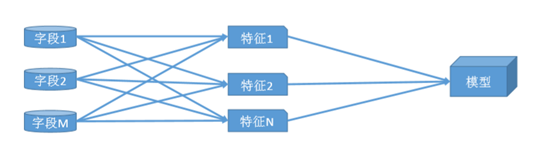
- 特征构造的方法
在评分卡模型的开发中,特征构造是极其关键的步骤,其作用是将分散在不同字段中的信息加以组合, 从中提炼出有价值的、可用的信息进而进行评分卡模型的开发。
部分常用的特征构方法有:
求和:例如过去一段时间内的每月网购金额的总和
比例:例如申请贷款的月还款本息不月收入的占比
频率:例如过去一段时间内的境外消费次数
平均:例如过去一段时间内平均每次信用卡取现额度
好的特征需要具备以下优势
稳定性高:当人群分布稳定、产品营销稳定、宏观经济因素稳定、监管 政策稳定时,特征的分布也需要稳定
区分度高:未来的违约与非违约人群在特征上的分布需要显著不同
差异性大:不能对全部人群或绝大部分人群上有单一的取值
复合业务逻辑:特征与信用风险的关联关系要符合风控业务逻辑
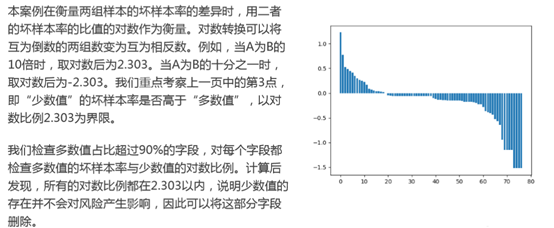
案例:对PPD_LogInfo_3_1_Training_Set字段的处理
在该数据源中,我们有代表身份的idx、代表登彔日期的LogInfo3和操作代码LogInfo1不LogInfo2。 计算登彔日期不放款日期乊间的间隔天数,可以看到绝大部分的天数在180天以内.

由于绝大部分观测样本的时间跨度在半年内,所以我们选取半年内的时间切片,考虑以月为单位的时间切片,则可以衍生出30天、60天、90天、120天、150天、180天等多种选择。
同时,对于类别型变量,可以考虑构造如下计算逻辑:
时间切片内的登录的次数
时间切片内不同的登录方式的个数
时间切片内不同登录方式的平均个数
不同的时间切片与不同的计算逻辑的交互可以产生多个特征。这些特征往往存在一定程度上的线性相关性。在接下来的多变量分析中,需要消除线性相关性对模型产生的影响。
注意:
该数据源中,每个idx存在多条记彔。上述的特征构造是针对每个idx进行相应的计算
4.数据的质量检验与处理
数据的质量检验-数据集中度

• 数据的质量检验-数据缺失(data missing)
数据缺失度是数据质量检验的一个重要项。需要从两个维度检验数据缺失度:
1)字段维度,即某个字段在全部样本上的缺失值个数的占比
2)样本维度,即某条样本在所有字段上的缺失值的占比
一般而言,字段维度的缺失程度会大于样本维度的缺失程度
• 缺失值处理
舍弃该字段或该条记彔:缺失占比太高
补缺:缺失占比不高,可用均值法、众数法、回归法等
作为特殊值:将缺失看成一种特殊值
其中,补缺的方法依变量类型的不同而有所差异。比如,均值法和回归法适用于数值型变量,众数法 适用于类别型变量。我们需要分辨出变量是属于类别型还是数值型。在实际业务中可按照下述的准则来判断变量的类型:
• 当且仅当变量取值为数值,且不同值的个数比较多时,视为数值型变量,这时可以用均值法(完全 随机缺失)、抽样法(完全随机缺失)、回归法(针对随机缺失)进行补缺
• 其他情况下均视为类别型变量,这时可以用抽样法、众数法进行补缺。
补缺工作的前提是,字段整体的缺失率不宜太高,否则会产生较大的偏差且对字段的使用(包括由该字段衍生的特征)的使用效果产生影响。
在信贷评分模型中,数据的缺失包含着多重意义。很多时候是完全非随机缺失,其缺失状态有着业务含义。例如,某些信贷产品的申请环节需要提供芝麻分,而且该字段的缺失本身对应的风险就比较高。 有些时候缺失是完全随机缺失,缺失与否并不影响信用风险。对于不同的缺失机制,对应的处理方法也有所不同。
• 完全非随机缺失:有缺失值的样本的违约率显著高于无缺失样本,此时应当将缺失当成一种特殊的状态
• 完全随机缺失:有缺失值的样本的违约率不无缺失样本无明显差异,此时如果缺失样本的占比很少,可将样本删除。如果缺失样本的占比较高,需要将字段删除。
数据的质量检验-异常值(outliers)

但是在信用评分模型中,异常值往往也带有特殊的意义,例如,在提交的申请资料中,如果PBOC征信记彔查询次数过多,可能该申请人在一定时间内申请贷款的次数过多,则很有可能该申请人面临的资金需求很迫切,对未来的逾期概率产生不好的影响。对于这部分人,在数据预处理阶段是不宜直接 删除戒者用正常值进行替换。评分卡模型的开发中,也有相应的方法来处理这样的异常值
数据的质量检验-数据含义一致性
在实际工作中,数据的彔入中往往会使得原本属于同一含义的记彔值出现不同的记彔。例如,通讯方式"QQ"与"qq"是一类性质,或者手机号码"+8613000000000"不"13000000000"均表示 同一个号码。因此,我们需要将具有相同含义的数据进行统一。
本案例中,需要手劢地将"QQ" 和" qQ", "Idnumber" 和" idNumber"以及 "MOBILEPHONE"和"PHONE"进行统一


