第12章 决策树

什么是决策树：

，

 

 

 ，

 

 

 ，

 

 ，

 

 

 ，

 

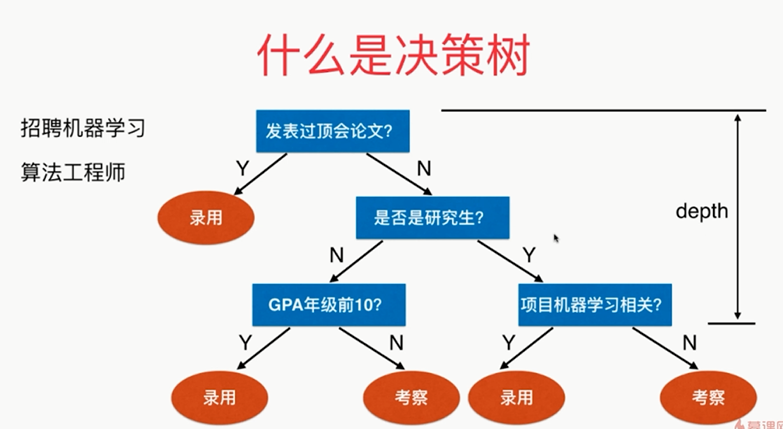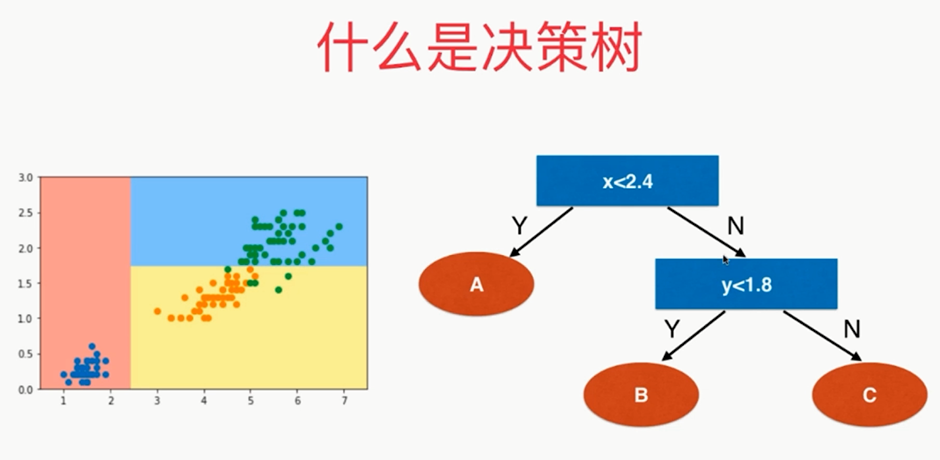
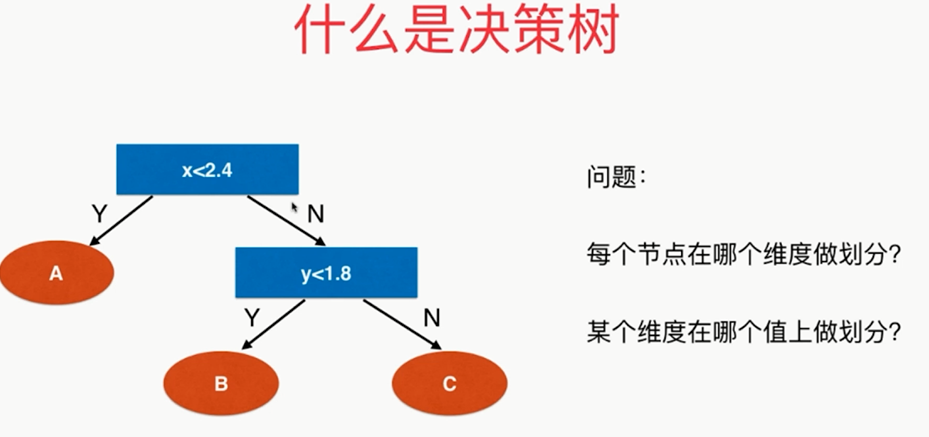
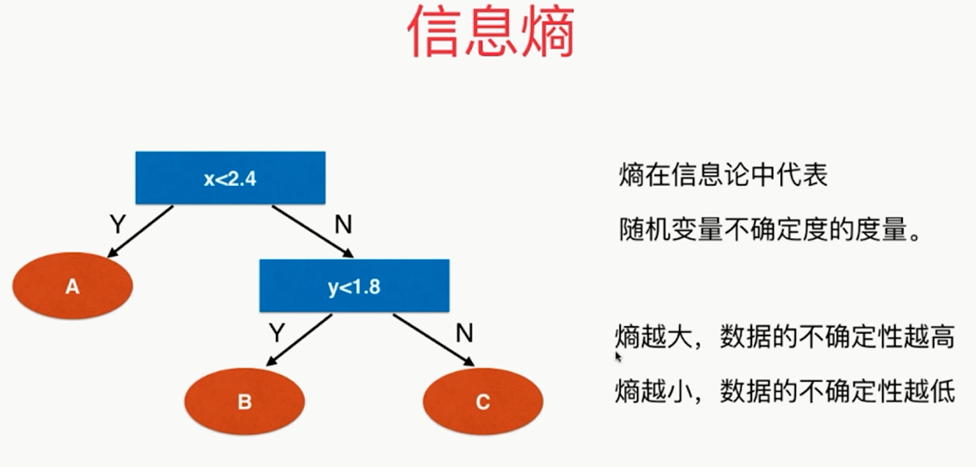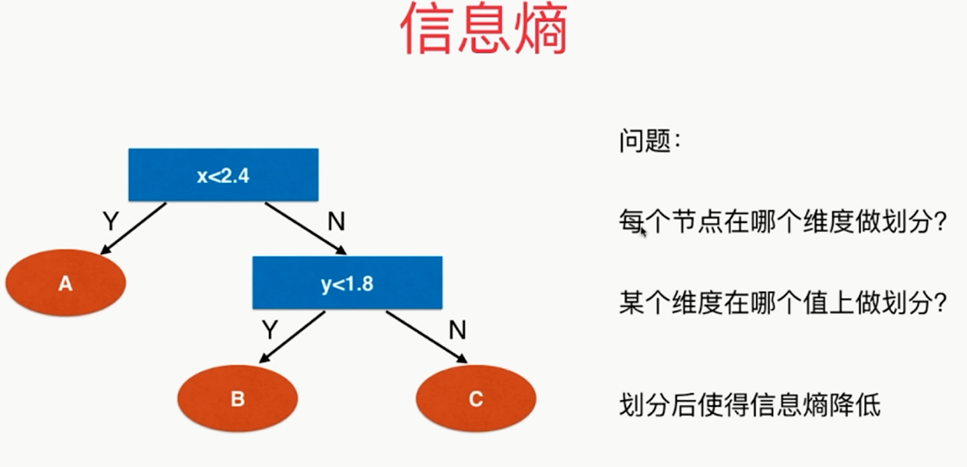朝着信息熵降低的方向，即让系统变得更加确定

 

 

def split(X,y,d,value):  # 每个节点上的维度d，相应的阈值：value
    index_a=(X[:,d]<=value)
    index_b=(X[:,d]>value)
    return X[index_a],X[index_b],y[index_a],y[index_b]

from collections import Counter
from math import log


def entropy(y):
    counter = Counter(y)
    res = 0.0
    for num in counter.values():
        p = num / len(y)
        res += -p * log(p)
    return res


def try_split(X, y):
    best_entropy = float('inf')
    best_d, best_v = -1, -1
    for d in range(X.shape[1]):  # shape[0]代表有多少行，shape[1]代表有多少列
        sorted_index = np.argsort(X[:, d])
        for i in range(1, len(X)):
            if X[sorted_index[i - 1], d] != X[sorted_index[i], d]:
                v = (X[sorted_index[i - 1], d] + X[sorted_index[i], d]) / 2
            X_l, X_r, y_l, y_r = split(X, y, d, v)
            e = entropy(y_l) + entropy(y_r)
            if e < best_entropy:
                best_entropy, best_d, best_v = e, d, v
    return best_entropy, best_d, best_v

best_entropy, best_d, best_v=try_split(X,y)
print("best_entropy=",best_entropy)
print("best_d=",best_d)
print("best_v=",best_v)

 

 基尼系数：越高数据的不确定性越强，和信息熵类似

，

 

 

按二分类 的思想：一类是x，另一类是（1-x）

此时：

 ，

 

 scikit-learn中默认使用基尼系数！

，

 

 

 ，

 

 

 

 ，

 

 

 

 

 ，

 

 

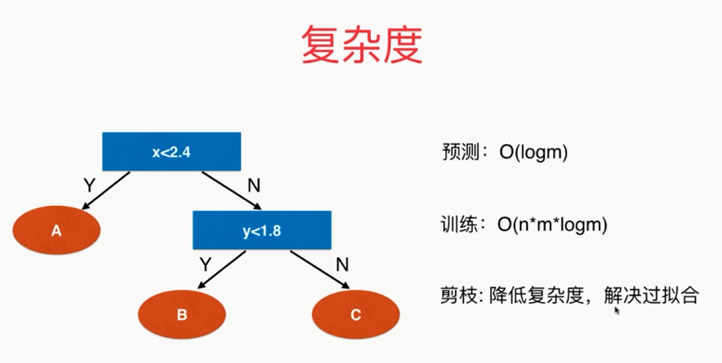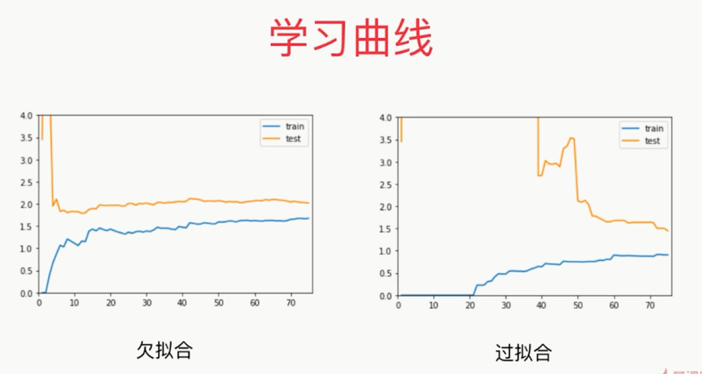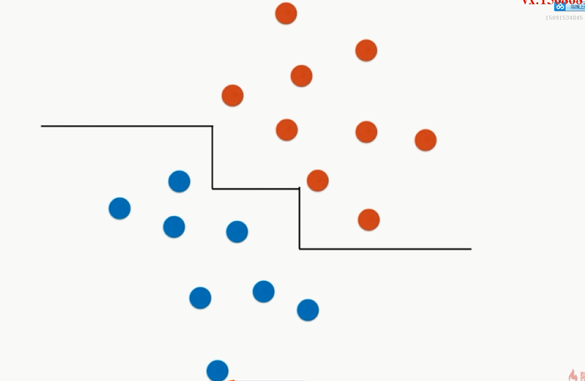
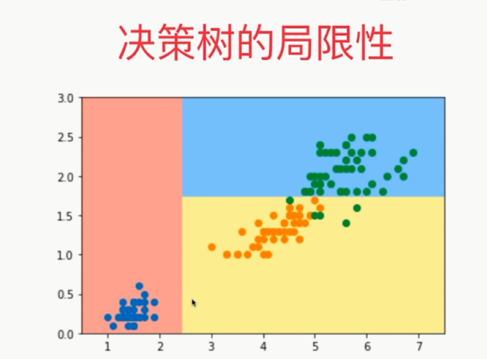
局限性：决策边界和坐标轴平行，导致决策边界成了这样

 

 

 而真正合理的是这样的：

 

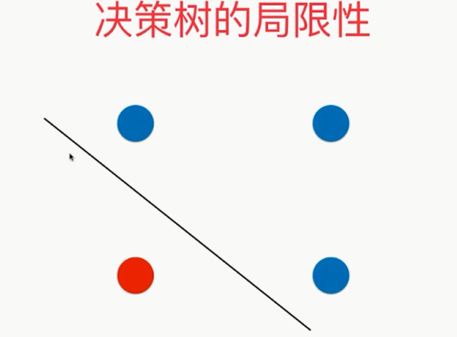
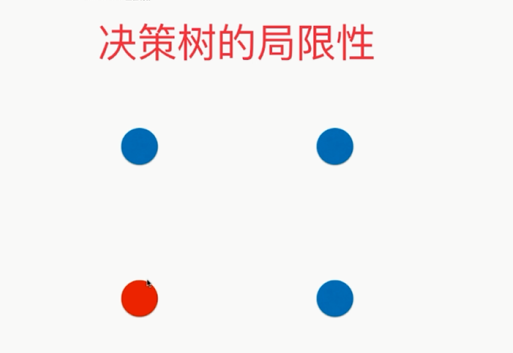
更严重的是：

，
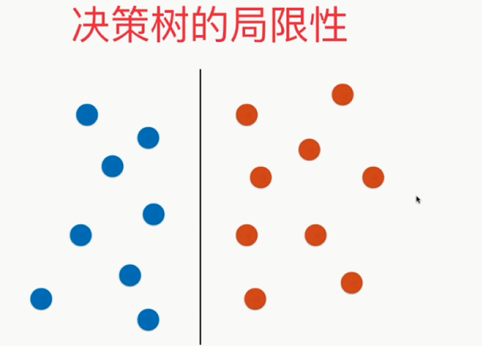