软件测试homework 3

1. 基于Junit 及Eclemma （jacoco ）实现一个主路径覆盖的测试

package cn.scs.st;

public class PrintPrime {
    public static String printPrimes (int n) 
    { 
        int MAXPRIMES = 10;
        int curPrime; // Value currently considered for primeness 
        int numPrimes; // Number of primes found so far. 
        boolean isPrime; // Is curPrime prime? 
        int [] primes = new int [MAXPRIMES]; // The list of prime numbers. 
        // Initialize 2 into the list of primes. 
        primes [0] = 2; 
        numPrimes = 1; 
        curPrime = 2; 
        while (numPrimes < n) 
        { 
            curPrime++; // next number to consider ... 
            isPrime = true; 
            for (int i = 0; i <= numPrimes-1; i++) 
            { // for each previous prime. 
                if (curPrime%primes[i]==0) 
                { // Found a divisor, curPrime is not prime. 
                    isPrime = false; 
                    break; // out of loop through primes. 
                } 
            } 
            if (isPrime) 
            { // save it! 
                primes[numPrimes] = curPrime; 
                numPrimes++; 
            } 
        } // End while 

        // Print all the primes out. 
        String s = null;
        for (int i = 0; i <= numPrimes-1; i++) 
        { 
            System.out.println ("Prime: " + primes[i]); 
            s += primes[i];
        } 
        return s;
    } // end printPrimes
    
    
}

全覆盖测试

package cn.scs.test;

import static org.junit.Assert.*;

import org.junit.Before;
import org.junit.Test;

import cn.scs.st.PrintPrime;

public class test {
    public PrintPrime prime;
    
    @Before
    public void setUp(){
        prime = new PrintPrime();
    }
    
    @Test
    public void testCase(){
        
        assertEquals("null235711", prime.printPrimes(5));
    }


}

测试结果

 

2. Use the following method printPrimes() for questions a–d.

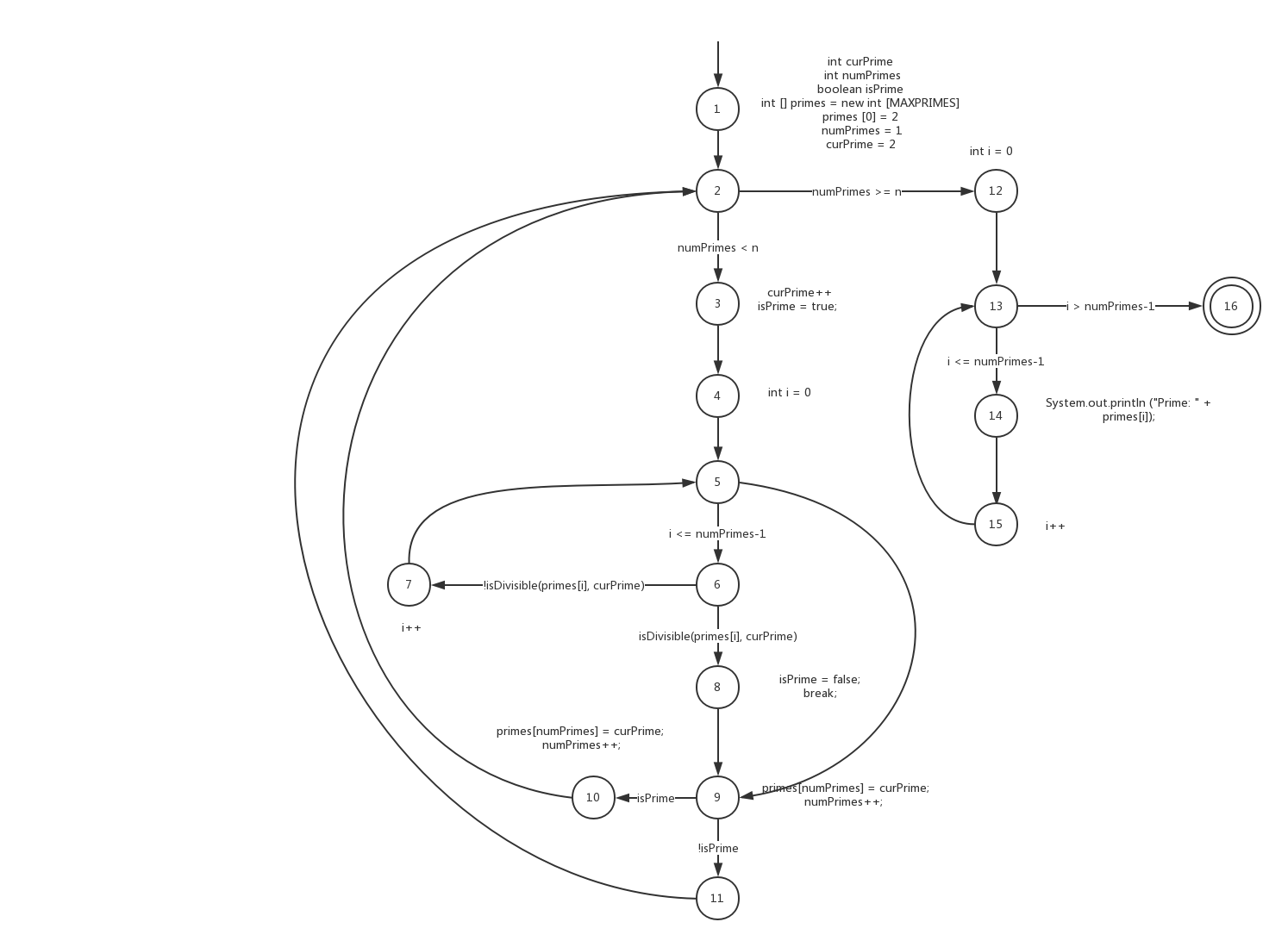
b. 将MAXPRIMES设为4，这样t2=(n=5)就会出现数组越界的错误，但t1=(n=3)无影响。

c. 当n=1的时候，不满足numPrime < n, 不会执行循环

d.

点覆盖

{ 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}

边覆盖

{(1,2),(2,3),(2,12)(3,4),(4,5),(5,6),(5,9),(6,7),(6,8),(7,5),(8,9),(9,10),(9,11),(10,2),(11,2),(12,13),(13,14),(13,16),(14,15),(15,13)}

主路径覆盖

{(1,2,3,4,5,6,7),

(1,2,3,4,5,9,10),

(1,2,3,4,5,9,11),

(1,2,3,4,5,6,8,9,10),

(1,2,3,4,5,6,8,9,11),

(1,2,12,13,14,15)

(1,2,12,13,16),

(2,3,4,5,6,8,9,10,2),

(2,3,4,5,6,8,9,11,2),

(2,3,4,5,9,10,2),

(2,3,4,5,9,11,2),

(3,4,5,6,8,9,10,2,12,13,14,15),

(3,4,5,6,8,9,11,2,12,13,14,15),

(3,4,5,9,10,2,12,13,14,15),

(3,4,5,9,11,2,12,13,14,15)

(3,4,5,6,8,9,10,2,12,13,16),

(3,4,5,6,8,9,11,2,12,13,16),

(3,4,5,9,10,2,12,13,16),

(3,4,5,9,11,2,12,13,16),

(5,6,7,5),

(6,7,5,9,10,2,12,13,14,15),

(6,7,5,9,11,2,12,13,14,15),

(6,7,5,9,10,2,12,13,16)

(6,7,5,9,11,2,12,13,16)

(13,14,15,13)

(14,15,13,16)}