图算法

一.无向图

1.邻接表数据结构

1）  图中顶点用一个一维数组存储，当然也可以用单链表来存储，不过用数组可以较容易的读取顶点信息，更加方便。另外，对于顶点数组中，每个数据元素还需要存储指向第一个邻接点的指针，以便于查找该顶点的边信息。

2）  图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点vi的边表，有向图则称为以vi为弧尾的出边表。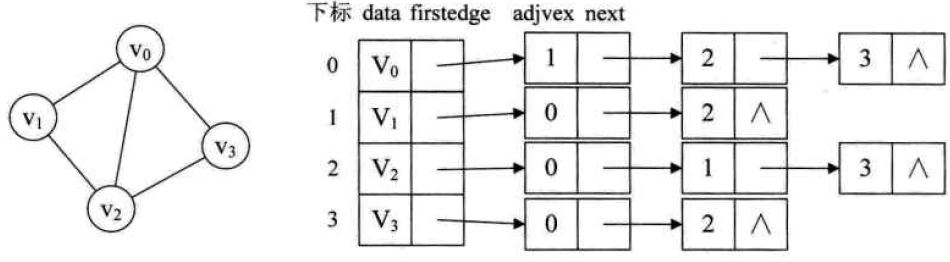

package sort;

import edu.princeton.cs.algs4.Bag;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;
import java.util.NoSuchElementException;
import java.util.Stack;

public class Graph {
    private static final String NEWLINE = System.getProperty("line.separator");

    private final int V;
    private int E;
    private Bag<Integer>[] adj;

    //创建一个含有V个顶点但不含有边的图
    public Graph(int V) {
        if (V < 0) throw new IllegalArgumentException("Number of vertices must be nonnegative");
        this.V = V;
        this.E = 0;
        adj = (Bag<Integer>[]) new Bag[V];
        for (int v = 0; v < V; v++) {
            adj[v] = new Bag<Integer>();
        }
    }

    //从标准输入流in读入一幅图
    public Graph(In in) {
        if (in == null) throw new IllegalArgumentException("argument is null");
        try {
            this.V = in.readInt();
            if (V < 0) throw new IllegalArgumentException("number of vertices in a Graph must be nonnegative");
            adj = (Bag<Integer>[]) new Bag[V];
            for (int v = 0; v < V; v++) {
                adj[v] = new Bag<Integer>();
            }
            int E = in.readInt();
            if (E < 0) throw new IllegalArgumentException("number of edges in a Graph must be nonnegative");
            for (int i = 0; i < E; i++) {
                int v = in.readInt();
                int w = in.readInt();
                validateVertex(v);
                validateVertex(w);
                addEdge(v, w);
            }
        }
        catch (NoSuchElementException e) {
            throw new IllegalArgumentException("invalid input format in Graph constructor", e);
        }
    }

    //深拷贝一幅图
    public Graph(Graph G) {
        this.V = G.V();
        this.E = G.E();
        if (V < 0) throw new IllegalArgumentException("Number of vertices must be nonnegative");

        // update adjacency lists
        adj = (Bag<Integer>[]) new Bag[V];
        for (int v = 0; v < V; v++) {
            adj[v] = new Bag<Integer>();
        }

        for (int v = 0; v < G.V(); v++) {
            // reverse so that adjacency list is in same order as original
            Stack<Integer> reverse = new Stack<Integer>();
            for (int w : G.adj[v]) {
                reverse.push(w);
            }
            for (int w : reverse) {
                adj[v].add(w);
            }
        }
    }

    //返回顶点数
    public int V() {
        return V;
    }

    //返回边数
    public int E() {
        return E;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    //向图中添加一条边v-w
    public void addEdge(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        E++;
        adj[v].add(w);
        adj[w].add(v);
    }

    //和v相邻的所有顶点
    public Iterable<Integer> adj(int v) {
        validateVertex(v);
        return adj[v];
    }

    //返回顶点v的度数
    public int degree(int v) {
        validateVertex(v);
        return adj[v].size();
    }

    public String toString() {
        StringBuilder s = new StringBuilder();
        s.append(V + " vertices, " + E + " edges " + NEWLINE);
        for (int v = 0; v < V; v++) {
            s.append(v + ": ");
            for (int w : adj[v]) {
                s.append(w + " ");
            }
            s.append(NEWLINE);
        }
        return s.toString();
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        Graph G = new Graph(in);
        StdOut.println(G);
    }

}

 2.深度优先搜索

思路：将深度优先搜索比喻成走迷宫。

（1）选择一条没有标记过的通道，在你走过的路上铺上一条绳子。

（2）标记所有你第一次路过的路口和通道。

（3）当你来到一个你标记过的路口时，回退到上一个路口。

（4）当回退的路口已没有可走的通道时继续回退。

 

 

package graph;

import edu.princeton.cs.algs4.Graph;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;

public class DepthFirstSearch {
    private boolean[] marked;    // marked[v] = is there an s-v path?
    private int count;           // number of vertices connected to s

    public DepthFirstSearch(Graph G, int s) {
        marked = new boolean[G.V()];
        validateVertex(s);
        dfs(G, s);
    }

    // 深度优先搜索v顶点
    private void dfs(Graph G, int v) {
        count++;
        marked[v] = true;
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                dfs(G, w);
            }
        }
    }

    //判断v和s是否连通
    public boolean marked(int v) {
        validateVertex(v);
        return marked[v];
    }

    //与s连通的顶点数
    public int count() {
        return count;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        int V = marked.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        Graph G = new Graph(in);
        int s = Integer.parseInt(args[1]);
        DepthFirstSearch search = new DepthFirstSearch(G, s);
        for (int v = 0; v < G.V(); v++) {
            if (search.marked(v))
                StdOut.print(v + " ");
        }

        StdOut.println();
        if (search.count() != G.V()) StdOut.println("NOT connected");
        else                         StdOut.println("connected");
    }

}

 

3.使用深度优先搜索查找图中的路径

package graph;

import edu.princeton.cs.algs4.Graph;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;
import java.util.Stack;

public class DepthFirstPaths {
    private boolean[] marked;    // marked[v] = is there an s-v path?
    private int[] edgeTo;        // edgeTo[v] = last edge on s-v path
    private final int s;         // source vertex

    public DepthFirstPaths(Graph G, int s) {
        this.s = s;
        edgeTo = new int[G.V()];
        marked = new boolean[G.V()];
        validateVertex(s);
        dfs(G, s);
    }

    // 深度优先搜索
    private void dfs(Graph G, int v) {
        marked[v] = true;
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                edgeTo[w] = v;
                dfs(G, w);
            }
        }
    }

    //是否存在从s到v的路径
    public boolean hasPathTo(int v) {
        validateVertex(v);
        return marked[v];
    }

    //s到v的路径，如果不存在则返回null
    public Iterable<Integer> pathTo(int v) {
        validateVertex(v);
        if (!hasPathTo(v)) return null;
        Stack<Integer> path = new Stack<Integer>();
        for (int x = v; x != s; x = edgeTo[x])
            path.push(x);
        path.push(s);
        return path;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        int V = marked.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        Graph G = new Graph(in);
        int s = Integer.parseInt(args[1]);
        DepthFirstPaths dfs = new DepthFirstPaths(G, s);

        for (int v = 0; v < G.V(); v++) {
            if (dfs.hasPathTo(v)) {
                StdOut.printf("%d to %d:  ", s, v);
                for (int x : dfs.pathTo(v)) {
                    if (x == s) StdOut.print(x);
                    else        StdOut.print("-" + x);
                }
                StdOut.println();
            }

            else {
                StdOut.printf("%d to %d:  not connected\n", s, v);
            }

        }
    }

}

4.广度优先搜索（最短路径）

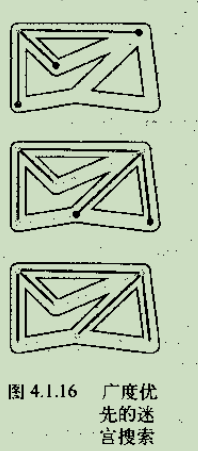
 思路：广度优先搜索就像是一组人在一起朝各个方向走这座迷宫，每个人都有自己的绳子。当出现叉路时，可以假设一个探险者可以分裂为更多的人来搜索它们，当两个探险者相遇时，会合二为一。

 

 

package graph;

import edu.princeton.cs.algs4.Graph;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.Queue;
import edu.princeton.cs.algs4.StdOut;
import java.util.Stack;

public class BreadthFirstPaths {
    private static final int INFINITY = Integer.MAX_VALUE;
    private boolean[] marked;  // marked[v] = is there an s-v path
    private int[] edgeTo;      // edgeTo[v] = previous edge on shortest s-v path
    private int[] distTo;      // distTo[v] = number of edges shortest s-v path

    public BreadthFirstPaths(Graph G, int s) {
        marked = new boolean[G.V()];
        distTo = new int[G.V()];
        edgeTo = new int[G.V()];
        validateVertex(s);
        bfs(G, s);

        assert check(G, s);
    }

    public BreadthFirstPaths(Graph G, Iterable<Integer> sources) {
        marked = new boolean[G.V()];
        distTo = new int[G.V()];
        edgeTo = new int[G.V()];
        for (int v = 0; v < G.V(); v++)
            distTo[v] = INFINITY;
        validateVertices(sources);
        bfs(G, sources);
    }


    // 广度优先搜索
    private void bfs(Graph G, int s) {
        Queue<Integer> q = new Queue<Integer>();
        for (int v = 0; v < G.V(); v++)
            distTo[v] = INFINITY;
        distTo[s] = 0;
        marked[s] = true;
        q.enqueue(s);

        while (!q.isEmpty()) {
            int v = q.dequeue();
            for (int w : G.adj(v)) {
                if (!marked[w]) {
                    edgeTo[w] = v;
                    distTo[w] = distTo[v] + 1;
                    marked[w] = true;
                    q.enqueue(w);
                }
            }
        }
    }

    // breadth-first search from multiple sources
    private void bfs(Graph G, Iterable<Integer> sources) {
        Queue<Integer> q = new Queue<Integer>();
        for (int s : sources) {
            marked[s] = true;
            distTo[s] = 0;
            q.enqueue(s);
        }
        while (!q.isEmpty()) {
            int v = q.dequeue();
            for (int w : G.adj(v)) {
                if (!marked[w]) {
                    edgeTo[w] = v;
                    distTo[w] = distTo[v] + 1;
                    marked[w] = true;
                    q.enqueue(w);
                }
            }
        }
    }

    //判断v是否可达
    public boolean hasPathTo(int v) {
        validateVertex(v);
        return marked[v];
    }

    //返回顶点到v的边数
    public int distTo(int v) {
        validateVertex(v);
        return distTo[v];
    }

    //顶点到v的最短路径
    public Iterable<Integer> pathTo(int v) {
        validateVertex(v);
        if (!hasPathTo(v)) return null;
        Stack<Integer> path = new Stack<Integer>();
        int x;
        for (x = v; distTo[x] != 0; x = edgeTo[x])
            path.push(x);
        path.push(x);
        return path;
    }


    // check optimality conditions for single source
    private boolean check(Graph G, int s) {

        // check that the distance of s = 0
        if (distTo[s] != 0) {
            StdOut.println("distance of source " + s + " to itself = " + distTo[s]);
            return false;
        }

        // check that for each edge v-w dist[w] <= dist[v] + 1
        // provided v is reachable from s
        for (int v = 0; v < G.V(); v++) {
            for (int w : G.adj(v)) {
                if (hasPathTo(v) != hasPathTo(w)) {
                    StdOut.println("edge " + v + "-" + w);
                    StdOut.println("hasPathTo(" + v + ") = " + hasPathTo(v));
                    StdOut.println("hasPathTo(" + w + ") = " + hasPathTo(w));
                    return false;
                }
                if (hasPathTo(v) && (distTo[w] > distTo[v] + 1)) {
                    StdOut.println("edge " + v + "-" + w);
                    StdOut.println("distTo[" + v + "] = " + distTo[v]);
                    StdOut.println("distTo[" + w + "] = " + distTo[w]);
                    return false;
                }
            }
        }

        // check that v = edgeTo[w] satisfies distTo[w] = distTo[v] + 1
        // provided v is reachable from s
        for (int w = 0; w < G.V(); w++) {
            if (!hasPathTo(w) || w == s) continue;
            int v = edgeTo[w];
            if (distTo[w] != distTo[v] + 1) {
                StdOut.println("shortest path edge " + v + "-" + w);
                StdOut.println("distTo[" + v + "] = " + distTo[v]);
                StdOut.println("distTo[" + w + "] = " + distTo[w]);
                return false;
            }
        }

        return true;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        int V = marked.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertices(Iterable<Integer> vertices) {
        if (vertices == null) {
            throw new IllegalArgumentException("argument is null");
        }
        int V = marked.length;
        for (int v : vertices) {
            if (v < 0 || v >= V) {
                throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
            }
        }
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        Graph G = new Graph(in);
        // StdOut.println(G);
        int s = Integer.parseInt(args[1]);
        BreadthFirstPaths bfs = new BreadthFirstPaths(G, s);

        for (int v = 0; v < G.V(); v++) {
            if (bfs.hasPathTo(v)) {
                StdOut.printf("%d to %d (%d):  ", s, v, bfs.distTo(v));
                for (int x : bfs.pathTo(v)) {
                    if (x == s) StdOut.print(x);
                    else        StdOut.print("-" + x);
                }
                StdOut.println();
            }
            else {
                StdOut.printf("%d to %d (-):  not connected\n", s, v);
            }

        }
    }
}

5.使用深度优先搜索找出图中的所有连通分量

package graph;

import edu.princeton.cs.algs4.*;

public class CC {
    private boolean[] marked;   // marked[v] = has vertex v been marked?
    private int[] id;           // id[v] = id of connected component containing v
    private int[] size;         // size[id] = number of vertices in given component
    private int count;          // number of connected components

    public CC(Graph G) {
        marked = new boolean[G.V()];
        id = new int[G.V()];
        size = new int[G.V()];
        for (int v = 0; v < G.V(); v++) {
            if (!marked[v]) {
                dfs(G, v);
                count++;
            }
        }
    }

    public CC(EdgeWeightedGraph G) {
        marked = new boolean[G.V()];
        id = new int[G.V()];
        size = new int[G.V()];
        for (int v = 0; v < G.V(); v++) {
            if (!marked[v]) {
                dfs(G, v);
                count++;
            }
        }
    }

    // depth-first search for a Graph
    private void dfs(Graph G, int v) {
        marked[v] = true;
        id[v] = count;
        size[count]++;
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                dfs(G, w);
            }
        }
    }

    // depth-first search for an EdgeWeightedGraph
    private void dfs(EdgeWeightedGraph G, int v) {
        marked[v] = true;
        id[v] = count;
        size[count]++;
        for (Edge e : G.adj(v)) {
            int w = e.other(v);
            if (!marked[w]) {
                dfs(G, w);
            }
        }
    }

    //v所在的连通分量的标识符
    public int id(int v) {
        validateVertex(v);
        return id[v];
    }

    public int size(int v) {
        validateVertex(v);
        return size[id[v]];
    }

    //连通分量数
    public int count() {
        return count;
    }

    //v和w连通吗
    public boolean connected(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        return id(v) == id(w);
    }

    @Deprecated
    public boolean areConnected(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        return id(v) == id(w);
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        int V = marked.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        Graph G = new Graph(in);
        CC cc = new CC(G);

        // number of connected components
        int m = cc.count();
        StdOut.println(m + " components");

        // compute list of vertices in each connected component
        Queue<Integer>[] components = (Queue<Integer>[]) new Queue[m];
        for (int i = 0; i < m; i++) {
            components[i] = new Queue<Integer>();
        }
        for (int v = 0; v < G.V(); v++) {
            components[cc.id(v)].enqueue(v);
        }

        // print results
        for (int i = 0; i < m; i++) {
            for (int v : components[i]) {
                StdOut.print(v + " ");
            }
            StdOut.println();
        }
    }
}

6.符号图的数据结构

package graph;

import edu.princeton.cs.algs4.*;

public class SymbolGraph {
    private ST<String, Integer> st;  // string -> index
    private String[] keys;           // index  -> string
    private Graph graph;             // the underlying graph

    public SymbolGraph(String filename, String delimiter) {
        st = new ST<String, Integer>();

        // First pass builds the index by reading strings to associate
        // distinct strings with an index
        In in = new In(filename);
        // while (in.hasNextLine()) {
        while (!in.isEmpty()) {
            String[] a = in.readLine().split(delimiter);
            for (int i = 0; i < a.length; i++) {
                if (!st.contains(a[i]))
                    st.put(a[i], st.size());
            }
        }

        // inverted index to get string keys in an array
        keys = new String[st.size()];
        for (String name : st.keys()) {
            keys[st.get(name)] = name;
        }

        // second pass builds the graph by connecting first vertex on each
        // line to all others
        graph = new Graph(st.size());
        in = new In(filename);
        while (in.hasNextLine()) {
            String[] a = in.readLine().split(delimiter);
            int v = st.get(a[0]);
            for (int i = 1; i < a.length; i++) {
                int w = st.get(a[i]);
                graph.addEdge(v, w);
            }
        }
    }

    //s是一个顶点吗
    public boolean contains(String s) {
        return st.contains(s);
    }

    @Deprecated
    public int index(String s) {
        return st.get(s);
    }


    //s的索引
    public int indexOf(String s) {
        return st.get(s);
    }

    @Deprecated
    public String name(int v) {
        validateVertex(v);
        return keys[v];
    }

    //索引v的顶点名
    public String nameOf(int v) {
        validateVertex(v);
        return keys[v];
    }

    @Deprecated
    public Graph G() {
        return graph;
    }

    public Graph graph() {
        return graph;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        int V = graph.V();
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    public static void main(String[] args) {
        String filename  = args[0];
        String delimiter = args[1];
        SymbolGraph sg = new SymbolGraph(filename, delimiter);
        Graph graph = sg.graph();
        while (StdIn.hasNextLine()) {
            String source = StdIn.readLine();
            if (sg.contains(source)) {
                int s = sg.index(source);
                for (int v : graph.adj(s)) {
                    StdOut.println("   " + sg.name(v));
                }
            }
            else {
                StdOut.println("input not contain '" + source + "'");
            }
        }
    }
}

 

二.有向图

 1.有向图数据结构

package graph;

import edu.princeton.cs.algs4.Bag;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.Stack;
import edu.princeton.cs.algs4.StdOut;
import java.util.NoSuchElementException;

public class Digraph {
    private static final String NEWLINE = System.getProperty("line.separator");

    private final int V;           // number of vertices in this digraph
    private int E;                 // number of edges in this digraph
    private Bag<Integer>[] adj;    // adj[v] = adjacency list for vertex v
    private int[] indegree;        // indegree[v] = indegree of vertex v

    public Digraph(int V) {
        if (V < 0) throw new IllegalArgumentException("Number of vertices in a Digraph must be nonnegative");
        this.V = V;
        this.E = 0;
        indegree = new int[V];
        adj = (Bag<Integer>[]) new Bag[V];
        for (int v = 0; v < V; v++) {
            adj[v] = new Bag<Integer>();
        }
    }

    public Digraph(In in) {
        if (in == null) throw new IllegalArgumentException("argument is null");
        try {
            this.V = in.readInt();
            if (V < 0) throw new IllegalArgumentException("number of vertices in a Digraph must be nonnegative");
            indegree = new int[V];
            adj = (Bag<Integer>[]) new Bag[V];
            for (int v = 0; v < V; v++) {
                adj[v] = new Bag<Integer>();
            }
            int E = in.readInt();
            if (E < 0) throw new IllegalArgumentException("number of edges in a Digraph must be nonnegative");
            for (int i = 0; i < E; i++) {
                int v = in.readInt();
                int w = in.readInt();
                addEdge(v, w);
            }
        }
        catch (NoSuchElementException e) {
            throw new IllegalArgumentException("invalid input format in Digraph constructor", e);
        }
    }

    public Digraph(Digraph G) {
        if (G == null) throw new IllegalArgumentException("argument is null");

        this.V = G.V();
        this.E = G.E();
        if (V < 0) throw new IllegalArgumentException("Number of vertices in a Digraph must be nonnegative");

        // update indegrees
        indegree = new int[V];
        for (int v = 0; v < V; v++)
            this.indegree[v] = G.indegree(v);

        // update adjacency lists
        adj = (Bag<Integer>[]) new Bag[V];
        for (int v = 0; v < V; v++) {
            adj[v] = new Bag<Integer>();
        }

        for (int v = 0; v < G.V(); v++) {
            // reverse so that adjacency list is in same order as original
            Stack<Integer> reverse = new Stack<Integer>();
            for (int w : G.adj[v]) {
                reverse.push(w);
            }
            for (int w : reverse) {
                adj[v].add(w);
            }
        }
    }

    //顶点总数
    public int V() {
        return V;
    }

    //边的总数
    public int E() {
        return E;
    }


    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    //向有向图中添加一条边v->w
    public void addEdge(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        adj[v].add(w);
        indegree[w]++;
        E++;
    }

    //由v指出的边所连接的所有顶点
    public Iterable<Integer> adj(int v) {
        validateVertex(v);
        return adj[v];
    }

    public int outdegree(int v) {
        validateVertex(v);
        return adj[v].size();
    }

    //到顶点v的有向边数
    public int indegree(int v) {
        validateVertex(v);
        return indegree[v];
    }

    //该图的反向图
    public Digraph reverse() {
        Digraph reverse = new Digraph(V);
        for (int v = 0; v < V; v++) {
            for (int w : adj(v)) {
                reverse.addEdge(w, v);
            }
        }
        return reverse;
    }

    public String toString() {
        StringBuilder s = new StringBuilder();
        s.append(V + " vertices, " + E + " edges " + NEWLINE);
        for (int v = 0; v < V; v++) {
            s.append(String.format("%d: ", v));
            for (int w : adj[v]) {
                s.append(String.format("%d ", w));
            }
            s.append(NEWLINE);
        }
        return s.toString();
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        Digraph G = new Digraph(in);
        StdOut.println(G);
    }

}

2.有向图中的可达性

package graph;

import edu.princeton.cs.algs4.Bag;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;

public class DirectedDFS {
    private boolean[] marked;  // marked[v] = true iff v is reachable from source(s)
    private int count;         // number of vertices reachable from source(s)

    public DirectedDFS(Digraph G, int s) {
        marked = new boolean[G.V()];
        validateVertex(s);
        dfs(G, s);
    }

    public DirectedDFS(Digraph G, Iterable<Integer> sources) {
        marked = new boolean[G.V()];
        validateVertices(sources);
        for (int v : sources) {
            if (!marked[v]) dfs(G, v);
        }
    }

    private void dfs(Digraph G, int v) {
        count++;
        marked[v] = true;
        for (int w : G.adj(v)) {
            if (!marked[w]) dfs(G, w);
        }
    }

    public boolean marked(int v) {
        validateVertex(v);
        return marked[v];
    }

    public int count() {
        return count;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        int V = marked.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertices(Iterable<Integer> vertices) {
        if (vertices == null) {
            throw new IllegalArgumentException("argument is null");
        }
        int V = marked.length;
        for (int v : vertices) {
            if (v < 0 || v >= V) {
                throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
            }
        }
    }

    public static void main(String[] args) {

        // read in digraph from command-line argument
        In in = new In(args[0]);
        Digraph G = new Digraph(in);

        // read in sources from command-line arguments
        Bag<Integer> sources = new Bag<Integer>();
        for (int i = 1; i < args.length; i++) {
            int s = Integer.parseInt(args[i]);
            sources.add(s);
        }

        // multiple-source reachability
        DirectedDFS dfs = new DirectedDFS(G, sources);

        // print out vertices reachable from sources
        for (int v = 0; v < G.V(); v++) {
            if (dfs.marked(v)) StdOut.print(v + " ");
        }
        StdOut.println();
    }

}

3.寻找有向环

package graph;

import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.Stack;
import edu.princeton.cs.algs4.StdOut;

public class DirectedCycle {
    private boolean[] marked;        // marked[v] = has vertex v been marked?
    private int[] edgeTo;            // edgeTo[v] = previous vertex on path to v
    private boolean[] onStack;       // onStack[v] = is vertex on the stack?
    private Stack<Integer> cycle;    // directed cycle (or null if no such cycle)

    public DirectedCycle(Digraph G) {
        marked  = new boolean[G.V()];
        onStack = new boolean[G.V()];
        edgeTo  = new int[G.V()];
        for (int v = 0; v < G.V(); v++)
            if (!marked[v] && cycle == null) dfs(G, v);
    }

    // check that algorithm computes either the topological order or finds a directed cycle
    private void dfs(Digraph G, int v) {
        onStack[v] = true;
        marked[v] = true;
        for (int w : G.adj(v)) {

            // short circuit if directed cycle found
            if (cycle != null) return;

                // found new vertex, so recur
            else if (!marked[w]) {
                edgeTo[w] = v;
                dfs(G, w);
            }

            // trace back directed cycle
            else if (onStack[w]) {
                cycle = new Stack<Integer>();
                for (int x = v; x != w; x = edgeTo[x]) {
                    cycle.push(x);
                }
                cycle.push(w);
                cycle.push(v);
                assert check();
            }
        }
        onStack[v] = false;
    }

    //是否含有有向环
    public boolean hasCycle() {
        return cycle != null;
    }

    //有向环中的所有顶点
    public Iterable<Integer> cycle() {
        return cycle;
    }


    // certify that digraph has a directed cycle if it reports one
    private boolean check() {

        if (hasCycle()) {
            // verify cycle
            int first = -1, last = -1;
            for (int v : cycle()) {
                if (first == -1) first = v;
                last = v;
            }
            if (first != last) {
                System.err.printf("cycle begins with %d and ends with %d\n", first, last);
                return false;
            }
        }


        return true;
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        Digraph G = new Digraph(in);

        DirectedCycle finder = new DirectedCycle(G);
        if (finder.hasCycle()) {
            StdOut.print("Directed cycle: ");
            for (int v : finder.cycle()) {
                StdOut.print(v + " ");
            }
            StdOut.println();
        }

        else {
            StdOut.println("No directed cycle");
        }
        StdOut.println();
    }

}

4.有向图中基于深度优先搜索的顶点排序

package graph;

import edu.princeton.cs.algs4.*;

public class DepthFirstOrder {
    private boolean[] marked;          // marked[v] = has v been marked in dfs?
    private int[] pre;                 // pre[v]    = preorder  number of v
    private int[] post;                // post[v]   = postorder number of v
    private Queue<Integer> preorder;   // vertices in preorder
    private Queue<Integer> postorder;  // vertices in postorder
    private int preCounter;            // counter or preorder numbering
    private int postCounter;           // counter for postorder numbering

    public DepthFirstOrder(Digraph G) {
        pre    = new int[G.V()];
        post   = new int[G.V()];
        postorder = new Queue<Integer>();
        preorder  = new Queue<Integer>();
        marked    = new boolean[G.V()];
        for (int v = 0; v < G.V(); v++)
            if (!marked[v]) dfs(G, v);

        assert check();
    }

    public DepthFirstOrder(EdgeWeightedDigraph G) {
        pre    = new int[G.V()];
        post   = new int[G.V()];
        postorder = new Queue<Integer>();
        preorder  = new Queue<Integer>();
        marked    = new boolean[G.V()];
        for (int v = 0; v < G.V(); v++)
            if (!marked[v]) dfs(G, v);
    }

    // run DFS in digraph G from vertex v and compute preorder/postorder
    private void dfs(Digraph G, int v) {
        marked[v] = true;
        pre[v] = preCounter++;
        preorder.enqueue(v);
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                dfs(G, w);
            }
        }
        postorder.enqueue(v);
        post[v] = postCounter++;
    }

    // run DFS in edge-weighted digraph G from vertex v and compute preorder/postorder
    private void dfs(EdgeWeightedDigraph G, int v) {
        marked[v] = true;
        pre[v] = preCounter++;
        preorder.enqueue(v);
        for (DirectedEdge e : G.adj(v)) {
            int w = e.to();
            if (!marked[w]) {
                dfs(G, w);
            }
        }
        postorder.enqueue(v);
        post[v] = postCounter++;
    }

    public int pre(int v) {
        validateVertex(v);
        return pre[v];
    }

    public int post(int v) {
        validateVertex(v);
        return post[v];
    }

    //所有顶点的后序排序
    public Iterable<Integer> post() {
        return postorder;
    }

    //所有顶点的前序排序
    public Iterable<Integer> pre() {
        return preorder;
    }

    //所有顶点的逆后序排序
    public Iterable<Integer> reversePost() {
        Stack<Integer> reverse = new Stack<Integer>();
        for (int v : postorder)
            reverse.push(v);
        return reverse;
    }


    // check that pre() and post() are consistent with pre(v) and post(v)
    private boolean check() {

        // check that post(v) is consistent with post()
        int r = 0;
        for (int v : post()) {
            if (post(v) != r) {
                StdOut.println("post(v) and post() inconsistent");
                return false;
            }
            r++;
        }

        // check that pre(v) is consistent with pre()
        r = 0;
        for (int v : pre()) {
            if (pre(v) != r) {
                StdOut.println("pre(v) and pre() inconsistent");
                return false;
            }
            r++;
        }

        return true;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        int V = marked.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        Digraph G = new Digraph(in);

        DepthFirstOrder dfs = new DepthFirstOrder(G);
        StdOut.println("   v  pre post");
        StdOut.println("--------------");
        for (int v = 0; v < G.V(); v++) {
            StdOut.printf("%4d %4d %4d\n", v, dfs.pre(v), dfs.post(v));
        }

        StdOut.print("Preorder:  ");
        for (int v : dfs.pre()) {
            StdOut.print(v + " ");
        }
        StdOut.println();

        StdOut.print("Postorder: ");
        for (int v : dfs.post()) {
            StdOut.print(v + " ");
        }
        StdOut.println();

        StdOut.print("Reverse postorder: ");
        for (int v : dfs.reversePost()) {
            StdOut.print(v + " ");
        }
        StdOut.println();
    }
}

5.拓扑排序

package graph;

import edu.princeton.cs.algs4.EdgeWeightedDigraph;
import edu.princeton.cs.algs4.EdgeWeightedDirectedCycle;
import edu.princeton.cs.algs4.StdOut;
import edu.princeton.cs.algs4.SymbolDigraph;

public class Topological {
    private Iterable<Integer> order;  // topological order
    private int[] rank;               // rank[v] = rank of vertex v in order

    public Topological(Digraph G) {
        DirectedCycle finder = new DirectedCycle(G);
        if (!finder.hasCycle()) {
            DepthFirstOrder dfs = new DepthFirstOrder(G);
            order = dfs.reversePost();
            rank = new int[G.V()];
            int i = 0;
            for (int v : order)
                rank[v] = i++;
        }
    }

    public Topological(EdgeWeightedDigraph G) {
        EdgeWeightedDirectedCycle finder = new EdgeWeightedDirectedCycle(G);
        if (!finder.hasCycle()) {
            DepthFirstOrder dfs = new DepthFirstOrder(G);
            order = dfs.reversePost();
        }
    }

    //拓扑有序的所有顶点
    public Iterable<Integer> order() {
        return order;
    }

    public boolean hasOrder() {
        return order != null;
    }

    @Deprecated
    public boolean isDAG() {
        return hasOrder();
    }

    public int rank(int v) {
        validateVertex(v);
        if (hasOrder()) return rank[v];
        else            return -1;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        int V = rank.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    public static void main(String[] args) {
        String filename  = args[0];
        String delimiter = args[1];
        SymbolDigraph sg = new SymbolDigraph(filename, delimiter);
        Topological topological = new Topological(sg.digraph());
        for (int v : topological.order()) {
            StdOut.println(sg.nameOf(v));
        }
    }
}

 

三.加权无向图

 1.加权边数据结构

package graph;

import edu.princeton.cs.algs4.StdOut;

public class Edge implements Comparable<Edge> {

    private final int v;
    private final int w;
    private final double weight;

    public Edge(int v, int w, double weight) {
        if (v < 0) throw new IllegalArgumentException("vertex index must be a nonnegative integer");
        if (w < 0) throw new IllegalArgumentException("vertex index must be a nonnegative integer");
        if (Double.isNaN(weight)) throw new IllegalArgumentException("Weight is NaN");
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    //边的权重
    public double weight() {
        return weight;
    }

    //边两边的顶点之一
    public int either() {
        return v;
    }

    //另一个顶点
    public int other(int vertex) {
        if      (vertex == v) return w;
        else if (vertex == w) return v;
        else throw new IllegalArgumentException("Illegal endpoint");
    }

    @Override
    public int compareTo(Edge that) {
        return Double.compare(this.weight, that.weight);
    }

    public String toString() {
        return String.format("%d-%d %.5f", v, w, weight);
    }

    public static void main(String[] args) {
        Edge e = new Edge(12, 34, 5.67);
        StdOut.println(e);
    }
}

2.加权无向图数据结构

package graph;

import edu.princeton.cs.algs4.*;
import java.util.NoSuchElementException;

public class EdgeWeightedGraph {
    private static final String NEWLINE = System.getProperty("line.separator");

    private final int V;
    private int E;
    private Bag<Edge>[] adj;

    public EdgeWeightedGraph(int V) {
        if (V < 0) throw new IllegalArgumentException("Number of vertices must be nonnegative");
        this.V = V;
        this.E = 0;
        adj = (Bag<Edge>[]) new Bag[V];
        for (int v = 0; v < V; v++) {
            adj[v] = new Bag<Edge>();
        }
    }

    public EdgeWeightedGraph(int V, int E) {
        this(V);
        if (E < 0) throw new IllegalArgumentException("Number of edges must be nonnegative");
        for (int i = 0; i < E; i++) {
            int v = StdRandom.uniform(V);
            int w = StdRandom.uniform(V);
            double weight = Math.round(100 * StdRandom.uniform()) / 100.0;
            Edge e = new Edge(v, w, weight);
            addEdge(e);
        }
    }

    public EdgeWeightedGraph(In in) {
        if (in == null) throw new IllegalArgumentException("argument is null");

        try {
            V = in.readInt();
            adj = (Bag<Edge>[]) new Bag[V];
            for (int v = 0; v < V; v++) {
                adj[v] = new Bag<Edge>();
            }

            int E = in.readInt();
            if (E < 0) throw new IllegalArgumentException("Number of edges must be nonnegative");
            for (int i = 0; i < E; i++) {
                int v = in.readInt();
                int w = in.readInt();
                validateVertex(v);
                validateVertex(w);
                double weight = in.readDouble();
                Edge e = new Edge(v, w, weight);
                addEdge(e);
            }
        }
        catch (NoSuchElementException e) {
            throw new IllegalArgumentException("invalid input format in EdgeWeightedGraph constructor", e);
        }

    }

    public EdgeWeightedGraph(EdgeWeightedGraph G) {
        this(G.V());
        this.E = G.E();
        for (int v = 0; v < G.V(); v++) {
            // reverse so that adjacency list is in same order as original
            Stack<Edge> reverse = new Stack<Edge>();
            for (Edge e : G.adj[v]) {
                reverse.push(e);
            }
            for (Edge e : reverse) {
                adj[v].add(e);
            }
        }
    }

    //图的顶点数
    public int V() {
        return V;
    }

    //图的边数
    public int E() {
        return E;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    //向图中添加一条边
    public void addEdge(Edge e) {
        int v = e.either();
        int w = e.other(v);
        validateVertex(v);
        validateVertex(w);
        adj[v].add(e);
        adj[w].add(e);
        E++;
    }

    //和v相关联的所有边
    public Iterable<Edge> adj(int v) {
        validateVertex(v);
        return adj[v];
    }

    public int degree(int v) {
        validateVertex(v);
        return adj[v].size();
    }

    //图的所有边
    public Iterable<Edge> edges() {
        Bag<Edge> list = new Bag<Edge>();
        for (int v = 0; v < V; v++) {
            int selfLoops = 0;
            for (Edge e : adj(v)) {
                if (e.other(v) > v) {
                    list.add(e);
                }
                // add only one copy of each self loop (self loops will be consecutive)
                else if (e.other(v) == v) {
                    if (selfLoops % 2 == 0) list.add(e);
                    selfLoops++;
                }
            }
        }
        return list;
    }

    public String toString() {
        StringBuilder s = new StringBuilder();
        s.append(V + " " + E + NEWLINE);
        for (int v = 0; v < V; v++) {
            s.append(v + ": ");
            for (Edge e : adj[v]) {
                s.append(e + "  ");
            }
            s.append(NEWLINE);
        }
        return s.toString();
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        EdgeWeightedGraph G = new EdgeWeightedGraph(in);
        StdOut.println(G);
    }

}

3.最小生成树的Prim算法的延时实现

package graph;

import edu.princeton.cs.algs4.*;

public class LazyPrimMST {
    private static final double FLOATING_POINT_EPSILON = 1E-12;

    private double weight;       // total weight of MST
    private Queue<Edge> mst;     // edges in the MST
    private boolean[] marked;    // marked[v] = true iff v on tree
    private MinPQ<Edge> pq;      // edges with one endpoint in tree

    public LazyPrimMST(EdgeWeightedGraph G) {
        mst = new Queue<Edge>();
        pq = new MinPQ<Edge>();
        marked = new boolean[G.V()];
        for (int v = 0; v < G.V(); v++)     // run Prim from all vertices to
            if (!marked[v]) prim(G, v);     // get a minimum spanning forest

        // check optimality conditions
        assert check(G);
    }

    // run Prim's algorithm
    private void prim(EdgeWeightedGraph G, int s) {
        scan(G, s);
        while (!pq.isEmpty()) {                        // better to stop when mst has V-1 edges
            Edge e = pq.delMin();                      // smallest edge on pq
            int v = e.either(), w = e.other(v);        // two endpoints
            assert marked[v] || marked[w];
            if (marked[v] && marked[w]) continue;      // lazy, both v and w already scanned
            mst.enqueue(e);                            // add e to MST
            weight += e.weight();
            if (!marked[v]) scan(G, v);               // v becomes part of tree
            if (!marked[w]) scan(G, w);               // w becomes part of tree
        }
    }

    // add all edges e incident to v onto pq if the other endpoint has not yet been scanned
    private void scan(EdgeWeightedGraph G, int v) {
        assert !marked[v];
        marked[v] = true;
        for (Edge e : G.adj(v))
            if (!marked[e.other(v)]) pq.insert(e);
    }

    public Iterable<Edge> edges() {
        return mst;
    }

    public double weight() {
        return weight;
    }

    // check optimality conditions (takes time proportional to E V lg* V)
    private boolean check(EdgeWeightedGraph G) {

        // check weight
        double totalWeight = 0.0;
        for (Edge e : edges()) {
            totalWeight += e.weight();
        }
        if (Math.abs(totalWeight - weight()) > FLOATING_POINT_EPSILON) {
            System.err.printf("Weight of edges does not equal weight(): %f vs. %f\n", totalWeight, weight());
            return false;
        }

        // check that it is acyclic
        UF uf = new UF(G.V());
        for (Edge e : edges()) {
            int v = e.either(), w = e.other(v);
            if (uf.find(v) == uf.find(w)) {
                System.err.println("Not a forest");
                return false;
            }
            uf.union(v, w);
        }

        // check that it is a spanning forest
        for (Edge e : G.edges()) {
            int v = e.either(), w = e.other(v);
            if (uf.find(v) != uf.find(w)) {
                System.err.println("Not a spanning forest");
                return false;
            }
        }

        // check that it is a minimal spanning forest (cut optimality conditions)
        for (Edge e : edges()) {

            // all edges in MST except e
            uf = new UF(G.V());
            for (Edge f : mst) {
                int x = f.either(), y = f.other(x);
                if (f != e) uf.union(x, y);
            }

            // check that e is min weight edge in crossing cut
            for (Edge f : G.edges()) {
                int x = f.either(), y = f.other(x);
                if (uf.find(x) != uf.find(y)) {
                    if (f.weight() < e.weight()) {
                        System.err.println("Edge " + f + " violates cut optimality conditions");
                        return false;
                    }
                }
            }

        }

        return true;
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        EdgeWeightedGraph G = new EdgeWeightedGraph(in);
        LazyPrimMST mst = new LazyPrimMST(G);
        for (Edge e : mst.edges()) {
            StdOut.println(e);
        }
        StdOut.printf("%.5f\n", mst.weight());
    }
}

4.最小生成树的Prim算法（即时版本）

package graph;

import edu.princeton.cs.algs4.*;

public class PrimMST {
    private static final double FLOATING_POINT_EPSILON = 1E-12;

    private Edge[] edgeTo;        // edgeTo[v] = shortest edge from tree vertex to non-tree vertex
    private double[] distTo;      // distTo[v] = weight of shortest such edge
    private boolean[] marked;     // marked[v] = true if v on tree, false otherwise
    private IndexMinPQ<Double> pq;

    public PrimMST(EdgeWeightedGraph G) {
        edgeTo = new Edge[G.V()];
        distTo = new double[G.V()];
        marked = new boolean[G.V()];
        pq = new IndexMinPQ<Double>(G.V());
        for (int v = 0; v < G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;

        for (int v = 0; v < G.V(); v++)      // run from each vertex to find
            if (!marked[v]) prim(G, v);      // minimum spanning forest

        // check optimality conditions
        assert check(G);
    }

    // run Prim's algorithm in graph G, starting from vertex s
    private void prim(EdgeWeightedGraph G, int s) {
        distTo[s] = 0.0;
        pq.insert(s, distTo[s]);
        while (!pq.isEmpty()) {
            int v = pq.delMin();
            scan(G, v);
        }
    }

    // scan vertex v
    private void scan(EdgeWeightedGraph G, int v) {
        marked[v] = true;
        for (Edge e : G.adj(v)) {
            int w = e.other(v);
            if (marked[w]) continue;         // v-w is obsolete edge
            if (e.weight() < distTo[w]) {
                distTo[w] = e.weight();
                edgeTo[w] = e;
                if (pq.contains(w)) pq.decreaseKey(w, distTo[w]);
                else                pq.insert(w, distTo[w]);
            }
        }
    }

    public Iterable<Edge> edges() {
        Queue<Edge> mst = new Queue<Edge>();
        for (int v = 0; v < edgeTo.length; v++) {
            Edge e = edgeTo[v];
            if (e != null) {
                mst.enqueue(e);
            }
        }
        return mst;
    }

    public double weight() {
        double weight = 0.0;
        for (Edge e : edges())
            weight += e.weight();
        return weight;
    }

    // check optimality conditions (takes time proportional to E V lg* V)
    private boolean check(EdgeWeightedGraph G) {
        // check weight
        double totalWeight = 0.0;
        for (Edge e : edges()) {
            totalWeight += e.weight();
        }
        if (Math.abs(totalWeight - weight()) > FLOATING_POINT_EPSILON) {
            System.err.printf("Weight of edges does not equal weight(): %f vs. %f\n", totalWeight, weight());
            return false;
        }

        // check that it is acyclic
        UF uf = new UF(G.V());
        for (Edge e : edges()) {
            int v = e.either(), w = e.other(v);
            if (uf.find(v) == uf.find(w)) {
                System.err.println("Not a forest");
                return false;
            }
            uf.union(v, w);
        }

        // check that it is a spanning forest
        for (Edge e : G.edges()) {
            int v = e.either(), w = e.other(v);
            if (uf.find(v) != uf.find(w)) {
                System.err.println("Not a spanning forest");
                return false;
            }
        }

        // check that it is a minimal spanning forest (cut optimality conditions)
        for (Edge e : edges()) {

            // all edges in MST except e
            uf = new UF(G.V());
            for (Edge f : edges()) {
                int x = f.either(), y = f.other(x);
                if (f != e) uf.union(x, y);
            }

            // check that e is min weight edge in crossing cut
            for (Edge f : G.edges()) {
                int x = f.either(), y = f.other(x);
                if (uf.find(x) != uf.find(y)) {
                    if (f.weight() < e.weight()) {
                        System.err.println("Edge " + f + " violates cut optimality conditions");
                        return false;
                    }
                }
            }

        }
        return true;
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        EdgeWeightedGraph G = new EdgeWeightedGraph(in);
        PrimMST mst = new PrimMST(G);
        for (Edge e : mst.edges()) {
            StdOut.println(e);
        }
        StdOut.printf("%.5f\n", mst.weight());
    }


}

 5.最小生成树的Kruskal算法

package graph;

import edu.princeton.cs.algs4.*;

public class KruskalMST {
    private static final double FLOATING_POINT_EPSILON = 1E-12;

    private double weight;                        // weight of MST
    private Queue<Edge> mst = new Queue<Edge>();  // edges in MST

    public KruskalMST(EdgeWeightedGraph G) {
        // more efficient to build heap by passing array of edges
        MinPQ<Edge> pq = new MinPQ<Edge>();
        for (Edge e : G.edges()) {
            pq.insert(e);
        }

        // run greedy algorithm
        UF uf = new UF(G.V());
        while (!pq.isEmpty() && mst.size() < G.V() - 1) {
            Edge e = pq.delMin();
            int v = e.either();
            int w = e.other(v);
            if (uf.find(v) != uf.find(w)) { // v-w does not create a cycle
                uf.union(v, w);  // merge v and w components
                mst.enqueue(e);  // add edge e to mst
                weight += e.weight();
            }
        }

        // check optimality conditions
        assert check(G);
    }

    public Iterable<Edge> edges() {
        return mst;
    }

    public double weight() {
        return weight;
    }

    // check optimality conditions (takes time proportional to E V lg* V)
    private boolean check(EdgeWeightedGraph G) {

        // check total weight
        double total = 0.0;
        for (Edge e : edges()) {
            total += e.weight();
        }
        if (Math.abs(total - weight()) > FLOATING_POINT_EPSILON) {
            System.err.printf("Weight of edges does not equal weight(): %f vs. %f\n", total, weight());
            return false;
        }

        // check that it is acyclic
        UF uf = new UF(G.V());
        for (Edge e : edges()) {
            int v = e.either(), w = e.other(v);
            if (uf.find(v) == uf.find(w)) {
                System.err.println("Not a forest");
                return false;
            }
            uf.union(v, w);
        }

        // check that it is a spanning forest
        for (Edge e : G.edges()) {
            int v = e.either(), w = e.other(v);
            if (uf.find(v) != uf.find(w)) {
                System.err.println("Not a spanning forest");
                return false;
            }
        }

        // check that it is a minimal spanning forest (cut optimality conditions)
        for (Edge e : edges()) {

            // all edges in MST except e
            uf = new UF(G.V());
            for (Edge f : mst) {
                int x = f.either(), y = f.other(x);
                if (f != e) uf.union(x, y);
            }

            // check that e is min weight edge in crossing cut
            for (Edge f : G.edges()) {
                int x = f.either(), y = f.other(x);
                if (uf.find(x) != uf.find(y)) {
                    if (f.weight() < e.weight()) {
                        System.err.println("Edge " + f + " violates cut optimality conditions");
                        return false;
                    }
                }
            }

        }

        return true;
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        EdgeWeightedGraph G = new EdgeWeightedGraph(in);
        KruskalMST mst = new KruskalMST(G);
        for (Edge e : mst.edges()) {
            StdOut.println(e);
        }
        StdOut.printf("%.5f\n", mst.weight());
    }
}

 

四.加权有向图

 1.加权有向边的数据结构

package graph;
import edu.princeton.cs.algs4.StdOut;

public class DirectedEdge {
    private final int v;
    private final int w;
    private final double weight;

    public DirectedEdge(int v, int w, double weight) {
        if (v < 0) throw new IllegalArgumentException("Vertex names must be nonnegative integers");
        if (w < 0) throw new IllegalArgumentException("Vertex names must be nonnegative integers");
        if (Double.isNaN(weight)) throw new IllegalArgumentException("Weight is NaN");
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    public int from() {
        return v;
    }

    public int to() {
        return w;
    }

    public double weight() {
        return weight;
    }

    public String toString() {
        return v + "->" + w + " " + String.format("%5.2f", weight);
    }

    public static void main(String[] args) {
        DirectedEdge e = new DirectedEdge(12, 34, 5.67);
        StdOut.println(e);
    }
}

2.加权有向图的数据结构

package graph;

import edu.princeton.cs.algs4.*;

import java.util.NoSuchElementException;

public class EdgeWeightedDigraph {
    private static final String NEWLINE = System.getProperty("line.separator");

    private final int V;                // number of vertices in this digraph
    private int E;                      // number of edges in this digraph
    private Bag<DirectedEdge>[] adj;    // adj[v] = adjacency list for vertex v
    private int[] indegree;             // indegree[v] = indegree of vertex v

    public EdgeWeightedDigraph(int V) {
        if (V < 0) throw new IllegalArgumentException("Number of vertices in a Digraph must be nonnegative");
        this.V = V;
        this.E = 0;
        this.indegree = new int[V];
        adj = (Bag<DirectedEdge>[]) new Bag[V];
        for (int v = 0; v < V; v++)
            adj[v] = new Bag<DirectedEdge>();
    }

    public EdgeWeightedDigraph(int V, int E) {
        this(V);
        if (E < 0) throw new IllegalArgumentException("Number of edges in a Digraph must be nonnegative");
        for (int i = 0; i < E; i++) {
            int v = StdRandom.uniform(V);
            int w = StdRandom.uniform(V);
            double weight = 0.01 * StdRandom.uniform(100);
            DirectedEdge e = new DirectedEdge(v, w, weight);
            addEdge(e);
        }
    }

    public EdgeWeightedDigraph(In in) {
        if (in == null) throw new IllegalArgumentException("argument is null");
        try {
            this.V = in.readInt();
            if (V < 0) throw new IllegalArgumentException("number of vertices in a Digraph must be nonnegative");
            indegree = new int[V];
            adj = (Bag<DirectedEdge>[]) new Bag[V];
            for (int v = 0; v < V; v++) {
                adj[v] = new Bag<DirectedEdge>();
            }

            int E = in.readInt();
            if (E < 0) throw new IllegalArgumentException("Number of edges must be nonnegative");
            for (int i = 0; i < E; i++) {
                int v = in.readInt();
                int w = in.readInt();
                validateVertex(v);
                validateVertex(w);
                double weight = in.readDouble();
                addEdge(new DirectedEdge(v, w, weight));
            }
        }
        catch (NoSuchElementException e) {
            throw new IllegalArgumentException("invalid input format in EdgeWeightedDigraph constructor", e);
        }
    }

    public EdgeWeightedDigraph(EdgeWeightedDigraph G) {
        this(G.V());
        this.E = G.E();
        for (int v = 0; v < G.V(); v++)
            this.indegree[v] = G.indegree(v);
        for (int v = 0; v < G.V(); v++) {
            // reverse so that adjacency list is in same order as original
            Stack<DirectedEdge> reverse = new Stack<DirectedEdge>();
            for (DirectedEdge e : G.adj[v]) {
                reverse.push(e);
            }
            for (DirectedEdge e : reverse) {
                adj[v].add(e);
            }
        }
    }

    public int V() {
        return V;
    }

    public int E() {
        return E;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    public void addEdge(DirectedEdge e) {
        int v = e.from();
        int w = e.to();
        validateVertex(v);
        validateVertex(w);
        adj[v].add(e);
        indegree[w]++;
        E++;
    }

    public Iterable<DirectedEdge> adj(int v) {
        validateVertex(v);
        return adj[v];
    }

    public int outdegree(int v) {
        validateVertex(v);
        return adj[v].size();
    }

    public int indegree(int v) {
        validateVertex(v);
        return indegree[v];
    }

    public Iterable<DirectedEdge> edges() {
        Bag<DirectedEdge> list = new Bag<DirectedEdge>();
        for (int v = 0; v < V; v++) {
            for (DirectedEdge e : adj(v)) {
                list.add(e);
            }
        }
        return list;
    }

    public String toString() {
        StringBuilder s = new StringBuilder();
        s.append(V + " " + E + NEWLINE);
        for (int v = 0; v < V; v++) {
            s.append(v + ": ");
            for (DirectedEdge e : adj[v]) {
                s.append(e + "  ");
            }
            s.append(NEWLINE);
        }
        return s.toString();
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        EdgeWeightedDigraph G = new EdgeWeightedDigraph(in);
        StdOut.println(G);
    }

}

3.最短路径的Dijkstra算法

package graph;

import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.IndexMinPQ;
import edu.princeton.cs.algs4.Stack;
import edu.princeton.cs.algs4.StdOut;

public class DijkstraSP {
    private double[] distTo;          // distTo[v] = distance  of shortest s->v path
    private DirectedEdge[] edgeTo;    // edgeTo[v] = last edge on shortest s->v path
    private IndexMinPQ<Double> pq;    // priority queue of vertices

    public DijkstraSP(EdgeWeightedDigraph G, int s) {
        for (DirectedEdge e : G.edges()) {
            if (e.weight() < 0)
                throw new IllegalArgumentException("edge " + e + " has negative weight");
        }

        distTo = new double[G.V()];
        edgeTo = new DirectedEdge[G.V()];

        validateVertex(s);

        for (int v = 0; v < G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        distTo[s] = 0.0;

        // relax vertices in order of distance from s
        pq = new IndexMinPQ<Double>(G.V());
        pq.insert(s, distTo[s]);
        while (!pq.isEmpty()) {
            int v = pq.delMin();
            for (DirectedEdge e : G.adj(v))
                relax(e);
        }

        // check optimality conditions
        assert check(G, s);
    }

    // relax edge e and update pq if changed
    private void relax(DirectedEdge e) {
        int v = e.from(), w = e.to();
        if (distTo[w] > distTo[v] + e.weight()) {
            distTo[w] = distTo[v] + e.weight();
            edgeTo[w] = e;
            if (pq.contains(w)) pq.decreaseKey(w, distTo[w]);
            else                pq.insert(w, distTo[w]);
        }
    }

    public double distTo(int v) {
        validateVertex(v);
        return distTo[v];
    }

    public boolean hasPathTo(int v) {
        validateVertex(v);
        return distTo[v] < Double.POSITIVE_INFINITY;
    }

    public Iterable<DirectedEdge> pathTo(int v) {
        validateVertex(v);
        if (!hasPathTo(v)) return null;
        Stack<DirectedEdge> path = new Stack<DirectedEdge>();
        for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()]) {
            path.push(e);
        }
        return path;
    }


    // check optimality conditions:
    // (i) for all edges e:            distTo[e.to()] <= distTo[e.from()] + e.weight()
    // (ii) for all edge e on the SPT: distTo[e.to()] == distTo[e.from()] + e.weight()
    private boolean check(EdgeWeightedDigraph G, int s) {

        // check that edge weights are nonnegative
        for (DirectedEdge e : G.edges()) {
            if (e.weight() < 0) {
                System.err.println("negative edge weight detected");
                return false;
            }
        }

        // check that distTo[v] and edgeTo[v] are consistent
        if (distTo[s] != 0.0 || edgeTo[s] != null) {
            System.err.println("distTo[s] and edgeTo[s] inconsistent");
            return false;
        }
        for (int v = 0; v < G.V(); v++) {
            if (v == s) continue;
            if (edgeTo[v] == null && distTo[v] != Double.POSITIVE_INFINITY) {
                System.err.println("distTo[] and edgeTo[] inconsistent");
                return false;
            }
        }

        // check that all edges e = v->w satisfy distTo[w] <= distTo[v] + e.weight()
        for (int v = 0; v < G.V(); v++) {
            for (DirectedEdge e : G.adj(v)) {
                int w = e.to();
                if (distTo[v] + e.weight() < distTo[w]) {
                    System.err.println("edge " + e + " not relaxed");
                    return false;
                }
            }
        }

        // check that all edges e = v->w on SPT satisfy distTo[w] == distTo[v] + e.weight()
        for (int w = 0; w < G.V(); w++) {
            if (edgeTo[w] == null) continue;
            DirectedEdge e = edgeTo[w];
            int v = e.from();
            if (w != e.to()) return false;
            if (distTo[v] + e.weight() != distTo[w]) {
                System.err.println("edge " + e + " on shortest path not tight");
                return false;
            }
        }
        return true;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        int V = distTo.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        EdgeWeightedDigraph G = new EdgeWeightedDigraph(in);
        int s = Integer.parseInt(args[1]);

        // compute shortest paths
        DijkstraSP sp = new DijkstraSP(G, s);

        for (int t = 0; t < G.V(); t++) {
            if (sp.hasPathTo(t)) {
                StdOut.printf("%d to %d (%.2f)  ", s, t, sp.distTo(t));
                for (DirectedEdge e : sp.pathTo(t)) {
                    StdOut.print(e + "   ");
                }
                StdOut.println();
            }
            else {
                StdOut.printf("%d to %d         no path\n", s, t);
            }
        }
    }
}

4.无环加权有向图的最短路径算法

package graph;

import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.Stack;
import edu.princeton.cs.algs4.StdOut;

public class AcyclicSP {
    private double[] distTo;         // distTo[v] = distance  of shortest s->v path
    private DirectedEdge[] edgeTo;   // edgeTo[v] = last edge on shortest s->v path

    public AcyclicSP(EdgeWeightedDigraph G, int s) {
        distTo = new double[G.V()];
        edgeTo = new DirectedEdge[G.V()];

        validateVertex(s);

        for (int v = 0; v < G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        distTo[s] = 0.0;

        // visit vertices in topological order
        Topological topological = new Topological(G);
        if (!topological.hasOrder())
            throw new IllegalArgumentException("Digraph is not acyclic.");
        for (int v : topological.order()) {
            for (DirectedEdge e : G.adj(v))
                relax(e);
        }
    }

    // relax edge e
    private void relax(DirectedEdge e) {
        int v = e.from(), w = e.to();
        if (distTo[w] > distTo[v] + e.weight()) {
            distTo[w] = distTo[v] + e.weight();
            edgeTo[w] = e;
        }
    }

    public double distTo(int v) {
        validateVertex(v);
        return distTo[v];
    }

    public boolean hasPathTo(int v) {
        validateVertex(v);
        return distTo[v] < Double.POSITIVE_INFINITY;
    }

    public Iterable<DirectedEdge> pathTo(int v) {
        validateVertex(v);
        if (!hasPathTo(v)) return null;
        Stack<DirectedEdge> path = new Stack<DirectedEdge>();
        for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()]) {
            path.push(e);
        }
        return path;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        int V = distTo.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        int s = Integer.parseInt(args[1]);
        EdgeWeightedDigraph G = new EdgeWeightedDigraph(in);

        // find shortest path from s to each other vertex in DAG
        AcyclicSP sp = new AcyclicSP(G, s);
        for (int v = 0; v < G.V(); v++) {
            if (sp.hasPathTo(v)) {
                StdOut.printf("%d to %d (%.2f)  ", s, v, sp.distTo(v));
                for (DirectedEdge e : sp.pathTo(v)) {
                    StdOut.print(e + "   ");
                }
                StdOut.println();
            }
            else {
                StdOut.printf("%d to %d         no path\n", s, v);
            }
        }
    }
}