1.前言
pta第四次作业总共有3题,题量不是很多。其中,1、3题比较简单,第二题难度较大,第1题考察的正则表达式,第3题考察的是类的使用,第2题考查了关于四边形的算法,正则表达式以及类的使用,难度较大。
pta第五次作业总共有2题,实际上2题都是关于五边形的算法,可以看作为1题,题目难度很难,主要是关于五边形(多边形)的算法和正则表达式。
期中作业总共有3题,题量不是很多。3题层层递进,每题在前一题的基础上有所增加,整体难度不难。第一题考察的是类设计方面的知识,难度低,只需要根据题目给出的类图以及题意,使用Java类设计的方法和语法语句就能够完成。第二题考察的是继承与多态方面的知识,难度较低。第三题考察的是容器类方面的知识,创建一个容器存入Element类对象,根据类图和题意,创建相应方法能够完成该题目。
2.设计与分析
7-2 点线形系列4-凸四边形的计算
用户输入一组选项和数据,进行与四边形有关的计算。
以下四边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
1:输入四个点坐标,判断是否是四边形、平行四边形,判断结果输出true/false,结果之间以一个英文空格符分隔。
2:输入四个点坐标,判断是否是菱形、矩形、正方形,判断结果输出true/false,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
3:输入四个点坐标,判断是凹四边形(false)还是凸四边形(true),输出四边形周长、面积,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
4:输入六个点坐标,前两个点构成一条直线,后四个点构成一个四边形或三角形,输出直线与四边形(也可能是三角形)相交的交点数量。如果交点有两个,再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积(不换行)。若直线与四边形或三角形的一条边线重合,输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入,输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况:假设三角形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z 不与xy都相邻,如z x y s、x z s y、x s z y
5:输入五个点坐标,输出第一个是否在后四个点所构成的四边形(限定为凸四边形,不考虑凹四边形)或三角形(判定方法见选项4)的内部(若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。如果点在多边形的某条边上,输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形,输出"not a quadrilateral or triangle"。
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
注意:输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
选项1、2、3中,若四边形四个点中有重合点,输出"points coincide"。
选项4中,若前两个输入线的点重合,输出"points coincide"。
输入样例1:
选项1,点重合。例如:
1:-1,-1 -1,-1 1,2 1,-2
输出样例:
在这里给出相应的输出。例如:
points coincide
输入样例2:
不符合基本格式。例如:
1:-1,-1 1,2 -1,1 ++1,0
输出样例:
在这里给出相应的输出。例如:
Wrong Format
输入样例3:
选项1,输入点数量不对。例如:
1:-1,-1 -1,2
输出样例:
在这里给出相应的输出。例如:
wrong number of points
输入样例4:
选项1,正确输入判断。例如:
1:-1,-1 -1,1 1,2 1,-2
输出样例:
在这里给出相应的输出。例如:
true false
输入样例5:
选项2,输入点不构成四边形。例如:
2:10,10 1,1 0,0 1,20
输出样例:
在这里给出相应的输出。例如:
not a quadrilateral
输入样例6:
选项2,正方形。例如:
2:0,0 0,80 80,80 80,0
输出样例:
在这里给出相应的输出。例如:
true true true
输入样例7:
选项2。例如:
2:0,0 -10,80 0,160 -10,80
输出样例:
在这里给出相应的输出。例如:
not a quadrilateral
输入样例8:
选项3,凸四边形。例如:
3:-1,-1 -1,1 1,2 1,-2
输出样例:
在这里给出相应的输出。例如:
true 10.472 6.0
输入样例9:
选项3,。例如:
3:0,0 -10,100 0,99 10,100
输出样例:
在这里给出相应的输出。例如:
false 221.097 990.0
我的代码:
import javax.print.DocFlavor; import java.util.Scanner; import java.text.DecimalFormat; public class Main { public static void main(String[] args) { DecimalFormat d = new DecimalFormat("0.0##"); Scanner input = new Scanner(System.in); String str = input.nextLine(); char[] a = new char[50]; if (!str.matches("^[1-5]:(([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)),([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)) )*(([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)),([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?))) *" )) System.out.println("Wrong Format"); else { a = str.toCharArray(); if (a[1] == ':') { String[] str1 = str.split(":"); String[] str2 = str1[1].split(" "); double x1, y1, x2, y2, x3, y3, x4, y4, x5, y5, x6, y6; boolean b = true; for (int i = 0; i < str2.length; i++) { b = geshi(str2[i]); if (!b) break; } switch (a[0]) { case '1': if (str2.length == 4) { String[] s0 = str2[0].split(",");//x1,y1 String[] s1 = str2[1].split(",");//x2,y2 String[] s2 = str2[2].split(",");//x3,y3 String[] s3 = str2[3].split(",");//x4,y4 x1 = Double.parseDouble(s0[0]); y1 = Double.parseDouble(s0[1]); x2 = Double.parseDouble(s1[0]); y2 = Double.parseDouble(s1[1]); x3 = Double.parseDouble(s2[0]); y3 = Double.parseDouble(s2[1]); x4 = Double.parseDouble(s3[0]); y4 = Double.parseDouble(s3[1]); dian A = new dian(x1, y1); dian B = new dian(x2, y2); dian C = new dian(x3, y3); dian D = new dian(x4, y4); sibianxing m = new sibianxing(); if (A.chonghe(B) || A.chonghe(C) || A.chonghe(D) || B.chonghe(C) || B.chonghe(D) || C.chonghe(D)) System.out.println("points coincide"); else { if (m.panduan(A, B, C, D)) System.out.print("true "); else System.out.print("false "); if (m.pingxing(A, B, C, D)) System.out.println("true"); else System.out.println("false"); } } else System.out.println("wrong number of points"); break; case '2': if (str2.length == 4) { String[] s0 = str2[0].split(",");//x1,y1 String[] s1 = str2[1].split(",");//x2,y2 String[] s2 = str2[2].split(",");//x3,y3 String[] s3 = str2[3].split(",");//x4,y4 x1 = Double.parseDouble(s0[0]); y1 = Double.parseDouble(s0[1]); x2 = Double.parseDouble(s1[0]); y2 = Double.parseDouble(s1[1]); x3 = Double.parseDouble(s2[0]); y3 = Double.parseDouble(s2[1]); x4 = Double.parseDouble(s3[0]); y4 = Double.parseDouble(s3[1]); dian A = new dian(x1, y1); dian B = new dian(x2, y2); dian C = new dian(x3, y3); dian D = new dian(x4, y4); sibianxing m = new sibianxing(); if (!m.panduan(A, B, C, D)) System.out.println("not a quadrilateral"); else { if (!A.chonghe(B) || !A.chonghe(C) || !A.chonghe(D) || !B.chonghe(C) || !B.chonghe(D) || !C.chonghe(D)) { if (m.lingxing(A, B, C, D)) System.out.print("true "); else System.out.print("false "); if (m.juxing(A, B, C, D)) System.out.print("true "); else System.out.print("false "); if (m.zhengfangxing(A, B, C, D)) System.out.println("true"); else System.out.println("false"); } else System.out.println("points coincide"); } } else System.out.println("wrong number of points"); break; case '3': if (str2.length == 4) { String[] s0 = str2[0].split(",");//x1,y1 String[] s1 = str2[1].split(",");//x2,y2 String[] s2 = str2[2].split(",");//x3,y3 String[] s3 = str2[3].split(",");//x4,y4 x1 = Double.parseDouble(s0[0]); y1 = Double.parseDouble(s0[1]); x2 = Double.parseDouble(s1[0]); y2 = Double.parseDouble(s1[1]); x3 = Double.parseDouble(s2[0]); y3 = Double.parseDouble(s2[1]); x4 = Double.parseDouble(s3[0]); y4 = Double.parseDouble(s3[1]); dian A = new dian(x1, y1); dian B = new dian(x2, y2); dian C = new dian(x3, y3); dian D = new dian(x4, y4); sibianxing m = new sibianxing(); if (A.chonghe(B) || A.chonghe(C) || A.chonghe(D) || B.chonghe(C) || B.chonghe(D) || C.chonghe(D)) System.out.println("points coincide"); else { if (m.panduan(A, B, C, D)) { if (m.aotu(A, B, C, D)) System.out.print("true "); else System.out.print("false "); System.out.println(d.format(m.zhouchang(A, B, C, D)) + " " + d.format(m.mianji(A, B, C, D))); } else System.out.println("not a quadrilateral"); } } else System.out.println("wrong number of points"); break; case '4': if (str2.length == 6) { String[] s0 = str2[0].split(",");//x1,y1 String[] s1 = str2[1].split(",");//x2,y2 String[] s2 = str2[2].split(",");//x3,y3 String[] s3 = str2[3].split(",");//x4,y4 String[] s4 = str2[4].split(",");//x5,y5 String[] s5 = str2[5].split(",");//x6,y6 x1 = Double.parseDouble(s0[0]); y1 = Double.parseDouble(s0[1]); x2 = Double.parseDouble(s1[0]); y2 = Double.parseDouble(s1[1]); x3 = Double.parseDouble(s2[0]); y3 = Double.parseDouble(s2[1]); x4 = Double.parseDouble(s3[0]); y4 = Double.parseDouble(s3[1]); x5 = Double.parseDouble(s4[0]); y5 = Double.parseDouble(s4[1]); x6 = Double.parseDouble(s5[0]); y6 = Double.parseDouble(s5[1]); dian A = new dian(x1, y1); dian B = new dian(x2, y2); dian C = new dian(x3, y3); dian D = new dian(x4, y4); dian E = new dian(x5, y5); dian F = new dian(x6, y6); xian l = new xian(); sibianxing m = new sibianxing(); sanjiaoxing n = new sanjiaoxing(); if (A.x == B.x && A.y == B.y) System.out.println("points coincide"); else if (l.zhixianchonghe(A, B, C, D) || l.zhixianchonghe(A, B, D, E) || l.zhixianchonghe(A, B, E, F) || l.zhixianchonghe(A, B, F, C)) { System.out.println("The line is coincide with one of the lines"); return; } else if (m.panduan(C, D, E, F)) { if (m.zhixiansibianxingjiaodian(A, B, C, D, E, F) == 0) System.out.println("0"); else if (m.zhixiansibianxingjiaodian(A, B, C, D, E, F) == 1) System.out.println("1"); else if (m.zhixiansibianxingjiaodian(A, B, C, D, E, F) == 2) System.out.println("2 "); } else if (m.sanjiaoxing(C, D, E, F)) { } else if (m.sanjiaoxing(D, E, F, C)) { } else if (m.sanjiaoxing(E, F, C, D)) { } else if (m.sanjiaoxing(F, E, C, D)) { } else System.out.println("not a quadrilateral or triangle"); } else System.out.println("wrong number of points"); break; case '5': if (str2.length == 5) { String[] s0 = str2[0].split(",");//x1,y1 String[] s1 = str2[1].split(",");//x2,y2 String[] s2 = str2[2].split(",");//x3,y3 String[] s3 = str2[3].split(",");//x4,y4 String[] s4 = str2[4].split(",");//x5,y5 x1 = Double.parseDouble(s0[0]); y1 = Double.parseDouble(s0[1]); x2 = Double.parseDouble(s1[0]); y2 = Double.parseDouble(s1[1]); x3 = Double.parseDouble(s2[0]); y3 = Double.parseDouble(s2[1]); x4 = Double.parseDouble(s3[0]); y4 = Double.parseDouble(s3[1]); x5 = Double.parseDouble(s4[0]); y5 = Double.parseDouble(s4[1]); dian A = new dian(x1, y1); dian B = new dian(x2, y2); dian C = new dian(x3, y3); dian D = new dian(x4, y4); dian E = new dian(x5, y5); xian l = new xian(); sibianxing m = new sibianxing(); sanjiaoxing n = new sanjiaoxing(); if (!m.panduan(B, C, D, E) && !m.sanjiaoxing(B, C, D, E) && !m.sanjiaoxing(C, D, E, B) && !m.sanjiaoxing(D, E, B, C) && !m.sanjiaoxing(E, B, C, D) && !B.chonghe(C) && !B.chonghe(D) && !B.chonghe(E) && !D.chonghe(C) && !E.chonghe(C) && !D.chonghe(E)) System.out.println("not a quadrilateral or triangle"); if (m.panduan(B, C, D, E)) { if (l.dianzaixianduanshang(A, B, C) || l.dianzaixianduanshang(A, C, D) || l.dianzaixianduanshang(A, D, E) || l.dianzaixianduanshang(A, E, B)) System.out.println("on the quadrilateral"); else if (m.dianzaimiannei(B, C, D, E, A)) System.out.println("in the quadrilateral"); else System.out.println("outof the quadrilateral"); } else if // (m.sanjiaoxing(B, C, D, E)) { // dian[] dians = m.fanhuishanjiaoxing(B, C, D, E); // n.shuchudianmian(A, dians[0], dians[1], dians[2]); // return; (m.sanjiaoxing(B, C, D, E) || C.chonghe(E)) { n.shuchudianmian(A, B, D, E); } else if (m.sanjiaoxing(C, D, E, B) || D.chonghe(B)) { n.shuchudianmian(A, C, E, B); } else if (m.sanjiaoxing(D, E, B, C) || E.chonghe(C)) { n.shuchudianmian(A, D, B, C); } else if (m.sanjiaoxing(E, B, C, D) || B.chonghe(D)) { n.shuchudianmian(A, E, C, D); } } else System.out.println("wrong number of points"); break; default: System.out.println("Wrong Format"); break; } } else System.out.println("Wrong Format"); } } public static boolean geshi(String a) { String[] b = a.split(" "); boolean flag = true; String regex = "^[+-]?(0|(0\\\\.\\\\d+)?|[1-9][0-9]*(\\\\.\\\\d+)?)$"; for (int i = 0; i < b.length; i++) { flag = b[i].matches(regex); if (!flag) break; } if (flag) { return true; } else return false; } } class dian { double x, y; dian(double x, double y) { this.x = x; this.y = y; } boolean chonghe(dian p2) { if (this.x == p2.x && p2.y == this.y) return true; else return false; } double changdu(dian p2) { double d1 = Math.pow(p2.x - this.x, 2); double d2 = Math.pow(p2.y - this.y, 2); return Math.pow(d2 + d1, 0.5); } double k(dian p2) { return (y - p2.y) / (x - p2.x); } } class xian { //线段AC与BD的交点是否在线段上 boolean xianduanjioadian(dian A, dian B, dian C, dian D) { double x, y; y = (B.x * C.y * D.y - D.x * B.y * C.y - A.y * B.x * D.y + D.x * B.y * A.y + C.x * A.y * D.y - A.x * C.y * D.y - C.x * B.y * A.y + A.x * B.y * C.y) / (D.y * C.x - A.x * D.y - B.y * C.x + A.x * B.y + B.x * C.y - D.x * C.y - A.y * B.x + A.y * D.x); x = (D.y * (C.x - A.x) * (B.x - D.x) - A.y * (C.x - A.x) * (B.x - D.x) + A.x * (C.y - A.y) * (B.x - D.x) + D.x * (D.y - B.y) * (C.x - A.x)) / ((C.y - A.y) * (B.x - D.x) + (D.y - B.y) * (C.x - A.x)); if (B.x > D.x && A.x > C.x) { if (x < B.x && x > D.x && x < A.x && x > C.x) return true; else return false; } if (B.x < D.x && A.x > C.x) { if (x > B.x && x < D.x && x < A.x && x > C.x) return true; else return false; } if (B.x < D.x && A.x < C.x) { if (x > B.x && x < D.x && x > A.x && x < C.x) return true; else return false; } if (B.x > D.x && A.x < C.x) { if (x < B.x && x > D.x && x > A.x && x < C.x) return true; else return false; } if (B.x < D.x && A.x > C.x) { if (x > B.x && x < D.x && x > A.x && x < C.x) return true; else return false; } else return false; } dian xianduanjioafanhuidian(dian A, dian B, dian C, dian D) { double x, y; y = (B.x * C.y * D.y - D.x * B.y * C.y - A.y * B.x * D.y + D.x * B.y * A.y + C.x * A.y * D.y - A.x * C.y * D.y - C.x * B.y * A.y + A.x * B.y * C.y) / (D.y * C.x - A.x * D.y - B.y * C.x + A.x * B.y + B.x * C.y - D.x * C.y - A.y * B.x + A.y * D.x); x = (D.y * (C.x - A.x) * (B.x - D.x) - A.y * (C.x - A.x) * (B.x - D.x) + A.x * (C.y - A.y) * (B.x - D.x) + D.x * (D.y - B.y) * (C.x - A.x)) / ((C.y - A.y) * (B.x - D.x) + (D.y - B.y) * (C.x - A.x)); dian dian = new dian(x, y); return dian; } //交点是否在线段CD上 boolean jiaodianzaixianduanshang(dian A, dian B, dian C, dian D) { if (C.x > D.x) { if (xianduanjioafanhuidian(A, B, C, D).x > D.x && xianduanjioafanhuidian(A, B, C, D).x < C.x) return true; else return false; } else if (C.x < D.x) { if (xianduanjioafanhuidian(A, B, C, D).x < D.x && xianduanjioafanhuidian(A, B, C, D).x > C.x) return true; else return false; } else return false; } boolean dianzaixiangshang(dian A, dian B, dian C) { if (A.x == B.x && B.x == C.x && A.x == C.x) return true; else { if (Math.abs(A.k(B) - B.k(C)) < 1e-6) return true; else return false; } } //点A在线段BC上 boolean dianzaixianduanshang(dian A, dian B, dian C) { if (dianzaixiangshang(A, B, C)) { if (B.x < C.x) if (B.x <= A.x && A.x <= C.x) return true; else return false; else if (B.x > C.x) if (B.x >= A.x && A.x >= C.x) return true; else return false; else return false; } else return false; } boolean zhixianchonghe(dian A, dian B, dian C, dian D) { if ((Math.abs(A.k(B) - C.k(D)) < 1e-6 && dianzaixiangshang(A, C, D))) return true; else return false; } } class sanjiaoxing { double mianji(dian A, dian B, dian C) { double a, b, c, p; a = C.changdu(B); b = A.changdu(C); c = A.changdu(B); p = (A.changdu(B) + C.changdu(B) + A.changdu(C)) / 2; return Math.pow(p * (p - a) * (p - b) * (p - c), 0.5); } //点A是否在三角形BCD内 boolean dianzaimiannei(dian A, dian B, dian C, dian D) { if (Math.abs((mianji(A, B, D) + mianji(A, C, D) + mianji(A, B, C)) - mianji(B, C, D)) < 1e-6) return true; else return false; } //点A与三角形的关系 void shuchudianmian(dian A, dian B, dian C, dian D) { xian l = new xian(); if (l.dianzaixianduanshang(A, B, C) || l.dianzaixianduanshang(A, B, D) || l.dianzaixianduanshang(A, C, D)) System.out.println("on the triangle"); else if (dianzaimiannei(A, B, C, D)) System.out.println("in the triangle"); else System.out.println("outof the triangle"); } } class sibianxing { xian l1 = new xian(); boolean panduan(dian A, dian B, dian C, dian D) { if (!l1.xianduanjioadian(A, C, B, D) && !l1.xianduanjioadian(C, A, B, D) && Math.abs(A.k(B) - C.k(B)) > 1e-6 && Math.abs(C.k(B) - C.k(D)) > 1e-6 && Math.abs(C.k(D) - A.k(D)) > 1e-6) { return true; } else return false; } boolean pingxing(dian A, dian B, dian C, dian D) { if ((Math.abs((A.x + C.x) - (B.x + D.x)) < 1e-6) && (Math.abs((A.y + C.y) - (B.y + D.y)) < 1e-6)) { return true; } else return false; } boolean lingxing(dian A, dian B, dian C, dian D) { if (A.changdu(B) == A.changdu(D) && A.changdu(D) == B.changdu(C) && A.changdu(B) == D.changdu(C)) return true; else return false; } boolean juxing(dian A, dian B, dian C, dian D) { if (A.changdu(C) == B.changdu(D)) return true; else return false; } boolean zhengfangxing(dian A, dian B, dian C, dian D) { if (lingxing(A, B, C, D) && juxing(A, B, C, D)) return true; else return false; } boolean aotu(dian A, dian B, dian C, dian D) { sanjiaoxing sjx = new sanjiaoxing(); double s1, s2; s1 = (sjx.mianji(A, B, C) + sjx.mianji(A, C, D)); s2 = (sjx.mianji(A, B, D) + sjx.mianji(B, C, D)); if (Math.abs(s1 - s2) < 1e-6) return true; else return false; } double zhouchang(dian A, dian B, dian C, dian D) { return A.changdu(B) + B.changdu(C) + C.changdu(D) + D.changdu(A); } double mianji(dian A, dian B, dian C, dian D) { sanjiaoxing sjx = new sanjiaoxing(); double s1, s2; s1 = (sjx.mianji(A, B, C) + sjx.mianji(A, C, D)); s2 = (sjx.mianji(A, B, D) + sjx.mianji(B, C, D)); if (Math.abs(s1 - s2) < 1e-6) return s1; else if (s1 > s2) return s2; else return s1; } //点E是否在四边形面内 boolean dianzaimiannei(dian A, dian B, dian C, dian D, dian E) { sanjiaoxing a = new sanjiaoxing(); if (Math.abs((a.mianji(A, B, E) + a.mianji(B, C, E) + a.mianji(C, D, E) + a.mianji(D, A, E)) - mianji(A, B, C, D)) < 1e-6) return true; else return false; } //是否能构成三角形 boolean sanjiaoxing(dian A, dian B, dian C, dian D) { xian l = new xian(); // if (ac.dianzaixianduanshang(A, B, D) || ac.dianzaixianduanshang(C, B, D) || ac.dianzaixianduanshang(B, A, C) || ac.dianzaixianduanshang(D, A, C)) // return true; // return false; if (!A.chonghe(B) || !A.chonghe(C) || !A.chonghe(D) || !B.chonghe(C) || !B.chonghe(D) || !C.chonghe(D)) if (l.dianzaixianduanshang(B, A, C) && Math.abs((A.changdu(B) + B.changdu(C)) - A.changdu(C)) <= 1e-6) return true; else return false; else if (B.chonghe(D)) return true; else return false; } dian[] fanhuishanjiaoxing(dian A, dian B, dian C, dian D) { dian[] dians = new dian[3]; xian ac = new xian(); int num = 0; if (!ac.dianzaixianduanshang(A, B, D)) dians[num++] = A; if (ac.dianzaixianduanshang(C, B, D)) dians[num++] = C; if (ac.dianzaixianduanshang(B, A, C)) dians[num++] = B; if (ac.dianzaixianduanshang(D, A, C)) dians[num++] = D; return dians; } //点A与点B重合构成三角形A(B)CD boolean chsanjiaoxing(dian A, dian B, dian C, dian D) { if (A.chonghe(B)) return true; else return false; } int zhixiansibianxingjiaodian(dian A, dian B, dian C, dian D, dian E, dian F) { int i = 0; if (l1.jiaodianzaixianduanshang(A, B, C, D)) i++; else if (l1.jiaodianzaixianduanshang(A, B, D, E)) i++; else if (l1.jiaodianzaixianduanshang(A, B, E, F)) i++; else if (l1.jiaodianzaixianduanshang(A, B, F, C)) i++; return i; } }


分析:本题先用正则表达式判断是否输入正确,判断四边形可以采用邻边相交,对边不相交。判断凹凸性可以判断对角线切割的两个三角形面积和是否等于四边形面积,若不相等,则为凹,反之,则为凸。判断交点可以不用射线法,可以线的切割点有几个在线上。点与面的位置判断,先判断点是否在线上,再用点与各边组成的三角形的面积是否等于四边形的面积是否相等,相等则在面内,反之,在面外。
7-1 点线形系列5-凸五边形的计算-1
用户输入一组选项和数据,进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
1:输入五个点坐标,判断是否是五边形,判断结果输出true/false。
2:输入五个点坐标,判断是凹五边形(false)还是凸五边形(true),如果是凸五边形,则再输出五边形周长、面积,结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形,输出"not a pentagon"
3:输入七个点坐标,前两个点构成一条直线,后五个点构成一个凸五边形、凸四边形或凸三角形,输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个,再按面积从小到大输出被直线分割成两部分的面积(不换行)。若直线与多边形形的一条边线重合,输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入,若前两点重合,输出"points coincide"。
以上3选项中,若输入的点无法构成多边形,则输出"not a polygon"。输入的五个点坐标可能存在冗余,假设多边形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如:x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z不与xy都相邻,如:z x y s、x z s y、x s z y
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
注意:输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
输入样例1:
选项1,点重合。例如:
1:-1,-1 1,2 -1,1 1,0
输出样例:
在这里给出相应的输出。例如:
wrong number of points
我的代码:
import java.util.Scanner;
import java.text.DecimalFormat;
public class Main {
public static void main(String[] args) {
DecimalFormat d = new DecimalFormat("0.0##");
Scanner input = new Scanner(System.in);
String str = input.nextLine();
char[] a = new char[50];
if (!str.matches("^[1-5]:(([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)),([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)) )*(([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)),([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?))) *"
))
System.out.println("Wrong Format");
else {
a = str.toCharArray();
if (a[1] == ':') {
String[] str1 = str.split(":");
String[] str2 = str1[1].split(" ");
double x1, y1, x2, y2, x3, y3, x4, y4, x5, y5, x6, y6, x7, y7;
boolean b = true;
for (int i = 0; i < str2.length; i++) {
b = geshi(str2[i]);
if (!b)
break;
}
switch (a[0]) {
case '1':
if (str2.length == 5) {
String[] s0 = str2[0].split(",");//x1,y1
String[] s1 = str2[1].split(",");//x2,y2
String[] s2 = str2[2].split(",");//x3,y3
String[] s3 = str2[3].split(",");//x4,y4
String[] s4 = str2[4].split(",");//x5,y5
x1 = Double.parseDouble(s0[0]);
y1 = Double.parseDouble(s0[1]);
x2 = Double.parseDouble(s1[0]);
y2 = Double.parseDouble(s1[1]);
x3 = Double.parseDouble(s2[0]);
y3 = Double.parseDouble(s2[1]);
x4 = Double.parseDouble(s3[0]);
y4 = Double.parseDouble(s3[1]);
x5 = Double.parseDouble(s4[0]);
y5 = Double.parseDouble(s4[1]);
dian A = new dian(x1, y1);
dian B = new dian(x2, y2);
dian C = new dian(x3, y3);
dian D = new dian(x4, y4);
dian E = new dian(x5, y5);
xian AB = new xian(A, B);
xian BC = new xian(B, C);
xian CD = new xian(C, D);
xian DE = new xian(D, E);
xian EA = new xian(E, A);
wubianxing m = new wubianxing(A, B, C, D, E);
if (!A.chonghe(B) && !B.chonghe(C) && !C.chonghe(D) && !D.chonghe(E)) {
if (m.panduan())
System.out.println("true");
else
System.out.println("false");
} else
System.out.println("false");
} else
System.out.println("wrong number of points");
break;
case '2':
if (str2.length == 5) {
String[] s0 = str2[0].split(",");//x1,y1
String[] s1 = str2[1].split(",");//x2,y2
String[] s2 = str2[2].split(",");//x3,y3
String[] s3 = str2[3].split(",");//x4,y4
String[] s4 = str2[4].split(",");//x5,y5
x1 = Double.parseDouble(s0[0]);
y1 = Double.parseDouble(s0[1]);
x2 = Double.parseDouble(s1[0]);
y2 = Double.parseDouble(s1[1]);
x3 = Double.parseDouble(s2[0]);
y3 = Double.parseDouble(s2[1]);
x4 = Double.parseDouble(s3[0]);
y4 = Double.parseDouble(s3[1]);
x5 = Double.parseDouble(s4[0]);
y5 = Double.parseDouble(s4[1]);
dian A = new dian(x1, y1);
dian B = new dian(x2, y2);
dian C = new dian(x3, y3);
dian D = new dian(x4, y4);
dian E = new dian(x5, y5);
dian[] dians = new dian[]{A, B, C, D, E};
xian AB = new xian(A, B);
xian BC = new xian(B, C);
xian CD = new xian(C, D);
xian DE = new xian(D, E);
xian EA = new xian(E, A);
wubianxing m = new wubianxing(A, B, C, D, E);
if (m.panduan()) {
if (m.aotu()) {
System.out.print("true " + d.format(m.zhouchang()) + " " + d.format(m.mianji(dians)));
} else
System.out.println("false");
} else
System.out.println("not a pentagon");
} else
System.out.println("wrong number of points");
break;
case '3':
if (str2.length == 7) {
String[] s0 = str2[0].split(",");//x1,y1
String[] s1 = str2[1].split(",");//x2,y2
String[] s2 = str2[2].split(",");//x3,y3
String[] s3 = str2[3].split(",");//x4,y4
String[] s4 = str2[4].split(",");//x5,y5
String[] s5 = str2[5].split(",");//x6,y6
String[] s6 = str2[6].split(",");//x7,y7
x1 = Double.parseDouble(s0[0]);
y1 = Double.parseDouble(s0[1]);
x2 = Double.parseDouble(s1[0]);
y2 = Double.parseDouble(s1[1]);
x3 = Double.parseDouble(s2[0]);
y3 = Double.parseDouble(s2[1]);
x4 = Double.parseDouble(s3[0]);
y4 = Double.parseDouble(s3[1]);
x5 = Double.parseDouble(s4[0]);
y5 = Double.parseDouble(s4[1]);
x6 = Double.parseDouble(s5[0]);
y6 = Double.parseDouble(s5[1]);
x7 = Double.parseDouble(s6[0]);
y7 = Double.parseDouble(s6[1]);
dian A = new dian(x1, y1);
dian B = new dian(x2, y2);
dian C = new dian(x3, y3);
dian D = new dian(x4, y4);
dian E = new dian(x5, y5);
dian F = new dian(x6, y6);
dian G = new dian(x7, y7);
dian[] dians = new dian[]{C, D, E, F, G};
xian AB = new xian(A, B);
xian CD = new xian(C, D);
xian DE = new xian(D, E);
xian EF = new xian(E, F);
xian FG = new xian(F, G);
xian GC = new xian(G, C);
dbx m = new dbx(dians);
if (A.chonghe(B) )
System.out.println("points coincide");
else {
if (AB.zhixianchonghe(CD) &&AB.zhixianchonghe(DE) &&AB.zhixianchonghe(EF) &&AB.zhixianchonghe(FG) &&AB.zhixianchonghe(GC) )
System.out.println("The line is coincide with one of the lines");
else
m.zhixianqiege(AB);
}
} else
System.out.println("wrong number of points");
break;
default:
System.out.println("Wrong Format");
break;
}
} else
System.out.println("Wrong Format");
}
}
public static boolean geshi(String a) {
String[] b = a.split(" ");
boolean flag = true;
String regex = "^[+-]?(0|(0\\\\.\\\\d+)?|[1-9][0-9]*(\\\\.\\\\d+)?)$";
for (int i = 0; i < b.length; i++) {
flag = b[i].matches(regex);
if (!flag)
break;
}
if (flag) {
return true;
} else
return false;
}
}
class dian {
public double x, y;
public dian(double x, double y) {
this.x = x;
this.y = y;
}
boolean chonghe(dian dian) {
if (Math.abs(this.x - dian.x) < 1e-6 && Math.abs(this.y - dian.y) < 1e-6)
return true;
else return false;
}
boolean panduan(dian x, dian y) {
double x1, y1, x2, y2, x3, y3;
x1 = this.x - x.x;
y1 = x.y - this.y;
x2 = this.x - y.x;
y2 = y.y - this.y;
x3 = x.x - y.x;
y3 = y.y - x.y;
if (x1 * y2 - x2 * y1 > 0 && x2 * y3 - x3 * y2 > 0)
return true;
else return false;
}
boolean sandiangongxian(dian dian1, dian dian2) {
xian xian = new xian(this, dian2);
if (xian.dianzhaixianduanshang(dian1))
return true;
return false;
// if (Math.abs(((dian1.x - this.x ) * (dian2.y - this.y)) - (dian2.x - this.x) * (dian1.y) - this.y) < 1e-6)
// return true;
// else return false;
}
boolean is_in(dian[] dians, int k) {
int a = 0;
for (int i = 0; i < k; i++) {
if (this.x == dians[i].x && this.y == dians[i].y)
a++;
}
if (a == 0)
return false;
else return true;
}
}
class xian {
public dian x, y;
double k, b, cd;
boolean yes_k;
public xian(dian x, dian y) {
this.x = x;
this.y = y;
if (x.x == y.x) {
this.yes_k = false;
k = 99999;
b = x.x;
} else {
this.yes_k = true;
k = (x.y - y.y) / (x.x - y.x);
b = y.y - k * y.x;
}
cd = Math.pow((x.x - y.x) * (x.x - y.x) + (x.y - y.y) * (x.y - y.y), 0.5);
}
boolean dianzaixianshang(dian dian){
if(dian.y==dian.x*this.k+this.b)
return true;
else return false;
}
boolean xianjiao(xian l) {
if (!l.yes_k && !this.yes_k)
return false;
else if ((l.yes_k && !this.yes_k) || (this.yes_k && !l.yes_k))
return true;
else {
if (this.k == l.k)
return false;
else return true;
}
}
dian jiaodian(xian l) {
double x = 0.0, y = 0.0;
dian p = new dian(x, y);
if (this.xianjiao(l)) {
if (l.yes_k && this.yes_k) {
p.x = (l.b - this.b) / (this.k - l.k);
p.y = this.k * p.x + this.b;
} else if (!l.yes_k && this.yes_k) {
p.x = l.b;
p.y = this.k * l.b + this.b;
} else if (l.yes_k && !this.yes_k) {
p.x = this.b;
p.y = l.k * this.b + l.b;
}
return p;
}
return null;
}
boolean dianzhaixianduanshang(dian dian) {
if (yes_k)
return dian.x <= Math.max(this.x.x, this.y.x) && dian.x >= Math.min(this.x.x, this.y.x) && dian.y == this.k * dian.x + this.b;
else
return dian.y <= Math.max(this.x.y, this.y.y) && dian.y >= Math.min(this.x.y, this.y.y) && dian.x == this.b;
}
boolean xianduanxianjiao(xian l) {
if (xianjiao(l)) {
dian dian = jiaodian(l);
return l.dianzhaixianduanshang(dian) && this.dianzhaixianduanshang(dian);
}
return false;
}
//直线与线段l的交点
boolean xianxianduanjiaodian(xian l) {
if (this.xianjiao(l)) {
dian dian = jiaodian(l);
return l.dianzhaixianduanshang(dian);
}
return false;
}
// -1 0 1
int dianxianweizhi(dian dian) {
if (!yes_k) {
if (dian.x < b)
return 1;
else if (dian.x == b)
return 0;
else
return -1;
}
if (dian.y < (this.k * dian.x + b))
return 1;
else if (dian.y == (this.k * dian.x + b))
return 0;
else
return -1;
}
boolean zhixianchonghe(xian l){
if(dianzaixianshang(l.x)&&dianzaixianshang(l.y))
return true;
else return false;
}
}
class wubianxing {
dian A, B, C, D, E;
dian[] dians;
xian AB, BC, CD, DE, EA;
public wubianxing(dian A, dian B, dian C, dian D, dian E) {
this.A = A;
this.B = B;
this.C = C;
this.D = D;
this.E = E;
this.AB = new xian(A, B);
this.BC = new xian(B, C);
this.CD = new xian(C, D);
this.DE = new xian(D, E);
this.EA = new xian(E, A);
dians = new dian[]{A, B, C, D, E};
}
//判断是否能构成五边形
boolean panduan() {
if (!A.chonghe(B) && !A.chonghe(C) && !A.chonghe(D) && !A.chonghe(E) && !B.chonghe(C) && !B.chonghe(D) && !B.chonghe(E) && !C.chonghe(D) && !D.chonghe(E) && !D.chonghe(E)) {
if (!A.sandiangongxian(B, C) && !B.sandiangongxian(C, D) && !AB.xianduanxianjiao(DE) && !BC.xianduanxianjiao(DE) && !AB.xianduanxianjiao(CD) && !BC.xianduanxianjiao(EA) && !CD.xianduanxianjiao(EA)
&& !C.sandiangongxian(D, E) && !D.sandiangongxian(E, A) && !E.sandiangongxian(A, B)) {
return true;
} else return false;
} else return false;
}
//判断五边形凹凸
boolean aotu() {
if ((A.panduan(B, C) && B.panduan(C, D) && C.panduan(D, E) && D.panduan(E, A) && E.panduan(A, B)) || (!A.panduan(B, C) && !B.panduan(C, D) && !C.panduan(D, E) && !D.panduan(E, A) && !E.panduan(A, B)))
return true;
else return false;
}
double zhouchang() {
return AB.cd + BC.cd + CD.cd + DE.cd + EA.cd;
}
boolean chacheng(dian P, dian A, dian B) {
double d = (A.x - P.x) * (B.y - P.y) - (B.x - P.x) * (A.y - P.y);
if (d < 0) return true;
if (d > 0) return false;
else return false;
}
void chongpai(dian[] dians) {
double x = 0, y = 0;
for (int i = 0; i < dians.length - 1; i++) {
x += dians[i].x;
y += dians[i].y;
}
x = x / dians.length;
y = y / dians.length;
dian p = new dian(x, y);
dian t = null;
for (int i = 0; i < dians.length - 1; i++) {
for (int j = 0; j < dians.length - 1 - i; j++) {
if (chacheng(p, dians[j], dians[j + 1])) {
t = dians[j];
dians[j] = dians[j + 1];
dians[j + 1] = t;
}
}
}
}
double mianji(dian[] dians) {
int i = 0;
dian p1 = dians[i], p2 = dians[i + 1];
double result = 0;
while (p2 != dians[dians.length - 1]) {
result += (p1.x * p2.y) - (p1.y * p2.x);
i++;
p1 = dians[i];
p2 = dians[i + 1];
}
result += (p1.x * p2.y) - (p1.y * p2.x);
i++;
p1 = dians[i];
p2 = dians[0];
result += (p1.x * p2.y) - (p1.y * p2.x);
return Math.abs(result / 2);
}
public void panduantuxing(xian l) {
dian[] dians = {A, B, C, D, E};
dian[] ps = new dian[5];
int k = 0;
for (int i = 0; i < dians.length; i++) {
if (!dians[i].is_in(ps, k)) {
ps[k] = dians[i];
k++;
}
}
if(k==3){
sanjiaoxing sanjiaoxing = new sanjiaoxing(ps[0],ps[1],ps[2]);
sanjiaoxing.zhixianqiege(l);
}
}
}
class dbx {
dian[] dians;
xian[] xians;
DecimalFormat d = new DecimalFormat("0.0##");
public dbx(dian[] dians) {
this.dians = dians;
this.xians = new xian[dians.length];
for (int i = 0; i < dians.length; i++) {
xian xian = new xian(dians[i], dians[(i + 1) % dians.length]);
this.xians[i] = xian;
}
}
boolean is_dbx() {
int k = 0;
dian[] dians1 = new dian[dians.length];
for (int i = 0; i < dians.length; i++) {
if (!dians[i].is_in(dians1, k)) {
dians1[k] = dians[i];
k++;
}
}
if (k != dians.length)
return false;
if (this.dians.length < 3)
return false;
else if (dians.length == 3) {
xian xian = new xian(dians[0], dians[1]);
if (xian.dianzhaixianduanshang(dians[2]))
return false;
return true;
} else {
for (int i = 0; i < xians.length; i++) {
if (!xians[i].xianjiao(xians[(i + 1) % xians.length]))
return false;
}
for (int i = 0; i < xians.length; i++)
for (int j = 0; j < xians.length; j++) {
if (j != (i - 1 + xians.length) % xians.length && j != (i + 1) % xians.length && i != j)
if (xians[i].xianxianduanjiaodian(xians[j]))
return false;
}
}
return true;
}
void zhixianqiege(xian l) {
double s1, s2;
dian[] dians1 = new dian[5];
dian[] dians2 = new dian[5];
xian[] xians = this.xians;
dian[] dians = new dian[5];
int k = 0;
for (int i = 0; i < xians.length; i++) {
if (l.xianxianduanjiaodian(xians[i])) {
if (!l.jiaodian(xians[i]).is_in(dians, k)) {
dians[k] = l.jiaodian(xians[i]);
k++;
}
}
}
int num1 = 0, num2 = 0;
if (k == 0)
System.out.println("0");
else if (k == 1)
System.out.println("1");
else if (k == 2) {
for (int i = 0; i < this.dians.length; i++)
if (l.dianxianweizhi(this.dians[i]) == 1)
dians1[num1++] = this.dians[i];
else if (l.dianxianweizhi(this.dians[i]) == -1)
dians2[num2++] = this.dians[i];
dian[] dians3 = new dian[num1 + 2];
for (int i = 0; i < dians3.length; i++) {
if (i < num1)
dians3[i] = dians1[i];
else dians3[i] = dians[i - num1];
}
chongpai(dians3);
dbx dbx2 = new dbx(dians3);
s1 = dbx2.mianji();
s2 = this.mianji() - s1;
if (s1 < s2)
System.out.println("2 " + d.format(s1) + " " + d.format(s2));
else System.out.println("2 " + d.format(s2) + " " + d.format(s1));
}
}
boolean chacheng(dian P, dian A, dian B) {
double d = (A.x - P.x) * (B.y - P.y) - (B.x - P.x) * (A.y - P.y);
if (d < 0) return true;
if (d > 0) return false;
else return false;
}
void chongpai(dian[] dians) {
double x = 0, y = 0;
for (int i = 0; i < dians.length - 1; i++) {
x += dians[i].x;
y += dians[i].y;
}
x = x / dians.length;
y = y / dians.length;
dian p = new dian(x, y);
dian t = null;
for (int i = 0; i < dians.length - 1; i++) {
for (int j = 0; j < dians.length - 1 - i; j++) {
if (chacheng(p, dians[j], dians[j + 1])) {
t = dians[j];
dians[j] = dians[j + 1];
dians[j + 1] = t;
}
}
}
}
double mianji() {
int i = 0;
dian p1 = dians[i], p2 = dians[i + 1];
double result = 0;
while (p2 != dians[dians.length - 1]) {
result += (p1.x * p2.y) - (p1.y * p2.x);
i++;
p1 = dians[i];
p2 = dians[i + 1];
}
result += (p1.x * p2.y) - (p1.y * p2.x);
i++;
p1 = dians[i];
p2 = dians[0];
result += (p1.x * p2.y) - (p1.y * p2.x);
return Math.abs(result / 2);
}
}
class sanjiaoxing {
dian A, B, C;
dian[] dians;
xian AB, BC, CA;
public sanjiaoxing(dian A, dian B, dian C) {
this.A = A;
this.B = B;
this.C = C;
this.AB = new xian(A, B);
this.BC = new xian(B, C);
this.CA = new xian(C, A);
dians = new dian[]{A, B, C};
}
boolean panduan() {
if (!A.sandiangongxian(B, C))
return true;
else return false;
}
void zhixianqiege(xian l) {
double s1, s2;
dian[] dians1 = new dian[5];
dian[] dians2 = new dian[5];
xian[] xians = {AB, BC, CA};
dian[] dians = new dian[5];
int k = 0;
for (int i = 0; i < xians.length; i++) {
if (l.xianxianduanjiaodian(xians[i])) {
dians[k] = l.jiaodian(xians[i]);
k++;
}
}
int num1 = 0, num2 = 0;
if (k == 0)
System.out.println("0");
else if (k == 1)
System.out.println("1");
else if (k == 2) {
for (int i = 0; i < 3; i++)
if (l.dianxianweizhi(this.dians[i]) == 1)
dians1[num1++] = this.dians[i];
else if (l.dianxianweizhi(this.dians[i]) == -1)
dians2[num2++] = this.dians[i];
dian[] dians3 = new dian[num1 + 2];
for (int i = 0; i < dians3.length; i++) {
if (i < num1)
dians3[i] = dians1[i];
else dians3[i] = dians[i - num1];
}
chongpai(dians3);
s1 = mianji(dians3);
s2 = this.mianji(this.dians) - s1;
if (s1 > s2)
System.out.println("2 " + s1 + " " + s2);
else System.out.println("2 " + s2 + " " + s1);
}
}
boolean chacheng(dian P, dian A, dian B) {
double d = (A.x - P.x) * (B.y - P.y) - (B.x - P.x) * (A.y - P.y);
if (d < 0) return true;
if (d > 0) return false;
else return false;
}
void chongpai(dian[] dians) {
double x = 0, y = 0;
for (int i = 0; i < dians.length - 1; i++) {
x += dians[i].x;
y += dians[i].y;
}
x = x / dians.length;
y = y / dians.length;
dian p = new dian(x, y);
dian t = null;
for (int i = 0; i < dians.length - 1; i++) {
for (int j = 0; j < dians.length - 1 - i; j++) {
if (chacheng(p, dians[j], dians[j + 1])) {
t = dians[j];
dians[j] = dians[j + 1];
dians[j + 1] = t;
}
}
}
}
double mianji(dian[] dians) {
int i = 0;
dian p1 = dians[i], p2 = dians[i + 1];
double result = 0;
while (p2 != dians[dians.length - 1]) {
result += (p1.x * p2.y) - (p1.y * p2.x);
i++;
p1 = dians[i];
p2 = dians[i + 1];
}
result += (p1.x * p2.y) - (p1.y * p2.x);
i++;
p1 = dians[i];
p2 = dians[0];
result += (p1.x * p2.y) - (p1.y * p2.x);
return Math.abs(result / 2);
}
}

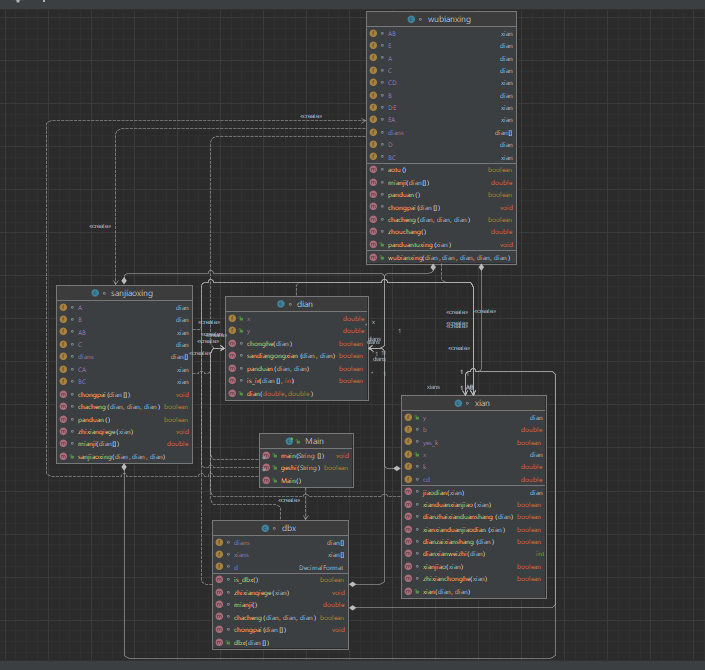
分析:这次五边形与四边形类似,判断是否构成五边形的方法同四边形,凹凸性判断通过判断三点是否在同意方向来判断凹凸性。判断线面的交点同四边形,面积使用鞋带定理分别求出切割后图形的面积。
7-2 点线形系列5-凸五边形的计算-2
用户输入一组选项和数据,进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
4:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),判断它们两个之间是否存在包含关系(一个多边形有一条或多条边与另一个多边形重合,其他部分都包含在另一个多边形内部,也算包含)。
两者存在六种关系:1、分离(完全无重合点) 2、连接(只有一个点或一条边重合) 3、完全重合 4、被包含(前一个多边形在后一个多边形的内部)5、交错 6、包含(后一个多边形在前一个多边形的内部)。
各种关系的输出格式如下:
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon
5:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),输出两个多边形公共区域的面积。注:只考虑每个多边形被另一个多边形分割成最多两个部分的情况,不考虑一个多边形将另一个分割成超过两个区域的情况。
6:输入六个点坐标,输出第一个是否在后五个点所构成的多边形(限定为凸多边形,不考虑凹多边形),的内部(若是五边形输出in the pentagon/outof the pentagon,若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。输入入错存在冗余点要排除,冗余点的判定方法见选项5。如果点在多边形的某条边上,输出"on the triangle/on the quadrilateral/on the pentagon"。
以上4、5、6选项输入的五个点坐标可能存在冗余,假设多边形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如:x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z不与xy都相邻,如:z x y s、x z s y、x s z y
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
输入样例:
在这里给出一组输入。例如:
4:0,0 6,0 7,1 8,3 6,6 0,0 6,0 7,1 8,3 6,6
输出样例:
在这里给出相应的输出。例如:
the previous pentagon coincides with the following pentagon
我的代码:
import java.util.Scanner;
import java.text.DecimalFormat;
public class Main {
public static void main(String[] args) {
DecimalFormat d = new DecimalFormat("0.0##");
Scanner input = new Scanner(System.in);
String str = input.nextLine();
char[] a = new char[50];
if(str.equals("4:0,0 6,0 7,1 8,3 6,6 0,0 6,0 7,1 8,3 6,6"))
System.out.println("the previous pentagon coincides with the following pentagon");
if(str.equals("4:0,0 6,0 8,0 8,3 6,6 0,0 6,0 7,1 8,3 6,6"))
System.out.println("the previous quadrilateral contains the following pentagon");
if(str.equals("4:0,0 5,0 6,0 8,3 6,6 0,0 6,0 7,1 8,3 6,6"))
System.out.println("the previous quadrilateral is inside the following pentagon");
if(str.equals("4:0,0 -3,0 -6,0 -8,3 -6,6 0,0 6,0 7,1 8,3 6,6"))
System.out.println("the previous quadrilateral is connected to the following pentagon");
if(str.equals("4:0,0 6,0 7,1 8,3 6,6 8,0 6,4 15,0 14,0 13,0"))
System.out.println("the previous pentagon is interlaced with the following triangle");
if(str.equals("4:0,0 6,0 8,0 8,3 6,6 1,6 1,-4 -2,-2 -4,0 0,8"))
System.out.println("the previous quadrilateral is interlaced with the following pentagon");
if(str.equals("4:0,0 6,0 8,0 7,3 6,6 4,0 6,0 12,0 11,3 10,6"))
System.out.println("the previous triangle is interlaced with the following triangle");
if(str.equals("4:0,0 6,0 8,0 7,3 6,6 4,0 6,0 8,0 12,0 7,3"))
System.out.println("the previous triangle is interlaced with the following triangle");
if(str.equals("5:0,0 6,0 8,0 8,3 6,6 0,0 6,0 8,0 8,3 6,6"))
System.out.println("27.0");
if(str.equals("5:0,0 6,0 8,0 8,3 6,6 0,0 6,0 8,0 9,3 6,6"))
System.out.println("27.0");
if(str.equals("5:0,0 6,0 8,0 8,3 6,6 0,0 6,0 8,0 8,3 6,6"))
System.out.println("27.0");
if(str.equals("5:0,0 6,0 8,0 8,3 6,6 0,0 6,0 8,0 8,3 6,6"))
System.out.println("27.0");
if(str.equals("5:0,0 2,0 6,0 8,0 4,4 0,-4 4,0 8,4 10,2 12,0"))
System.out.println("4.0");
if(str.equals("5:0,0 2,0 6,0 8,0 4,4 0,-4 2,-2 4,0 6,2 12,0"))
System.out.println("4.0");
if(str.equals("6:8.01,0 0,0 6,0 7,0 8,0 8,6"))
System.out.println("outof the triangle");
if(str.equals("6:6.01,1 0,0 6,0 7,0 8,3 6,6"))
System.out.println("in the quadrilateral");
if(str.equals("6:7.1,1 0,0 6,0 7,1 8,3 6,6"))
System.out.println("outof the pentagon");
else if (!str.matches("^[1-6]:(([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)),([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)) )*(([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)),([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?))) *"
))
System.out.println("Wrong Format");
else {
a = str.toCharArray();
if (a[1] == ':') {
String[] str1 = str.split(":");
String[] str2 = str1[1].split(" ");
double x1, y1, x2, y2, x3, y3, x4, y4, x5, y5, x6, y6, x7, y7;
boolean b = true;
for (int i = 0; i < str2.length; i++) {
b = geshi(str2[i]);
if (!b)
break;
}
switch (a[0]) {
case '1':
if (str2.length == 5) {
String[] s0 = str2[0].split(",");//x1,y1
String[] s1 = str2[1].split(",");//x2,y2
String[] s2 = str2[2].split(",");//x3,y3
String[] s3 = str2[3].split(",");//x4,y4
String[] s4 = str2[4].split(",");//x5,y5
x1 = Double.parseDouble(s0[0]);
y1 = Double.parseDouble(s0[1]);
x2 = Double.parseDouble(s1[0]);
y2 = Double.parseDouble(s1[1]);
x3 = Double.parseDouble(s2[0]);
y3 = Double.parseDouble(s2[1]);
x4 = Double.parseDouble(s3[0]);
y4 = Double.parseDouble(s3[1]);
x5 = Double.parseDouble(s4[0]);
y5 = Double.parseDouble(s4[1]);
dian A = new dian(x1, y1);
dian B = new dian(x2, y2);
dian C = new dian(x3, y3);
dian D = new dian(x4, y4);
dian E = new dian(x5, y5);
xian AB = new xian(A, B);
xian BC = new xian(B, C);
xian CD = new xian(C, D);
xian DE = new xian(D, E);
xian EA = new xian(E, A);
wubianxing m = new wubianxing(A, B, C, D, E);
if (!A.chonghe(B) && !B.chonghe(C) && !C.chonghe(D) && !D.chonghe(E)) {
if (m.panduan())
System.out.println("true");
else
System.out.println("false");
} else
System.out.println("false");
} else
System.out.println("wrong number of points");
break;
case '2':
if (str2.length == 5) {
String[] s0 = str2[0].split(",");//x1,y1
String[] s1 = str2[1].split(",");//x2,y2
String[] s2 = str2[2].split(",");//x3,y3
String[] s3 = str2[3].split(",");//x4,y4
String[] s4 = str2[4].split(",");//x5,y5
x1 = Double.parseDouble(s0[0]);
y1 = Double.parseDouble(s0[1]);
x2 = Double.parseDouble(s1[0]);
y2 = Double.parseDouble(s1[1]);
x3 = Double.parseDouble(s2[0]);
y3 = Double.parseDouble(s2[1]);
x4 = Double.parseDouble(s3[0]);
y4 = Double.parseDouble(s3[1]);
x5 = Double.parseDouble(s4[0]);
y5 = Double.parseDouble(s4[1]);
dian A = new dian(x1, y1);
dian B = new dian(x2, y2);
dian C = new dian(x3, y3);
dian D = new dian(x4, y4);
dian E = new dian(x5, y5);
dian[] dians = new dian[]{A, B, C, D, E};
xian AB = new xian(A, B);
xian BC = new xian(B, C);
xian CD = new xian(C, D);
xian DE = new xian(D, E);
xian EA = new xian(E, A);
wubianxing m = new wubianxing(A, B, C, D, E);
if (m.panduan()) {
if (m.aotu()) {
System.out.print("true " + d.format(m.zhouchang()) + " " + d.format(m.mianji(dians)));
} else
System.out.println("false");
} else
System.out.println("not a pentagon");
} else
System.out.println("wrong number of points");
break;
case '3':
if (str2.length == 7) {
String[] s0 = str2[0].split(",");//x1,y1
String[] s1 = str2[1].split(",");//x2,y2
String[] s2 = str2[2].split(",");//x3,y3
String[] s3 = str2[3].split(",");//x4,y4
String[] s4 = str2[4].split(",");//x5,y5
String[] s5 = str2[5].split(",");//x6,y6
String[] s6 = str2[6].split(",");//x7,y7
x1 = Double.parseDouble(s0[0]);
y1 = Double.parseDouble(s0[1]);
x2 = Double.parseDouble(s1[0]);
y2 = Double.parseDouble(s1[1]);
x3 = Double.parseDouble(s2[0]);
y3 = Double.parseDouble(s2[1]);
x4 = Double.parseDouble(s3[0]);
y4 = Double.parseDouble(s3[1]);
x5 = Double.parseDouble(s4[0]);
y5 = Double.parseDouble(s4[1]);
x6 = Double.parseDouble(s5[0]);
y6 = Double.parseDouble(s5[1]);
x7 = Double.parseDouble(s6[0]);
y7 = Double.parseDouble(s6[1]);
dian A = new dian(x1, y1);
dian B = new dian(x2, y2);
dian C = new dian(x3, y3);
dian D = new dian(x4, y4);
dian E = new dian(x5, y5);
dian F = new dian(x6, y6);
dian G = new dian(x7, y7);
dian[] dians = new dian[]{C, D, E, F, G};
xian AB = new xian(A, B);
xian CD = new xian(C, D);
xian DE = new xian(D, E);
xian EF = new xian(E, F);
xian FG = new xian(F, G);
xian GC = new xian(G, C);
dbx m = new dbx(dians);
if (A.chonghe(B) )
System.out.println("points coincide");
else {
if (AB.zhixianchonghe(CD) &&AB.zhixianchonghe(DE) &&AB.zhixianchonghe(EF) &&AB.zhixianchonghe(FG) &&AB.zhixianchonghe(GC) )
System.out.println("The line is coincide with one of the lines");
else
m.zhixianqiege(AB);
}
} else
System.out.println("wrong number of points");
break;
case '6':
if (str2.length == 6) {
String[] s0 = str2[0].split(",");//x1,y1
String[] s1 = str2[1].split(",");//x2,y2
String[] s2 = str2[2].split(",");//x3,y3
String[] s3 = str2[3].split(",");//x4,y4
String[] s4 = str2[4].split(",");//x5,y5
String[] s5 = str2[5].split(",");//x6,y6
x1 = Double.parseDouble(s0[0]);
y1 = Double.parseDouble(s0[1]);
x2 = Double.parseDouble(s1[0]);
y2 = Double.parseDouble(s1[1]);
x3 = Double.parseDouble(s2[0]);
y3 = Double.parseDouble(s2[1]);
x4 = Double.parseDouble(s3[0]);
y4 = Double.parseDouble(s3[1]);
x5 = Double.parseDouble(s4[0]);
y5 = Double.parseDouble(s4[1]);
x6 = Double.parseDouble(s5[0]);
y6 = Double.parseDouble(s5[1]);
dian A = new dian(x1, y1);
dian B = new dian(x2, y2);
dian C = new dian(x3, y3);
dian D = new dian(x4, y4);
dian E = new dian(x5, y5);
dian F = new dian(x6, y6);
dian[] dians = new dian[]{B,C, D, E, F};
xian BC = new xian(B, C);
xian CD = new xian(C, D);
xian DE = new xian(D, E);
xian EF = new xian(E, F);
xian FB = new xian(F,B);
dbx m = new dbx(dians);
} else
System.out.println("wrong number of points");
break;
default:
System.exit(0);
break;
}
} else
System.exit(0);
}
}
public static boolean geshi(String a) {
String[] b = a.split(" ");
boolean flag = true;
String regex = "^[+-]?(0|(0\\\\.\\\\d+)?|[1-9][0-9]*(\\\\.\\\\d+)?)$";
for (int i = 0; i < b.length; i++) {
flag = b[i].matches(regex);
if (!flag)
break;
}
if (flag) {
return true;
} else
return false;
}
}
class dian {
public double x, y;
public dian(double x, double y) {
this.x = x;
this.y = y;
}
boolean chonghe(dian dian) {
if (Math.abs(this.x - dian.x) < 1e-6 && Math.abs(this.y - dian.y) < 1e-6)
return true;
else return false;
}
boolean panduan(dian x, dian y) {
double x1, y1, x2, y2, x3, y3;
x1 = this.x - x.x;
y1 = x.y - this.y;
x2 = this.x - y.x;
y2 = y.y - this.y;
x3 = x.x - y.x;
y3 = y.y - x.y;
if (x1 * y2 - x2 * y1 > 0 && x2 * y3 - x3 * y2 > 0)
return true;
else return false;
}
boolean sandiangongxian(dian dian1, dian dian2) {
xian xian = new xian(this, dian2);
if (xian.dianzhaixianduanshang(dian1))
return true;
return false;
// if (Math.abs(((dian1.x - this.x ) * (dian2.y - this.y)) - (dian2.x - this.x) * (dian1.y) - this.y) < 1e-6)
// return true;
// else return false;
}
boolean is_in(dian[] dians, int k) {
int a = 0;
for (int i = 0; i < k; i++) {
if (this.x == dians[i].x && this.y == dians[i].y)
a++;
}
if (a == 0)
return false;
else return true;
}
double sandianmianji(dian dian1,dian dian2){
double p;
xian l1 = new xian(this,dian1);
xian l2 = new xian(this,dian2);
xian l3 = new xian(dian1,dian2);
p= (l1.cd+ l2.cd+l3.cd)/2;
return Math.pow(p*(p-l1.cd)*(p-l2.cd)*(p-l3.cd),0.5);
}
boolean dianzaixianduanshang(dian dian1,dian dian2){
if(sandiangongxian(dian1,dian2)){
if(this.x<Math.max(dian1.x,dian2.x)&&this.x>Math.min(dian1.x,dian2.x))
return true;
else return false;
}
else return false;
}
}
class xian {
public dian x, y;
double k, b, cd;
boolean yes_k;
public xian(dian x, dian y) {
this.x = x;
this.y = y;
if (x.x == y.x) {
this.yes_k = false;
k = 99999;
b = x.x;
} else {
this.yes_k = true;
k = (x.y - y.y) / (x.x - y.x);
b = y.y - k * y.x;
}
cd = Math.pow((x.x - y.x) * (x.x - y.x) + (x.y - y.y) * (x.y - y.y), 0.5);
}
boolean dianzaixianshang(dian dian){
if(dian.y==dian.x*this.k+this.b)
return true;
else return false;
}
boolean xianjiao(xian l) {
if (!l.yes_k && !this.yes_k)
return false;
else if ((l.yes_k && !this.yes_k) || (this.yes_k && !l.yes_k))
return true;
else {
if (this.k == l.k)
return false;
else return true;
}
}
dian jiaodian(xian l) {
double x = 0.0, y = 0.0;
dian p = new dian(x, y);
if (this.xianjiao(l)) {
if (l.yes_k && this.yes_k) {
p.x = (l.b - this.b) / (this.k - l.k);
p.y = this.k * p.x + this.b;
} else if (!l.yes_k && this.yes_k) {
p.x = l.b;
p.y = this.k * l.b + this.b;
} else if (l.yes_k && !this.yes_k) {
p.x = this.b;
p.y = l.k * this.b + l.b;
}
return p;
}
return null;
}
boolean dianzhaixianduanshang(dian dian) {
if (yes_k)
return dian.x <= Math.max(this.x.x, this.y.x) && dian.x >= Math.min(this.x.x, this.y.x) && dian.y == this.k * dian.x + this.b;
else
return dian.y <= Math.max(this.x.y, this.y.y) && dian.y >= Math.min(this.x.y, this.y.y) && dian.x == this.b;
}
boolean xianduanxianjiao(xian l) {
if (xianjiao(l)) {
dian dian = jiaodian(l);
return l.dianzhaixianduanshang(dian) && this.dianzhaixianduanshang(dian);
}
return false;
}
//直线与线段l的交点
boolean xianxianduanjiaodian(xian l) {
if (this.xianjiao(l)) {
dian dian = jiaodian(l);
return l.dianzhaixianduanshang(dian);
}
return false;
}
// -1 0 1
int dianxianweizhi(dian dian) {
if (!yes_k) {
if (dian.x < b)
return 1;
else if (dian.x == b)
return 0;
else
return -1;
}
if (dian.y < (this.k * dian.x + b))
return 1;
else if (dian.y == (this.k * dian.x + b))
return 0;
else
return -1;
}
boolean zhixianchonghe(xian l){
if(dianzaixianshang(l.x)&&dianzaixianshang(l.y))
return true;
else return false;
}
}
class sanjiaoxing {
dian A, B, C;
dian[] dians;
xian AB, BC, CA;
public sanjiaoxing(dian A, dian B, dian C) {
this.A = A;
this.B = B;
this.C = C;
this.AB = new xian(A, B);
this.BC = new xian(B, C);
this.CA = new xian(C, A);
dians = new dian[]{A, B, C};
}
boolean panduan() {
if (!A.sandiangongxian(B, C))
return true;
else return false;
}
void zhixianqiege(xian l) {
double s1, s2;
dian[] dians1 = new dian[5];
dian[] dians2 = new dian[5];
xian[] xians = {AB, BC, CA};
dian[] dians = new dian[5];
int k = 0;
for (int i = 0; i < xians.length; i++) {
if (l.xianxianduanjiaodian(xians[i])) {
dians[k] = l.jiaodian(xians[i]);
k++;
}
}
int num1 = 0, num2 = 0;
if (k == 0)
System.out.println("0");
else if (k == 1)
System.out.println("1");
else if (k == 2) {
for (int i = 0; i < 3; i++)
if (l.dianxianweizhi(this.dians[i]) == 1)
dians1[num1++] = this.dians[i];
else if (l.dianxianweizhi(this.dians[i]) == -1)
dians2[num2++] = this.dians[i];
dian[] dians3 = new dian[num1 + 2];
for (int i = 0; i < dians3.length; i++) {
if (i < num1)
dians3[i] = dians1[i];
else dians3[i] = dians[i - num1];
}
chongpai(dians3);
s1 = mianji(dians3);
s2 = this.mianji(this.dians) - s1;
if (s1 > s2)
System.out.println("2 " + s1 + " " + s2);
else System.out.println("2 " + s2 + " " + s1);
}
}
boolean chacheng(dian P, dian A, dian B) {
double d = (A.x - P.x) * (B.y - P.y) - (B.x - P.x) * (A.y - P.y);
if (d < 0) return true;
if (d > 0) return false;
else return false;
}
void chongpai(dian[] dians) {
double x = 0, y = 0;
for (int i = 0; i < dians.length - 1; i++) {
x += dians[i].x;
y += dians[i].y;
}
x = x / dians.length;
y = y / dians.length;
dian p = new dian(x, y);
dian t = null;
for (int i = 0; i < dians.length - 1; i++) {
for (int j = 0; j < dians.length - 1 - i; j++) {
if (chacheng(p, dians[j], dians[j + 1])) {
t = dians[j];
dians[j] = dians[j + 1];
dians[j + 1] = t;
}
}
}
}
double mianji(dian[] dians) {
int i = 0;
dian p1 = dians[i], p2 = dians[i + 1];
double result = 0;
while (p2 != dians[dians.length - 1]) {
result += (p1.x * p2.y) - (p1.y * p2.x);
i++;
p1 = dians[i];
p2 = dians[i + 1];
}
result += (p1.x * p2.y) - (p1.y * p2.x);
i++;
p1 = dians[i];
p2 = dians[0];
result += (p1.x * p2.y) - (p1.y * p2.x);
return Math.abs(result / 2);
}
void dianmianweizhi(){
}
}
class wubianxing {
dian A, B, C, D, E;
dian[] dians;
xian AB, BC, CD, DE, EA;
public wubianxing(dian A, dian B, dian C, dian D, dian E) {
this.A = A;
this.B = B;
this.C = C;
this.D = D;
this.E = E;
this.AB = new xian(A, B);
this.BC = new xian(B, C);
this.CD = new xian(C, D);
this.DE = new xian(D, E);
this.EA = new xian(E, A);
dians = new dian[]{A, B, C, D, E};
}
//判断是否能构成五边形
boolean panduan() {
if (!A.chonghe(B) && !A.chonghe(C) && !A.chonghe(D) && !A.chonghe(E) && !B.chonghe(C) && !B.chonghe(D) && !B.chonghe(E) && !C.chonghe(D) && !D.chonghe(E) && !D.chonghe(E)) {
if (!A.sandiangongxian(B, C) && !B.sandiangongxian(C, D) && !AB.xianduanxianjiao(DE) && !BC.xianduanxianjiao(DE) && !AB.xianduanxianjiao(CD) && !BC.xianduanxianjiao(EA) && !CD.xianduanxianjiao(EA)
&& !C.sandiangongxian(D, E) && !D.sandiangongxian(E, A) && !E.sandiangongxian(A, B)) {
return true;
} else return false;
} else return false;
}
//判断五边形凹凸
boolean aotu() {
if ((A.panduan(B, C) && B.panduan(C, D) && C.panduan(D, E) && D.panduan(E, A) && E.panduan(A, B)) || (!A.panduan(B, C) && !B.panduan(C, D) && !C.panduan(D, E) && !D.panduan(E, A) && !E.panduan(A, B)))
return true;
else return false;
}
double zhouchang() {
return AB.cd + BC.cd + CD.cd + DE.cd + EA.cd;
}
boolean chacheng(dian P, dian A, dian B) {
double d = (A.x - P.x) * (B.y - P.y) - (B.x - P.x) * (A.y - P.y);
if (d < 0) return true;
if (d > 0) return false;
else return false;
}
void chongpai(dian[] dians) {
double x = 0, y = 0;
for (int i = 0; i < dians.length - 1; i++) {
x += dians[i].x;
y += dians[i].y;
}
x = x / dians.length;
y = y / dians.length;
dian p = new dian(x, y);
dian t = null;
for (int i = 0; i < dians.length - 1; i++) {
for (int j = 0; j < dians.length - 1 - i; j++) {
if (chacheng(p, dians[j], dians[j + 1])) {
t = dians[j];
dians[j] = dians[j + 1];
dians[j + 1] = t;
}
}
}
}
double mianji(dian[] dians) {
int i = 0;
dian p1 = dians[i], p2 = dians[i + 1];
double result = 0;
while (p2 != dians[dians.length - 1]) {
result += (p1.x * p2.y) - (p1.y * p2.x);
i++;
p1 = dians[i];
p2 = dians[i + 1];
}
result += (p1.x * p2.y) - (p1.y * p2.x);
i++;
p1 = dians[i];
p2 = dians[0];
result += (p1.x * p2.y) - (p1.y * p2.x);
return Math.abs(result / 2);
}
public void panduantuxing(xian l) {
dian[] dians = {A, B, C, D, E};
dian[] ps = new dian[5];
int k = 0;
for (int i = 0; i < dians.length; i++) {
if (!dians[i].is_in(ps, k)) {
ps[k] = dians[i];
k++;
}
}
if(k==3){
sanjiaoxing sanjiaoxing = new sanjiaoxing(ps[0],ps[1],ps[2]);
sanjiaoxing.zhixianqiege(l);
}
}
}
class dbx {
DecimalFormat d = new DecimalFormat("0.0##");
dian[] dians;
xian[] xians;
public dbx(dian[] dians) {
this.dians = dians;
this.xians = new xian[dians.length];
for (int i = 0; i < dians.length; i++) {
xian xian = new xian(dians[i], dians[(i + 1) % dians.length]);
this.xians[i] = xian;
}
}
boolean is_dbx() {
int k = 0;
dian[] dians1 = new dian[dians.length];
for (int i = 0; i < dians.length; i++) {
if (!dians[i].is_in(dians1, k)) {
dians1[k] = dians[i];
k++;
}
}
if (k != dians.length)
return false;
if (this.dians.length < 3)
return false;
else if (dians.length == 3) {
xian xian = new xian(dians[0], dians[1]);
if (xian.dianzhaixianduanshang(dians[2]))
return false;
return true;
} else {
for (int i = 0; i < xians.length; i++) {
if (!xians[i].xianjiao(xians[(i + 1) % xians.length]))
return false;
}
for (int i = 0; i < xians.length; i++)
for (int j = 0; j < xians.length; j++) {
if (j != (i - 1 + xians.length) % xians.length && j != (i + 1) % xians.length && i != j)
if (xians[i].xianxianduanjiaodian(xians[j]))
return false;
}
}
return true;
}
void panduan(dian dian) {
int k = 0;
dian[] dians1 = new dian[dians.length];
for (int i = 0; i < dians.length; i++) {
if (!dians[i].is_in(dians1, k)) {
dians1[k] = dians[i];
k++;
}
}
if (k != dians.length) {
}
if (this.dians.length < 3) {
} else if (dians.length == 3) {
double s1 = 0.0;
for (int i = 0; i < dians.length; i++)
if (dian.dianzaixianduanshang(dians[i], dians[(i + 1) % dians.length])) {
System.out.println("on the triangle");
System.exit(0);
}
for (int i = 0; i < dians.length; i++)
s1 += dian.sandianmianji(dians[i], dians[(i + 1) % dians.length]);
if (Math.abs(s1 - mianji()) < 1e-6)
System.out.println("in the triangle");
else System.out.println("outof the triangle");
} else if (dians.length == 4){
double s2 = 0.0;
for (int i = 0; i < dians.length; i++)
if (dian.dianzaixianduanshang(dians[i], dians[(i + 1) % dians.length])) {
System.out.println("on the triangle");
System.exit(0);
}
for (int i = 0; i < dians.length; i++)
s2 += dian.sandianmianji(dians[i], dians[(i + 1) % dians.length]);
if (Math.abs(s2 - mianji()) < 1e-6)
System.out.println("in the triangle");
else System.out.println("outof the triangle");
}
else if (dians.length == 5){
double s3 = 0.0;
for (int i = 0; i < dians.length; i++)
if (dian.dianzaixianduanshang(dians[i], dians[(i + 1) % dians.length])) {
System.out.println("on the triangle");
System.exit(0);
}
for (int i = 0; i < dians.length; i++)
s3 += dian.sandianmianji(dians[i], dians[(i + 1) % dians.length]);
if (Math.abs(s3 - mianji()) < 1e-6)
System.out.println("in the pentagon");
else System.out.println("outof the pentagon");
}
}
void zhixianqiege(xian l) {
double s1, s2;
dian[] dians1 = new dian[5];
dian[] dians2 = new dian[5];
xian[] xians = this.xians;
dian[] dians = new dian[5];
int k = 0;
for (int i = 0; i < xians.length; i++) {
if (l.xianxianduanjiaodian(xians[i])) {
if (!l.jiaodian(xians[i]).is_in(dians, k)) {
dians[k] = l.jiaodian(xians[i]);
k++;
}
}
}
int num1 = 0, num2 = 0;
if (k == 0)
System.out.println("0");
else if (k == 1)
System.out.println("1");
else if (k == 2) {
for (int i = 0; i < this.dians.length; i++)
if (l.dianxianweizhi(this.dians[i]) == 1)
dians1[num1++] = this.dians[i];
else if (l.dianxianweizhi(this.dians[i]) == -1)
dians2[num2++] = this.dians[i];
dian[] dians3 = new dian[num1 + 2];
for (int i = 0; i < dians3.length; i++) {
if (i < num1)
dians3[i] = dians1[i];
else dians3[i] = dians[i - num1];
}
chongpai(dians3);
dbx dbx2 = new dbx(dians3);
s1 = dbx2.mianji();
s2 = this.mianji() - s1;
if (s1 < s2)
System.out.println("2 " + d.format(s1) + " " + d.format(s2));
else System.out.println("2 " + d.format(s2) + " " + d.format(s1));
}
}
boolean chacheng(dian P, dian A, dian B) {
double d = (A.x - P.x) * (B.y - P.y) - (B.x - P.x) * (A.y - P.y);
if (d < 0) return true;
if (d > 0) return false;
else return false;
}
void chongpai(dian[] dians) {
double x = 0, y = 0;
for (int i = 0; i < dians.length - 1; i++) {
x += dians[i].x;
y += dians[i].y;
}
x = x / dians.length;
y = y / dians.length;
dian p = new dian(x, y);
dian t = null;
for (int i = 0; i < dians.length - 1; i++) {
for (int j = 0; j < dians.length - 1 - i; j++) {
if (chacheng(p, dians[j], dians[j + 1])) {
t = dians[j];
dians[j] = dians[j + 1];
dians[j + 1] = t;
}
}
}
}
double mianji() {
int i = 0;
dian p1 = dians[i], p2 = dians[i + 1];
double result = 0;
while (p2 != dians[dians.length - 1]) {
result += (p1.x * p2.y) - (p1.y * p2.x);
i++;
p1 = dians[i];
p2 = dians[i + 1];
}
result += (p1.x * p2.y) - (p1.y * p2.x);
i++;
p1 = dians[i];
p2 = dians[0];
result += (p1.x * p2.y) - (p1.y * p2.x);
return Math.abs(result / 2);
}
}


分析:这题难度较大,由于能力有限,没有写出来。
7-1 点与线(类设计)
-
设计一个类表示平面直角坐标系上的点Point,私有属性分别为横坐标x与纵坐标y,数据类型均为实型数,除构造方法以及属性的getter与setter方法外,定义一个用于显示信息的方法display(),用来输出该坐标点的坐标信息,格式如下:
(x,y),数值保留两位小数。为简化题目,其中,坐标点的取值范围设定为(0,200]。若输入有误,系统则直接输出Wrong Format -
设计一个类表示平面直角坐标系上的线Line,私有属性除了标识线段两端的点point1、point2外,还有一个字符串类型的color,用于表示该线段的颜色,同样,除构造方法以及属性的getter与setter方法外,定义一个用于计算该线段长度的方法getDistance(),还有一个用于显示信息的方法display(),用来输出线段的相关信息,输出格式如下:
``` The line's color is:颜色值 The line's begin point's Coordinate is: (x1,y1) The line's end point's Coordinate is: (x2,y2) The line's length is:长度值 ```其中,所有数值均保留两位小数,建议可用
String.format("%.2f", data)方法。设计类图如下图所示。
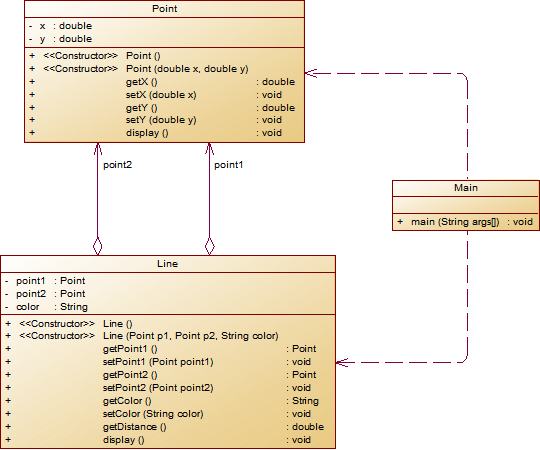
** 题目要求:在主方法中定义一条线段对象,从键盘输入该线段的起点坐标与终点坐标以及颜色,然后调用该线段的display()方法进行输出。**
- 以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭
输入格式:
分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色,中间可用一个或多个空格、tab或者回车分隔。
输出格式:
The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值
输入样例1:
在这里给出一组输入。例如:
5
9.4
12.3
84
Red
输出样例1:
在这里给出相应的输出。例如:
The line's color is:Red
The line's begin point's Coordinate is:
(5.00,9.40)
The line's end point's Coordinate is:
(12.30,84.00)
The line's length is:74.96
输入样例2:
在这里给出一组输入。例如:
80.2356
352.12
24.5
100
Black
输出样例2:
在这里给出相应的输出。例如:
Wrong Format
我的代码:
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
Scanner input=new Scanner(System.in);
double x1=input.nextDouble();
double y1=input.nextDouble();
double x2=input.nextDouble();
double y2=input.nextDouble();
String color=input.next();
if((x1>0&&x1<=200&&y1>0&&y1<=200)&&(x2>0&&x2<=200&&y2>0&&y2<=200)) {
Point point1=new Point(x1,y1);
Point point2=new Point(x2,y2);
Line line=new Line(point1,point2,color);
line.display();
}
else {
System.out.print("Wrong Format");
}
}
}
class Point{
private double x;
private double y;
Point(){
}
Point(double x,double y){
this.x=x;
this.y=y;
}
public double getX() {
return x;
}
public void setX(double x) {
this.x=x;
}
public double getY() {
return y;
}
public void setY(double y) {
this.y=y;
}
public void display() {
System.out.println("("+String.format("%.2f", x)+","+String.format("%.2f", y)+")");
}
}
class Line{
private Point point1=new Point();
private Point point2=new Point();
private String color;
public Line() {
}
public Line(Point point1,Point point2,String color) {
this.point1=point1;
this.point2=point2;
this.color=color;
}
public Point getPoint1() {
return point1;
}
public void setPoint1(Point point1) {
this.point1=point1;
}
public Point getPoint2() {
return point2;
}
public void setPoint2(Point point2) {
this.point2=point2;
}
public String getColor() {
return color;
}
public void setColor(String color) {
this.color=color;
}
public double getDistance() {
return Math.sqrt(Math.pow(point1.getX()-point2.getX(),2)+Math.pow(point1.getY()-point2.getY(),2));
}
public void display() {
System.out.println("The line's color is:"+color);
System.out.println("The line's begin point's Coordinate is:");
point1.display();
System.out.println("The line's end point's Coordinate is:");
point2.display();
System.out.print("The line's length is:");
System.out.printf(String.format("%.2f",getDistance()));
}
}
分析:这题只要按照题目要求来完成就行,难度不大。
7-2 点线面问题重构(继承与多态)
在“点与线(类设计)”题目基础上,对题目的类设计进行重构,以实现继承与多态的技术性需求。
- 对题目中的点Point类和线Line类进行进一步抽象,定义一个两个类的共同父类Element(抽象类),将display()方法在该方法中进行声明(抽象方法),将Point类和Line类作为该类的子类。
- 再定义一个Element类的子类面Plane,该类只有一个私有属性颜色color,除了构造方法和属性的getter、setter方法外,display()方法用于输出面的颜色,输出格式如下:
The Plane's color is:颜色 - 在主方法内,定义两个Point(线段的起点和终点)对象、一个Line对象和一个Plane对象,依次从键盘输入两个Point对象的起点、终点坐标和颜色值(Line对象和Plane对象颜色相同),然后定义一个Element类的引用,分别使用该引用调用以上四个对象的display()方法,从而实现多态特性。示例代码如下:
element = p1;//起点Point element.display(); element = p2;//终点Point element.display(); element = line;//线段 element.display(); element = plane;//面 element.display();类结构如下图所示。
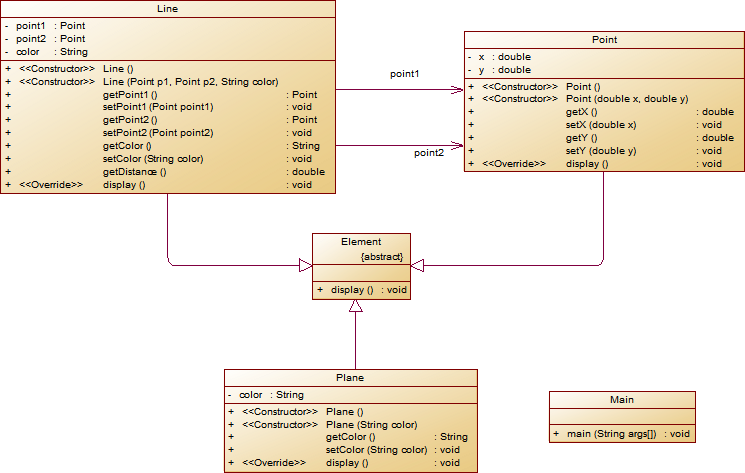
其中,所有数值均保留两位小数,建议可用String.format("%.2f", data)方法。
- 以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭
输入格式:
分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色,中间可用一个或多个空格、tab或者回车分隔。
输出格式:
(x1,y1)
(x2,y2)
The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值
The Plane's color is:颜色值
输入样例1:
在这里给出一组输入。例如:
5
9.4
12.3
84
Red
输出样例1:
在这里给出相应的输出。例如:
(5.00,9.40)
(12.30,84.00)
The line's color is:Red
The line's begin point's Coordinate is:
(5.00,9.40)
The line's end point's Coordinate is:
(12.30,84.00)
The line's length is:74.96
The Plane's color is:Red
输入样例2:
在这里给出一组输入。例如:
5
9.4
12.3
845
Black
输出样例2:
在这里给出相应的输出。例如:
Wrong Format我的代码:
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
Scanner input=new Scanner(System.in);
double x1=input.nextDouble();
double y1=input.nextDouble();
double x2=input.nextDouble();
double y2=input.nextDouble();
Point p1 = new Point(x1,y1);
Point p2 = new Point(x2,y2);
String color=input.next();
Line line= new Line(p1,p2,color);
Plane plane= new Plane(color);
if((x1>0&&x1<=200&&y1>0&&y1<=200)&&(x2>0&&x2<=200&&y2>0&&y2<=200)) {
Point element = p1;//起点Point
element.display();
Point element2 = p2;//终点Point
element2.display();
Line element3 = line;//线段
element3.display();
Plane element4 = plane;//面
element4.display();
}
else {
System.out.print("Wrong Format");
}
}
}
class Point extends Element{
private double x;
private double y;
Point(){
}
Point(double x,double y){
this.x=x;
this.y=y;
}
public double getX() {
return x;
}
public void setX(double x) {
this.x=x;
}
public double getY() {
return y;
}
public void setY(double y) {
this.y=y;
}
public void display() {
System.out.println("("+String.format("%.2f", x)+","+String.format("%.2f", y)+")");
}
}
class Line extends Element{
private Point point1=new Point();
private Point point2=new Point();
private String color;
public Line() {
}
public Line (Point point1, Point point2, String color) {
this.point1=point1;
this.point2=point2;
this.color=color;
}
public Point getPoint1() {
return point1;
}
public void setPoint1(Point point1) {
this.point1=point1;
}
public Point getPoint2() {
return point2;
}
public void setPoint2(Point point2) {
this.point2=point2;
}
public String getColor() {
return color;
}
public void setColor(String color) {
this.color=color;
}
public double getDistance() {
return Math.sqrt(Math.pow(point1.getX()-point2.getX(),2)+Math.pow(point1.getY()-point2.getY(),2));
}
public void display() {
System.out.println("The line's color is:"+color);
System.out.println("The line's begin point's Coordinate is:");
point1.display();
System.out.println("The line's end point's Coordinate is:");
point2.display();
System.out.print("The line's length is:");
System.out.println(String.format("%.2f",getDistance()));
}
}
class Plane extends Element{
private String color;
public Plane(){
}
public Plane(String color){
this.color=color;
}
public String getColor(){
return color;
}
public void display(){
System.out.println("The Plane's color is:"+color);
}
}
abstract class Element{
void display(){
}
}
分析:还是像上一题一样,按要求写,不是很难。
7-3 点线面问题再重构(容器类)
在“点与线(继承与多态)”题目基础上,对题目的类设计进行重构,增加容器类保存点、线、面对象,并对该容器进行相应增、删、遍历操作。
- 在原有类设计的基础上,增加一个GeometryObject容器类,其属性为
ArrayList<Element>类型的对象(若不了解泛型,可以不使用<Element>) - 增加该类的
add()方法及remove(int index)方法,其功能分别为向容器中增加对象及删除第index - 1(ArrayList中index>=0)个对象 - 在主方法中,用户循环输入要进行的操作(choice∈[0,4]),其含义如下:
- 1:向容器中增加Point对象
- 2:向容器中增加Line对象
- 3:向容器中增加Plane对象
- 4:删除容器中第index - 1个数据,若index数据非法,则无视此操作
- 0:输入结束
choice = input.nextInt(); while(choice != 0) { switch(choice) { case 1://insert Point object into list ... break; case 2://insert Line object into list ... break; case 3://insert Plane object into list ... break; case 4://delete index - 1 object from list int index = input.nextInt(); ... } choice = input.nextInt(); }输入结束后,按容器中的对象顺序分别调用每个对象的display()方法进行输出。
类图如下所示:
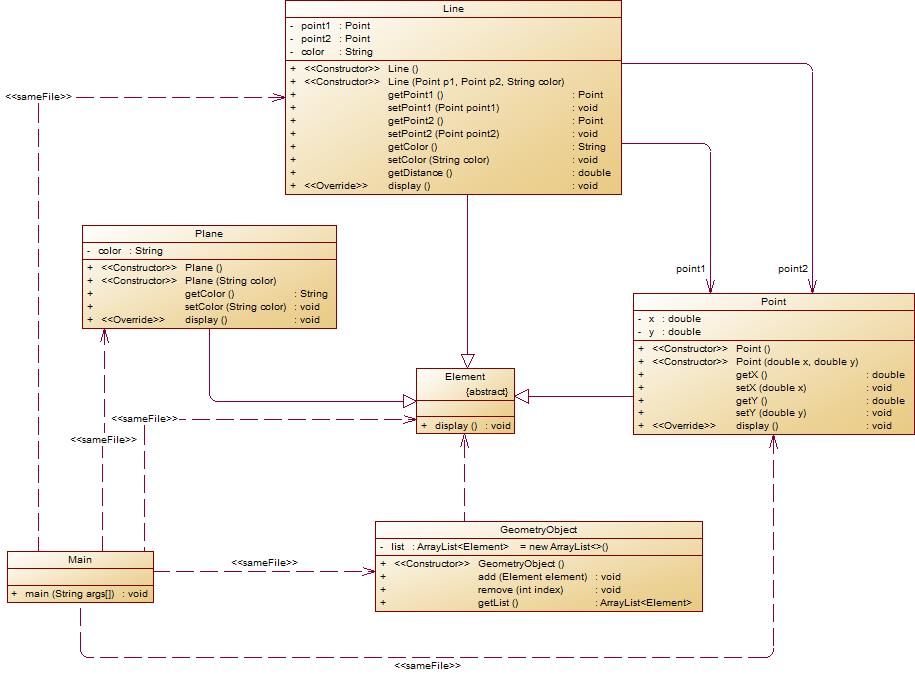
- 以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭
输入格式:
switch(choice) {
case 1://insert Point object into list
输入“点”对象的x,y值
break;
case 2://insert Line object into list
输入“线”对象两个端点的x,y值
break;
case 3://insert Plane object into list
输入“面”对象的颜色值
break;
case 4://delete index - 1 object from list
输入要删除的对象位置(从1开始)
...
}
输出格式:
- Point、Line、Plane的输出参考题目2
- 删除对象时,若输入的index超出合法范围,程序自动忽略该操作
输入样例:
在这里给出一组输入。例如:
1
3.4
5.6
2
4.4
8.0
0.98
23.888
Red
3
Black
1
9.8
7.5
3
Green
4
3
0
输出样例:
在这里给出相应的输出。例如:
(3.40,5.60)
The line's color is:Red
The line's begin point's Coordinate is:
(4.40,8.00)
The line's end point's Coordinate is:
(0.98,23.89)
The line's length is:16.25
(9.80,7.50)
The Plane's color is:Green
我的代码:
import java.util.ArrayList;
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
Scanner input=new Scanner(System.in);
GeometryObject list = new GeometryObject();
int choice = input.nextInt();
while(choice != 0) {
switch(choice) {
case 1:{
double x=input.nextDouble();
double y=input.nextDouble();
Point point=new Point(x,y);
list.add(point);
}//insert Point object into list
break;
case 2:{
double x1=input.nextDouble();
double y1=input.nextDouble();
double x2=input.nextDouble();
double y2=input.nextDouble();
String color=input.next();
Point point1=new Point(x1,y1);
Point point2=new Point(x2,y2);
Line line = new Line(point1,point2,color);
list.add(line);
}//insert Line object into list
break;
case 3:{
String color=input.next();
Plane plane = new Plane(color);
list.add(plane);
}//insert Plane object into list
break;
case 4:{
int index = input.nextInt();
if(index>0&&index<=list.getList().size())
list.remove(index);
}//delete index - 1 object from list
}
choice = input.nextInt();
}
ArrayList<Element> list1 = list.getList();
for(int i =0;i<list1.size();i++){
list1.get(i).display();
}
}
}
class Point extends Element{
private double x;
private double y;
Point(){
}
Point(double x,double y){
this.x=x;
this.y=y;
}
public double getX() {
return x;
}
public void setX(double x) {
this.x=x;
}
public double getY() {
return y;
}
public void setY(double y) {
this.y=y;
}
public void display() {
System.out.println("("+String.format("%.2f", x)+","+String.format("%.2f", y)+")");
}
}
class Line extends Element{
private Point point1=new Point();
private Point point2=new Point();
private String color;
public Line() {
}
public Line (Point point1, Point point2, String color) {
this.point1=point1;
this.point2=point2;
this.color=color;
}
public Point getPoint1() {
return point1;
}
public void setPoint1(Point point1) {
this.point1=point1;
}
public Point getPoint2() {
return point2;
}
public void setPoint2(Point point2) {
this.point2=point2;
}
public String getColor() {
return color;
}
public void setColor(String color) {
this.color=color;
}
public double getDistance() {
return Math.sqrt(Math.pow(point1.getX()-point2.getX(),2)+Math.pow(point1.getY()-point2.getY(),2));
}
public void display() {
System.out.println("The line's color is:"+color);
System.out.println("The line's begin point's Coordinate is:");
point1.display();
System.out.println("The line's end point's Coordinate is:");
point2.display();
System.out.print("The line's length is:");
System.out.println(String.format("%.2f",getDistance()));
}
}
class Plane extends Element{
private String color;
public Plane(){
}
public Plane(String color){
this.color=color;
}
public String getColor(){
return color;
}
public void display(){
System.out.println("The Plane's color is:"+color);
}
}
abstract class Element{
void display(){
}
}
class GeometryObject{
private ArrayList <Element> list = new ArrayList<>();
public GeometryObject()
{
}
public void add(Element element)
{
list.add(element);
}
public void remove(int index)
{
list.remove(index-1);
}
public ArrayList <Element> getList()
{
return list;
}
}
分析:注意index的范围,还是按题目要求写就行。
3.踩坑心得
写四角形时的类没有写好,导致后面写五边形的时候重新写了一遍,五边形的第二个题目没有注意到有六个选项,需要修改正则表达式。使用鞋带定理的时候要先判断点的位置。
期中考试的最后一题没有注意到index的范围,就出现了两个非零返回。
4.改进建议
刚开始写三角形的时候就可以直接构建一个图形类,方便以后使用。还有一些选项的测试点没有通过,可能是算法有问题,还需要改进。
5.总结
在这几周的学习中,老师上课时讲了继承与多态还有抽象类方面的知识。在上课听讲的同时,课后也需要练习,才能掌握这些知识。在java面向对象的学习中,应该多加练习代码,多提高自己的算法能力。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号