CF618E Robot Arm- 计算几何- 线段树

https://www.luogu.com.cn/problem/CF618E
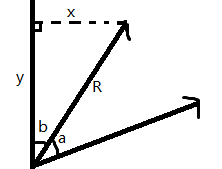
你有一个机械臂，它由 nn 节组成，每一节首尾相接。一开始第i节的起终点为(i-1,0),(i,0)(i−1,0),(i,0)。
有 mm 个操作，操作有两种：
给定 i,li,l,将第 ii 节机械臂沿着原来的方向延长 ll 个单位，其他节与这一节的相对位置不变（见题面图）。
给定 i,\alphai,α,将第 ii 节机械臂以这一节的起点为旋转中心顺时针旋转 \alpha°α° ，其他节与这一节的相对位置不变（见题面图）。
输出每个操作后最后一节的终点的坐标。

---

题解

• 线段树维护多个向量的和（题目所求为n个向量的和）
• 操作1单点修改伸长的向量坐标，线段树单点加法
• 操作2区间修改，标记维护旋转的角度，推一下

向量(x,y)顺时针旋转a的弧度值得到(ycosa + xsina , ycosa - xsina)
证明：
设向量(x,y)的长度为R，与x轴夹角为b，则y=Rcosb，x=Rsinb
由于旋转长度不变，旋转后长度仍为R，夹角为(a+b)，因此
y' = R *cos(a+b) = R *cosa cosb - R *sina sinb = y *cosa - x *sina
x' = R *sin(a+b) = R *sina cosb + R *cosa sinb = y *sina + x *cosa

---

代码

#include <iostream>
#include <cstdio>
#include <cmath>
#include <iomanip>
using namespace std;
const double PI=3.141592653589793;
const int maxn=300003;
int n,m;
struct fdfdfd{int l,r; double endx,endy,ang;}a[maxn<<2];
void pushup(int x) {a[x].endx=a[x<<1].endx+a[x<<1|1].endx; a[x].endy=a[x<<1].endy+a[x<<1|1].endy;}
void pushtag(int x,double d) {
	a[x].ang+=d;
	double tx=a[x].endx,ty=a[x].endy;
	a[x].endx=ty*sin(d)+tx*cos(d),a[x].endy=ty*cos(d)-tx*sin(d);
}
void pushdown(int x) {if(a[x].ang>1e-12) pushtag(x<<1,a[x].ang),pushtag(x<<1|1,a[x].ang),a[x].ang=0;}
void build(int x,int left,int right)
{
	a[x].l=left; a[x].r=right;
	if(left==right) {a[x].endx=1; return;}
	int mid=left+right>>1;
	build(x<<1,left,mid); build(x<<1|1,mid+1,right);
	pushup(x);
}
void query(int x,int d,double &nowx,double &nowy)
{
	if(a[x].l>d||a[x].r<d) return;
	if(a[x].l==d&&a[x].r==d) {nowx=a[x].endx,nowy=a[x].endy; return;}
	pushdown(x);
	query(x<<1,d,nowx,nowy); query(x<<1|1,d,nowx,nowy);
}
void modify_long(int x,int d,double dx,double dy)
{
	if(a[x].l>d||a[x].r<d) return;
	if(a[x].l==d&&a[x].r==d) {a[x].endx+=dx,a[x].endy+=dy; return;}
	pushdown(x);
	modify_long(x<<1,d,dx,dy); modify_long(x<<1|1,d,dx,dy);
	pushup(x);
}
void modify_rot(int x,int left,int right,double d)
{
	if(a[x].l>right||a[x].r<left) return;
	if(left<=a[x].l&&right>=a[x].r) {pushtag(x,d); return;}
	pushdown(x);
	modify_rot(x<<1,left,right,d); modify_rot(x<<1|1,left,right,d);
	pushup(x);
}
int main()
{
	scanf("%d%d",&n,&m); cout<<fixed<<setprecision(10);
	build(1,1,n);
	for(int i=1,t0,t1,t2;i<=m;++i)
	{
		scanf("%d%d%d",&t0,&t1,&t2);
		if(t0==1) {
			double x,y; query(1,t1,x,y);
			modify_long(1,t1,x*t2/sqrt(x*x+y*y),y*t2/sqrt(x*x+y*y));
		}
		else modify_rot(1,t1,n,t2*PI/180.0);
		cout<<a[1].endx<<' '<<a[1].endy<<'\n';
	}
	return 0;
}