有向图的连通性

something important

• 力求描述性语言关键，简练，避免大段文字轰炸
• 部分内容来自网络

---

零.强连通图，强连通分量

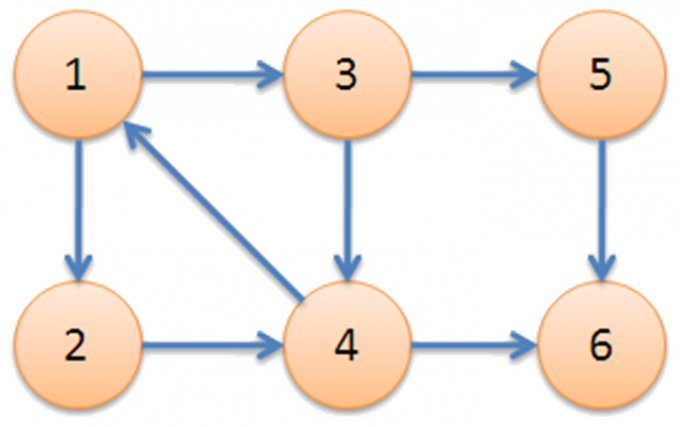
• 强连通图定义：在有向图G中，如果任意两个不同的顶点相互可达，则称该有向图是强连通的。

举个例子：下图有三个子图（强连通分量）：{1,4,5}，{2,3}，

• 求强连通分量的作用：把有向图中具有相同性质的点找出来（求强连通分量），缩点，建立缩图，能够方便地进行其它操作

---

一.floyd算法

算法思想：如果任意两个不同的顶点相互可达，则这两点在同一强连通分量

• 因为效率极低，不常使用，但理解极为简单

//核心代码
for(int k=1;k<=n;++k)//枚举中间点 
	for(int i=1;i<=n;++i)
		for(int j=1;j<=n;++j)
			if(g[i][k]&&g[k][j]) g[i][j]=1;
for(int i=1;i<=n;++i)//计算连通分量数 
{
	if(!vis[i]) vis[i]=++col;
	for(int j=1;j<=n;++j)
		if(g[i][j]==g[j][i]) vis[j]=vis[i];//同属一个连通分量 
}

---

二.Tarjan算法

算法思想：
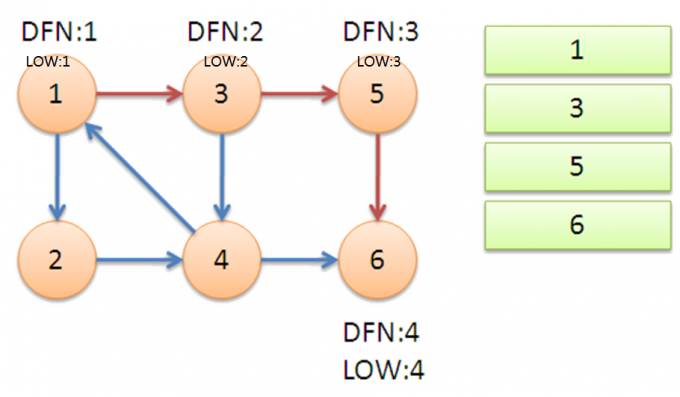
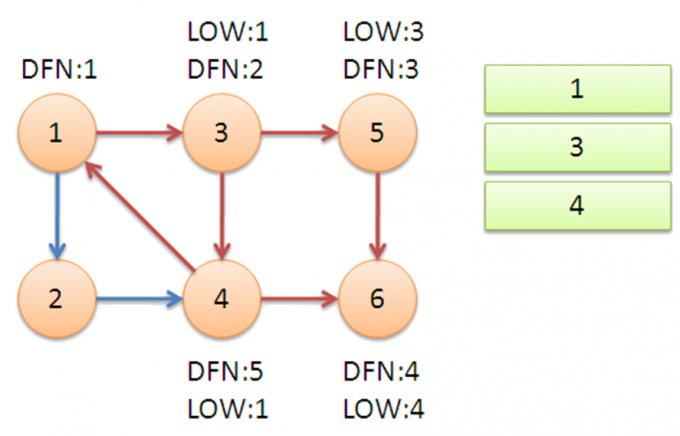
tarjan算法基于对图深度优先搜索，用栈存储整个强连通分量，将每一个强连通分量作为搜索树上的一个子树，而这个图，就是一个完整的搜索树。
DFN[ ]存储点的搜索次序编号，LOW[ ]存储强连通分量（对应搜索树上的一个）子树的根
判断强连通分量：一个点出栈时 DFN==LOW

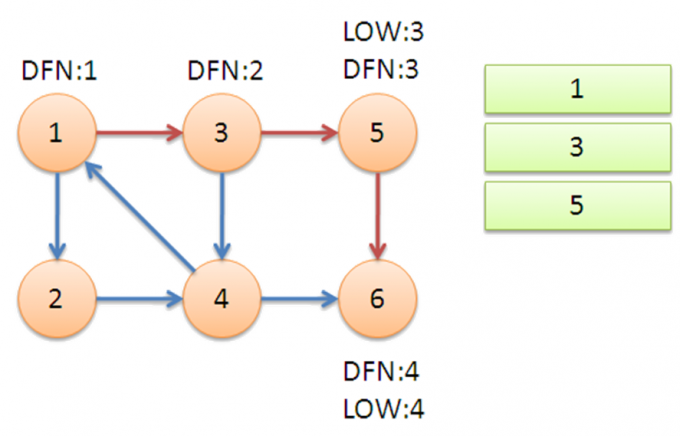
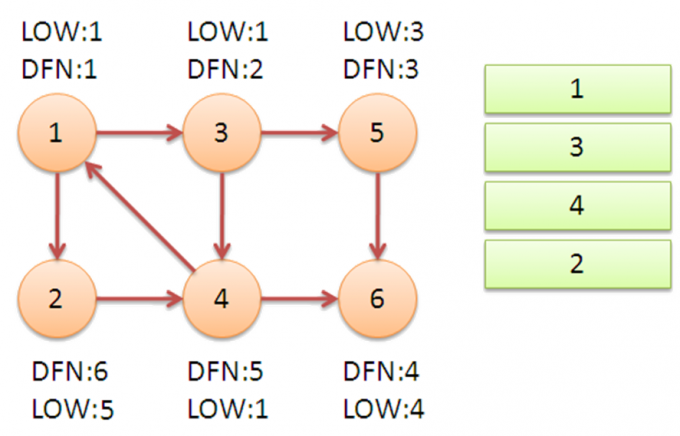
来看一个例子：

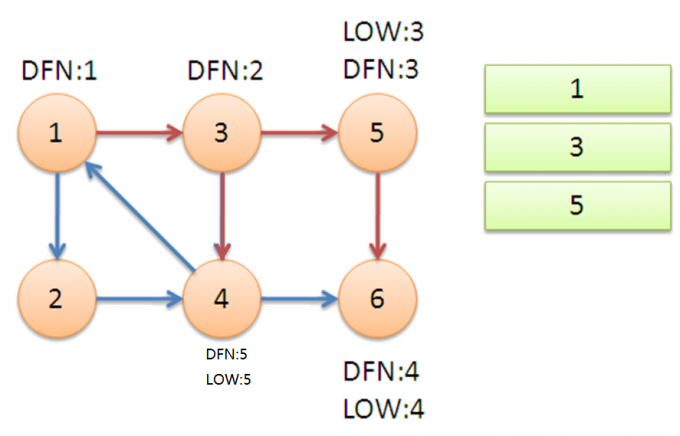
衔接：搜索到1，LOW[4]变为1

//核心代码
void tarjan(int x)
{
	dfn[x]=low[x]=++tot;//新进点的初始化。
	stack[++index]=x;//进栈 
	visit[x]=1;//表示在栈里 
	for(int i=head[x];i;i=e[i].next)
	{
		int v=e[i].to;
		if(!dfn[v])//如果没访问过
		{
			darjan(v);//递归访问 
			low[x]=min(low[x],low[v]);//比较谁是谁的父亲/儿子,父亲相当于强连通分量子树最小根 
		}
		else if(visit[v]) low[x]=min(low[x],dfn[v]);//如果访问过，并且还在栈里。 
	}
	if(low[x]==dfn[x])//是强连通分量子树里的最小根
	{
		++num;//分量数加一 
		do{
			printf("%d ",stack[index]);
			visit[stack[index--]]=0;
		}while(x!=stack[index+1]);
		puts("");
	}
}

运用实例：消息的传递

---

三.Kosaraju算法

算法思想：
Kosaraju算法，基于两次DFS
第一次DFS：对原图进行深度优先遍历，记录每个顶点的离开时间。
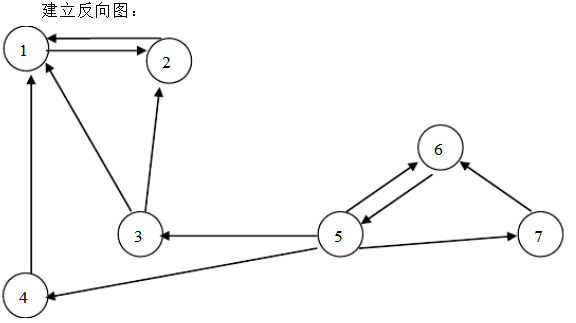
第二次DFS：选择具有最晚离开时间的顶点，对反向图进行深度优先遍历，并标记能够遍历到的顶点，这些顶点构成一个强连通分量

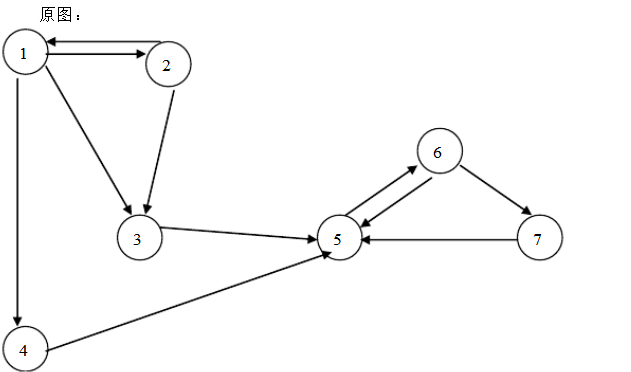
举个栗子：

• 深搜顺序：

• 对原图进行深度优先遍历后，顶点的离开时间分别为：
  1离开时间为7， 4离开时间为6，
  2离开时间为5， 3离开时间为4，
  5离开时间为3， 6离开时间为2，
  7离开时间为1。

• 则按顶点按离开时间从大到小排列的序列为：1、4、2、3、5、6、7，

• 按上述序列对反向图进行深度优先遍历，属于同一次深度优先遍历的顶点则属于同一个强连

• 结果：{1,2}，{3}，{4}，

//核心代码
void dfs1(int x)
{
	vis[x]=1;
	for(int i=head[x];i;i=e[i].next)
	{
		int v=e[i].to;
		if(!vis[i]) dfs1(v);
	}
	stack[++index]=x;
}
void dfs2(int x)
{
	vis[x]=index;
	for(int i=head[x];i;i=e[i].next)
	{
		int v=e[i].to;
		if(!vis[v]) dfs2(i);
	}
}
int main()
{
	for(int i=1;i<=n;++i)
		if(!vis[i]) dfs1(i);
	memset(vis,0,sizeof(vis)); index=0;
	for(int i=1;i>=1;--i)//出栈，连通分量染色
		if(!vis[i]) ++index,dfs2(stack[i]);
}

---

四.总结与对比

Kosaraju算法的优势:

  该算法依次求出的强连通分量已经符合拓扑排序.

Tarjan算法的优势：

  相比Kosaraju算法拥有时间和空间上的巨大优势.

使用范围：

  一般图中选用Tarjan算法，涉及求图的拓扑性质时则选用Kosaraju算法

图片来自百度文库