ML_SVM算法

支持向量机（support vector machine）

背景;

　　深度学*（2012）出现之前，SVM被认为机器学*中*十几年来最成功的，表现最好的算法

机器学*的一般框架;

　　训练集=>提取特征向量=>结合一定的算法（分类器：比如决策树，KNN）=>得到结果

 

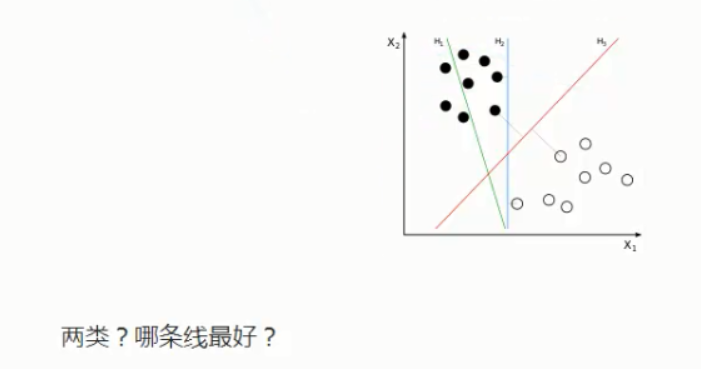
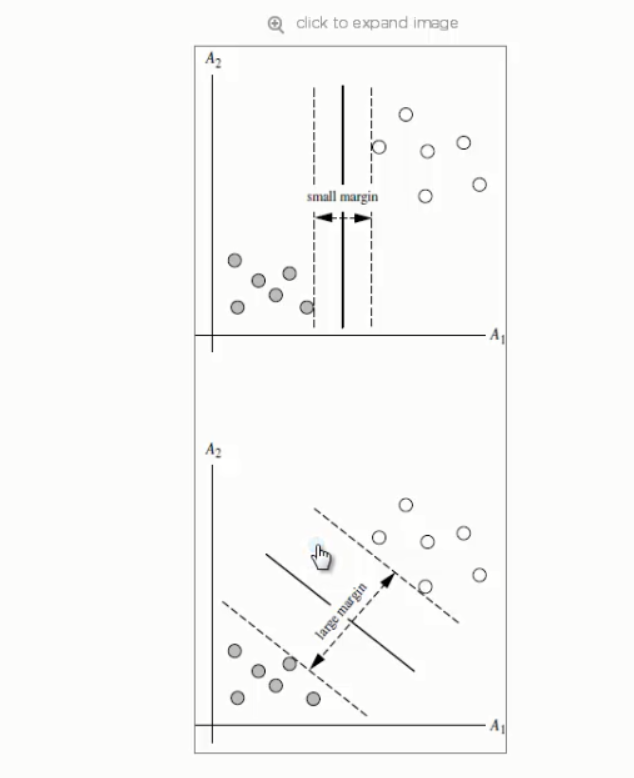
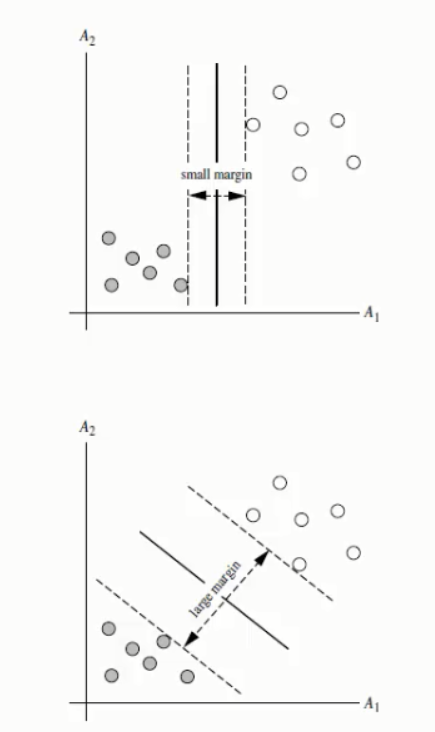
SVM寻找区分两类的超平面（hyper plane）,使边际（margin）最大

　　总共可以有多少个可能的超平面？无数条

　　如何选取使边际（margin）最大的超平面（max margin hyperplane）MMH

　　超平面到一侧最*点的距离等于到另一侧最*点点的距离，两侧的两个超平面平行

线性可区分（linear separable）和线性不可区分（linear inseparable）

定义与公式建立

　　超平面可以定义为：

　　　

n是特征值的个数

　　　　X：训练实例

　　　　b：bias偏向

假设2维特征向量：X=（X1,X2）

把b想象成额外的weight

超平面方程变为：

　　　　　　　　　　　　　

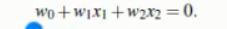
所有超平面右上方的点满足;

   　　　　　　　　　　　

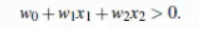
所有超平面左下方的点满足;

　　　　　　　　　　　　

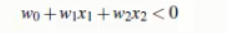
　　调整weight，使超平面定义边际的两边;

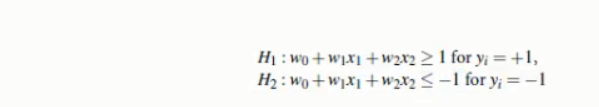
　　综合以上两式，得到;(1)

 

　　所有坐落在边际的两边的超平面上的点被称作“支持向量（support vectors）”

　　分界的超平面和H1或H2上任意一点的距离为

 

SVM如何找出最大边际的超平面呢（MMH）?

　　

 

　　　　　

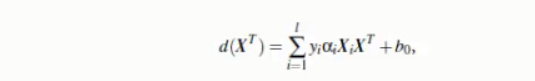
其中，yi是支持向量点X_i的类别标记　　　　X^T是要测试的实例

　　l是支持向量点的个数

　　根据得出符号的正负决定测试实例的归类

 

 

 

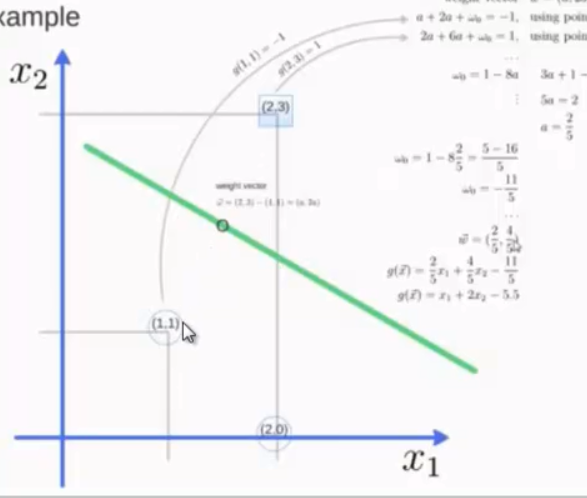
from sklearn import svm

x=[[2,0],[1,1],[2,3]]
y=[0,0,1]           #向量点的类别标记
clf=svm.SVC(kernel='linear')
clf.fit(x,y)           #算出超平面，保存在clf

print clf

#get support vectors
print clf.support_vectors

#get indices of support vectors   索引
print clf.support_

#get number of support vectors for each class
print clf.n_suppoart_

print clf.predict([2,0])

 

　

　

import numpy as np
import pylab   as pl
from sklearn import svm

#we creat 40 separable points 
np.random.seed(0)                     #让下次还随机产生同样的点
x=np.r_[np.random.randn(20,2)-[2,2],np.random.randn（20,2）+[2,2]]
y=[0]*20+[1]*20            

#fit the model
clf=svm.SVC(kernel='linear')
clf.fit(x,y)           #算出超平面，保存在clf

#get the separating hyperplane
w=clf.coef_[0]
a=-w[0]/w[1]         #直线的斜率
xx=np.linspace(-5,5)  #从-5到5产生连续的x的值
yy=a*xx-(clf.intercept_[0])/w[1]


#plot the parallels to the separating hyperplane that pass through the support vectors
b=clf.support_vectors[0]
yy_down=a*xx+(b[1]-a*b[0])
b=clf.support_vectors[-1]
yy_up=a*xx+(b[1]-a*b[0])


print "w: ",w
print "a: ",a
print "support_vectors_： ”，clf.support_vectors_
print "clf.coef_； ”，clf.coef_



#plot the line,the points, and the nearest vectors to the plane
pl.plot(xx,yy,'k-')
pl.plot(xx,yy_down,'k--')
pl.plot(xx,yy_up,'k--')

pl.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],
               s=80,facecolors='none')
pl.scatter(x[:. 0],x[:, 1],c=Y,cmap=pl.cm.paired)

pl.ais('tight')
pl.show（）
        

 

SVM算法下:

1.1 训练好的模型的算法复杂度是由支持向量的个数决定的，而不是由数据的维度决定的。所以SVM不太容易产生overfitting

1.2 SVM训练出的模型完全依赖于支持向量，即使训练集里面所有非支持向量的点都被去除，重复训练过程，结果仍然会得到完全一样的模型。

1.3 一个SVM如果训练得出得支持向量个数比较小，SVM训练出的模型比较容易被泛化。

2. 线性不可分的情况（linearly inseparable case）

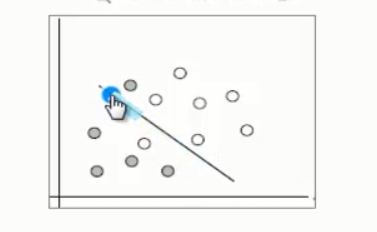
2.1 数据集在空间中对应的向量不可被一个超平面区分开

2.2 两个步骤来解决：

　　2.2.1 利用一个非线性的映射把原数据集中的向量点转化到一个更高维度的空间中

　　2.2.2 在这个高维度的空间中找一个线性的超平面来根据线性可分的情况处理

 

 

4. SVM扩展可解决多个类别分类问题

　　对于每个类，有一个当前类和其他类的二类分类器（one-vs-rest）