1、、关于栈和双链表的基础知识

1、、关于栈和双链表的基础知识

一、利用栈来解决逆波兰表达式

1、后缀表达式求值

后缀表达式也叫逆波兰表达式，其求值过程可以用到栈来辅助存储。假定待求值的后缀表达式为：6 5 2 3 + 8 * + 3 + *，则其求值过程如下：

1）遍历表达式，遇到的数字首先放入栈中，此时栈如下所示：

2）接着读到“+”，则弹出3和2，执行3+2，计算结果等于5，并将5压入到栈中。

3）读到8，将其直接放入栈中。

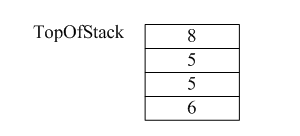
4）读到“”，弹出8和5，执行85，并将结果40压入栈中。而后过程类似，读到“+”，将40和5弹出，将40+5的结果45压入栈...以此类推。最后求的值288。

2、中缀表达式转后缀表达式

2.1）规则
中缀表达式a + b*c + (d * e + f) * g，其转换成后缀表达式则为a b c * + d e * f + g * +。

转换过程需要用到栈，具体过程如下：

1）如果遇到操作数，我们就直接将其输出。

2）如果遇到操作符，则我们将其放入到栈中，遇到左括号时我们也将其放入栈中。

3）如果遇到一个右括号，则将栈元素弹出，将弹出的操作符输出直到遇到左括号为止。注意，左括号只弹出并不输出。

4）如果遇到任何其他的操作符，如（“+”， “*”，“（”）等，从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为止。弹出完这些元素后，才将遇到的操作符压入到栈中。有一点需要注意，只有在遇到" ) "的情况下我们才弹出" ( "，其他情况我们都不会弹出" ( "。

5）如果我们读到了输入的末尾，则将栈中所有元素依次弹出。

2.2）实例
规则很多，还是用实例比较容易说清楚整个过程。以上面的转换为例，输入为a + b * c + (d * e + f)*g，处理过程如下：

1）首先读到a，直接输出。

2）读到“+”，将其放入到栈中。

3）读到b，直接输出。

此时栈和输出的情况如下：

4）读到“*”，因为栈顶元素"+"优先级比" * " 低，所以将" * "直接压入栈中。

5）读到c，直接输出。

此时栈和输出情况如下：

6）读到" + "，因为栈顶元素" * "的优先级比它高，所以弹出" * "并输出， 同理，栈中下一个元素" + "优先级与读到的操作符" + "一样，所以也要弹出并输出。然后再将读到的" + "压入栈中。

此时栈和输出情况如下：

7）下一个读到的为"("，它优先级最高，所以直接放入到栈中。

8）读到d，将其直接输出。

此时栈和输出情况如下：

9）读到" * "，由于只有遇到" ) "的时候左括号"("才会弹出，所以" * "直接压入栈中。

10）读到e，直接输出。
此时栈和输出情况如下：

11）读到" + "，弹出" * "并输出，然后将"+"压入栈中。

12）读到f，直接输出。

此时栈和输出情况：

13）接下来读到“）”，则直接将栈中元素弹出并输出直到遇到"("为止。这里右括号前只有一个操作符"+"被弹出并输出。

14）读到" * "，压入栈中。读到g，直接输出。

15）此时输入数据已经读到末尾，栈中还有两个操作符“*”和" + "，直接弹出并输出。

3、实例

后缀表达式计算 (100 分)

Kunkun学长觉得应该让学弟学妹了解一下这个知识点：后缀表达式相对于中缀表达式更容易让计算机理解和学习。现在kunkun学长给出一串后缀表达式，你能帮他算出这个后缀表达式的值吗？

输入格式:

第一行输入后缀表达式长度n（1<=n<=25000）；

第二行输入一个字符串表示后缀表达式（每个数据或者符号之间用逗号隔开，保证输入的后缀表达式合法，每个数包括中间结果保证不超过long long长整型范围）

输出格式:

输出一个整数，即后缀表达式的值。

输入样例1:

6
10,2,+

输出样例1:

12

输入样例2:

14
2,10,2,+,6,/,-

输出样例2:

0

代码实现：

#include<iostream>

#include<math.h>

#include<vector>

using namespace std;

int main(){
	int n;
	long long int temp;
	string a;
	cin >> n >> a;
	vector<long long int> A;
	int begin = 0, end = 0;
	for(int i = 0; i < n; i ++ ){
		if(a[i] == ',' || i == n - 1){
			end = i - (i != n - 1);
			int cnt = end - begin + 1;
			if(cnt == 1 && a[begin] < '0'){
				if(a[begin] == '+'){
					temp = A[A.size() - 2] + A[A.size() - 1];
					A.pop_back();
					A.pop_back();
					A.push_back(temp);
				}
				if(a[begin] == '-'){
					temp = A[A.size() - 2] - A[A.size() - 1];
					A.pop_back();
					A.pop_back();
					A.push_back(temp);
				}
				if(a[begin] == '*'){
					temp = A[A.size() - 2] * A[A.size() - 1];
					A.pop_back();
					A.pop_back();
					A.push_back(temp);
				}
				if(a[begin] == '/'){
					temp = A[A.size() - 2] / A[A.size() - 1];
					A.pop_back();
					A.pop_back();
					A.push_back(temp);
				}
				begin += 2;
				continue;
			}
			temp = 0; 
			for(int j = begin; j <= end; j ++){
				if(a[j] == '-'){
					cnt --;
					continue;
				}
				else{
					temp += (a[j] - '0') * pow(10, cnt - 1);
					cnt --;
				}
			}
			if(a[begin] == '-') temp *= -1;
			begin = i + 1;
			A.push_back(temp);
		}
	}
	cout << A[0];
	return 0;
}

二、利用数组来模拟双链表

数组实现双链表比单链表就多了一些对于左指针的操作。
为了实现的方便，不像在单链表实现里用一个额外的变量head去记录链表的头节点。
而是直接用两个哨兵节点固定为双链表的头节点和尾节点。
我们可以固定头节点为0，尾节点为1.

也就是说，0的right指针指向链表的第一个节点，1的left指针指向链表的第一个节点。
这样，0和1就被固定为头节点和尾节点了。我们如果要插入节点，初始下标就得从2开始。

类比单链表的数组实现，要实现双链表，就得开三个数组val，l，r。
val[i]表示下标为i的节点的值，l[i]表示下标为i的节点的前驱节点，r[i]表示下标为i的节点的后继结点。

另外还需要有一个变量idx记录当前插入的节点的下标。由于0和1已经被占用了，所以idx从2开始。

用几张图来模拟一下双链表的一些操作：

初始化

k右边插入一个数

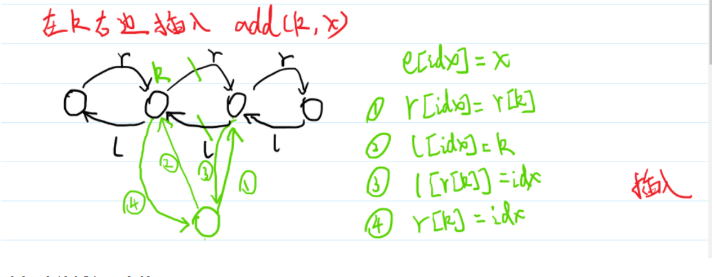
对应k左边插入一个数

删除第K个点

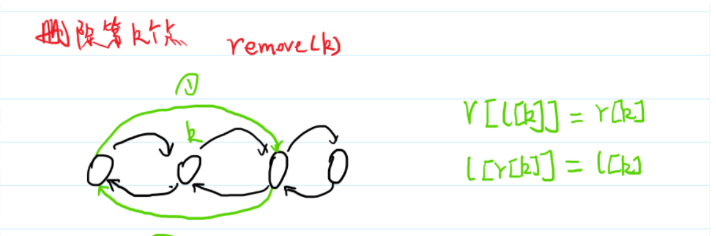
来看个实例题目链接在这

这道题的题意是要我们实现一个双链表，双链表支持五个操作：
（1）在链表的第一个节点之前（最左侧）插入一个数
（2）在链表的最后一个节点之后（最右侧）插入一个数
（3）删除第k个插入的数
（4）在第k个插入的数左侧插入一个数
（5）在第k个插入的数右侧插入一个数

双链表一些基本操作对应的函数代码：

初始化

void init()
{
    l[1] = 0;
    r[0] = 1;
    index = 2;
} 

这三行代码的作用是初始化一个空的双链表，头节点0的right指针指向尾节点1，尾节点1的left指针指向头节点0，要插入的数的下标初始化为2（因为0，1已经被占用了）。

k右边插入一个数

void add(int k, int x)
{
    e[index] = x;
    l[index] = k;
    r[index] = r[k];
    l[r[k]] = index;
    r[k] = index++;
}

步骤如下：

1.首先需要创建一个含有值x的节点：e[idx] = x;
然后这个点的右指针要指向下标为k的点的右指针指向的节点，这个点的左指针要指向下标为k的点。

2.修改原来的两个节点，下标为k的节点的右指针指向这个新插入的节点，还有原来是下标为k的节点的下一个节点的左指针要指向新插入的节点。

3.修改了指针之后，下标idx要增加，以便之后插入新的节点。

对应k左边插入一个数

add(l[k], x);

删除第K个点

要删除下标为k的节点，只需要让它的前驱节点的右指针指向它的后继结点，它的后继结点的左指针指向它的前驱节点。

void remove(int k)
{
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}

上代码：

#include<bits/stdc++.h>

using namespace std;

const int N = 100010;

int l[N],r[N],e[N],idx;

void init(){
    r[0] = 1;
    l[1] = 0;
    idx = 2;
}

void add(int k, int x){
    e[idx] = x;
    l[idx] = k;
    r[idx] = r[k];
    l[r[k]] = idx;
    r[k] = idx ++;
}

void remove(int k){
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}

int main(){
    init();
    int k, x, m;
    string op;
    cin >> m;
    while(m --){
        cin >> op;
        if(op == "L"){
            cin >> x;
            add(0, x);
        }
        if(op == "R"){
            cin >> x;
            add(l[1], x);
        }
        if(op == "D"){
            cin >> k;
            remove(k + 1);
        }
        if(op == "IL"){
            cin >> k >> x;
            add(l[k + 1], x);
        }
        if(op == "IR"){
            cin >> k >> x;
            add(k + 1, x);
        }
    }
    for(int i = r[0]; i != 1; i = r[i]) cout << e[i] << ' ';
    return 0;
}