A Very Simple Problem

A Very Simple Problem

Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 88 Accepted Submission(s): 55

Problem Description

This is a very simple problem. Given three integers N, x, and M, your task is to calculate out the following value:

 

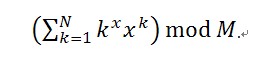Input

There are several test cases. For each case, there is a line with three integers N, x, and M, where 1 ≤ N, M ≤ 2*10⁹, and 1 ≤ x ≤ 50.
The input ends up with three negative numbers, which should not be processed as a case.

 

Output

            For each test case, print a line with an integer indicating the result.

 

Sample Input

100 1 10000
3 4 1000
-1 -1 -1

 

Sample Output

5050
444

 

Source

2010 ACM-ICPC Multi-University Training Contest（5）——Host by BJTU

 

Recommend

zhengfeng

 

/*
题意：给你n，x，m，让你求1^x*x^1+2^x*x^2+...+n^x*x^n;

初步思路：刚开始一点思路也没有，看了题解才发现妙处。

#补充：设F[n]=x^n,n*(x^n),(n^2)*(x^n),...,(n^x)*(x^n);
       得到：
         F[n][k]=(n^k)*(x^n);
       则要求的结果为：
         G[n]=F[1][k]+F[2][k]+...+F[n][k];
       设C(i,j)为组合数，即i种元素取j种的方法数 
       所以有：f[n+1][k] = ((n+1)^k)*(x^(n+1)) （二次多项式展开）
                         = x*( C(k,0)*(x^n)+C(k,1)*n*(x^n)+...+C(k,k)*(n^k)*(x^n) ) 
                         = x*( C(k,0)*f[n][0]+C(k,1)*f[n][1]+...+C(k,k)*f[n][k] ) 
       得到递推式就可以用矩阵进行快速幂求解
        |x*1 0................................0|       |f[n][0]|       |f[n+1][0]| 
        |x*1 x*1 0............................0|       |f[n][1]|       |f[n+1][1]| 
        |x*1 x*2 x*1 0........................0|   *   |f[n][2]|   =   |f[n+1][2]| 
        |......................................|       |.......|       |.........| 
        |x*1 x*C(k,1) x*C(k,2)...x*C(k,x) 0...0|       |f[n][k]|       |f[n+1][k]| 
        |......................................|       |.......|       |.........| 
        |x*1 x*C(x,1) x*C(x,2).......x*C(x,x) 0|       |f[n][x]|       |f[n+1][x]| 
        |0................................0 1 1|       |g[n-1] |       | g[ n ]  | 
*/
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,x,mod;
ll c[55][55];
ll unit;
/********************************矩阵模板**********************************/
class Matrix {
    public:
        ll a[55][55];
        int n;
        void init() {
            memset(a,0,sizeof(a));//            #出错
            for(int i=0;i<=n;i++){
                for(int j=0;j<=i;j++){
                    a[i][j]=x*c[i][j]%mod;
                }
            }
            a[x+1][x]=a[x+1][x+1]=1;
        }
        Matrix operator +(Matrix b) {
            Matrix c;
            c.n = n;
            for (int i = 0; i < n; i++)
                for (int j = 0; j < n; j++)
                    c.a[i][j] = (a[i][j] + b.a[i][j]) % mod;
            return c;
        }

        Matrix operator +(int x) {
            Matrix c = *this;
            for (int i = 0; i < n; i++)
                c.a[i][i] += x;
            return c;
        }

        Matrix operator *(Matrix b)
        {
            Matrix p;
            p.n = b.n;   
            memset(p.a,0,sizeof p.a);
            for (int i = 0; i < n; i++)
                for (int j = 0; j < n; j++)
                for (int k = 0; k < n; k++)
                    p.a[i][j] = (p.a[i][j] + (a[i][k]*b.a[k][j])%mod) % mod;
            return p;
        }

        Matrix power(int t) {
            Matrix ans,p = *this;
            ans.n = p.n;  
            memset(ans.a,0,sizeof ans.a);
            for(int i=0;i<=n;i++){//初始化ans
                ans.a[i][i]=1;
            }
            while (t) {
                if (t & 1)
                    ans=ans*p;
                p = p*p;
                t >>= 1;
            }
            return ans;
        }
}init;
void Init(){//求组合数
    memset(c,0,sizeof c);
    for(ll i=0;i<=x;i++)  
            c[i][0]=c[i][i]=1;  
    for(ll i=2;i<=x;i++)  
        for(ll j=1;j<i;j++)  
            c[i][j]=((ll)c[i-1][j-1]+c[i-1][j])%mod;
    unit=0;
}
/********************************矩阵模板**********************************/
int main(){
    // freopen("in.txt","r",stdin);
    while(scanf("%lld%lld%lld",&n,&x,&mod)!=EOF&&(n>0,x>0,mod>0)){
        Init();//                #ok
        
        // for(int i=0;i<=x;i++){
            // for(int j=0;j<=x;j++){
                // cout<<c[i][j]<<" ";
            // }
            // cout<<endl;
        // }
        // cout<<endl;
        
        init.n=x+2;
        // cout<<"ok"<<endl;
        init.init();
        
        // for(int i=0;i<=x+1;i++){
            // for(int j=0;j<=x+1;j++){
                // cout<<init.a[i][j]<<" ";
            // }cout<<endl;
        // }
        
        // cout<<"ok"<<endl;
        init=init.power(n);
        
        // for(int i=0;i<=x+1;i++){
            // for(int j=0;j<=x+1;j++){
                // cout<<init.a[i][j]<<" ";
            // }cout<<endl;
        // }
        
        for(int i=0;i<=x;i++){
            unit+=( (x*init.a[x+1][i])%mod );
        }
        printf("%lld\n",(unit+mod)%mod);
    }
    return 0;
}