Fibonacci Check-up

Fibonacci Check-up

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 42 Accepted Submission(s): 27

Problem Description

Every ALPC has his own alpc-number just like alpc12, alpc55, alpc62 etc.
As more and more fresh man join us. How to number them? And how to avoid their alpc-number conflicted?
Of course, we can number them one by one, but that’s too bored! So ALPCs use another method called Fibonacci Check-up in spite of collision.

First you should multiply all digit of your studying number to get a number n (maybe huge).
Then use Fibonacci Check-up!
Fibonacci sequence is well-known to everyone. People define Fibonacci sequence as follows: F(0) = 0, F(1) = 1. F(n) = F(n-1) + F(n-2), n>=2. It’s easy for us to calculate F(n) mod m.
But in this method we make the problem has more challenge. We calculate the formula 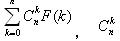, is the combination number. The answer mod m (the total number of alpc team members) is just your alpc-number.

 

Input

First line is the testcase T.
Following T lines, each line is two integers n, m ( 0<= n <= 10^9, 1 <= m <= 30000 )

 

Output

Output the alpc-number.

 

Sample Input

2
1 30000
2 30000

 

Sample Output

1
3

 

Source

2009 Multi-University Training Contest 5 - Host by NUDT

 

Recommend

gaojie

 

/*
题意：给出你公式，让你求( 求和C(k,n)F(k) )%m

初步思路：没思路，先打表
            得到：
            0
            1
            3
            8
            21
            55
            144
            377
            987
            2584
            6765
            17711
            46368
            121393
            317811
            832040
            2178309
            5702887
            14930352
            39088169
            102334155
            能得出来，G(0)=0;
                      G(1)=1;
                      G(n)=3*G(n-1)-G(n-2);
            然后用矩阵快速幂求出结果
            
            最重要的构造矩阵还没学线性代数的我只能试着推出来：
            |G(n) G(n-1)| | 3     1   |
            | 0    0    |*| -1    0   |

#总结：板没调好，WA了两发
            
*/
#include<bits/stdc++.h>
using namespace std;
int n,mod;
int t;
/********************************矩阵模板**********************************/
class Matrix {
    public:
        int a[3][3];
        int n;  

        void init(int x) {
            memset(a,0,sizeof(a));
            if(x){
                a[0][0]=3;
                a[0][1]=1;
                a[1][0]=-1;
                a[1][1]=0;
            }else{
                a[0][0]=1;
                a[0][1]=0;
                a[1][0]=0;
                a[1][1]=0;
            }
            n=2;
        }

        Matrix operator +(Matrix b) {
            Matrix c;
            c.n = n;
            for (int i = 0; i < n; i++)
                for (int j = 0; j < n; j++)
                    c.a[i][j] = (a[i][j] + b.a[i][j]) % mod;
            return c;
        }

        Matrix operator +(int x) {
            Matrix c = *this;
            for (int i = 0; i < n; i++)
                c.a[i][i] += x;
            return c;
        }

        Matrix operator *(Matrix b)
        {
            Matrix p;
            p.n = b.n;   
            memset(p.a,0,sizeof p.a);
            for (int i = 0; i < n; i++)
                for (int j = 0; j < n; j++)
                for (int k = 0; k < n; k++)
                    p.a[i][j] = (p.a[i][j] + (a[i][k]*b.a[k][j])%mod) % mod;
            return p;
        }

        Matrix power_1(int t) {
            Matrix ans,p = *this;
            ans = p;
            while (t) {
                if (t & 1)
                    ans=ans*p;
                p = p*p;
                t >>= 1;
            }
            return ans;
        }
        
        Matrix power_2(Matrix a,Matrix b,int x){
            while(x){
                if(x&1){
                    b=a*b;
                }
                a=a*a;
                x>>=1;
            }
            return b;
        }
};
/********************************矩阵模板**********************************/
Matrix unit,init;
int main(){
    // freopen("in.txt","r",stdin);
    scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&mod);
        unit.init(0);//存放G(n)的矩阵
        init.init(1);//子矩阵
        if(n==0){
            printf("0\n");
            continue;
        }else if(n==1){
            printf("%d\n",1%mod);
            continue;
        }
        init=init.power_1(n-2);
        unit=unit*init;
        // cout<<mod<<endl;
        // for(int i=0;i<2;i++){
            // for(int j=0;j<2;j++){
                // cout<<init.a[i][j]<<" ";
            // }
            // cout<<endl;
        // }
        
        printf("%d\n",(unit.a[0][0]+mod)%mod);
    }
    return 0;
}

/*
附上打表小程序
*/
#include<bits/stdc++.h>
using namespace std;
long long Sums(long long n,long long k) //函数定义
{
    long long sum = 0,N=1,K=1,M=1;
    if(k > 0 && k<=n)
    {
        for(long long i = 1;i<=n;i++)
        {
            N = N * i;
        }
 
        for(long long j = 1;j <= k;j++)
        {
            K = K * j;
        }
 
        for(long long h = 1;h <= n-k;h++)
        {
            M = M * h;
        }
        sum=N/(K*M);
        return sum;
    }
    else    
        return 0;
}
int main(){
    //freopen("in.txt","r",stdin);
    long long f[25];
    f[0]=0;
    f[1]=1;
    for(long long i=2;i<=20;i++)
        f[i]=f[i-1]+f[i-2];
    for(long long n=0;n<=20;n++){
        long long cur=0;
        for(long long k=0;k<=n;k++){
            long long cnk=Sums(n,k);
            //cout<<"C("<<k<<","<<n<<")="<<cnk<<endl;
            cur+=cnk*f[k];
        }
        cout<<cur<<endl;
    }
    return 0;
}